नमूना डेटा से मांग की मूल्य लोच की गणना

आपके द्वारा उपलब्ध कराए गए मूल्य और मांग की मात्रा के नमूना आंकड़ों के आधार पर मांग की मूल्य लोच का अनुमान लगाने के लिए इस कैलकुलेटर का उपयोग करें।

आपको दोनों नमूनों (कीमत और माँगी गई मात्रा) के सकारात्मक मान के संदर्भ में वैध नमूना डेटा प्रदान करना होगा। एक बार जब आप अपना डेटा स्प्रेडशीट में चिपका देते हैं, तो आप दिखाए गए सभी चरणों को प्राप्त करने के लिए "गणना करें" पर क्लिक कर सकते हैं।

ध्यान दें कि इस दृष्टिकोण के लिए डेटा को एक विशिष्ट पैटर्न का पालन करने की आवश्यकता होती है जो लॉग-लॉग मॉडल के अनुकूल होता है, जहां \(\ln(P)\) और \(\ln(Q)\) को रैखिक प्रतिगमन मॉडल का संचालन करने के लिए सहायक चर के रूप में उपयोग किया जाता है।

नमूना डेटा से मूल्य लोच की गणना

मूल्य लोच की गणना करने के लिए, आपको निम्नलिखित सहायक मॉडल का अनुमान लगाना होगा:

\[\displaystyle \ln(Q) = a + b \ln(P) \]

ध्यान दें कि यह एक नियमित रैखिक प्रतिगमन मॉडल के अनुरूप है जिसमें मूल चर मूल्य और मात्रा लॉग-रूपांतरित हैं। यही कारण है कि हमें दोनों चरों को सख्ती से सकारात्मक होने की आवश्यकता है।

लोच की गणना के चरण क्या हैं?

• स्टेप 1: मूल्य (P) और मात्रा (Q) के लिए दिए गए चरों के लिए नमूना डेटा की पहचान करें
• चरण दो: सुनिश्चित करें कि दोनों नमूनों का नमूना आकार समान हो और वे दोनों सकारात्मक हों, अन्यथा आप गणना नहीं कर पाएंगे
• चरण 3: दोनों चरों का लॉग-रूपांतरण: ln(X) और ln(Y) की गणना करें
• चरण 4: चर ln(X) और ln(Y) के लिए एक सहायक रैखिक प्रतिगमन का संचालन करें, जहाँ ln(X) स्वतंत्र चर है और ln(Y) आश्रित चर है
• चरण 5: इस सहायक प्रतिगमन के लिए पाया गया ढलान गुणांक इन आंकड़ों के लिए मांग की कीमत लोच है

फिर महत्वपूर्ण चरण डेटा का लॉग-रूपांतरण है, जो हमें रैखिक प्रतिगमन के परिणामों के आधार पर लोच की गणना करने की अनुमति देता है, जिससे प्राप्त परिणाम अत्यधिक व्याख्या योग्य हो जाते हैं।

मूल्य लोच को समझना

परिभाषा के अनुसार, मूल्य लोच को निम्नलिखित सूत्र का उपयोग करके परिभाषित किया जाता है:

\[ \varepsilon = \displaystyle \frac{\% \Delta Q }{\% \Delta P} \]

यह इंगित करता है कि, अन्य बातों के अलावा, हम निम्नलिखित अभिव्यक्ति का उपयोग करके मात्रा मांग के प्रतिशत परिवर्तन की भविष्यवाणी कर सकते हैं:

\[ \% \Delta Q = \varepsilon \cdot \% \Delta P \]

यह दर्शाता है कि Q में प्रतिशत परिवर्तन P में प्रतिशत परिवर्तन के समान है जिसे लोच से गुणा किया जाता है। यह ध्यान रखना महत्वपूर्ण है कि यह परिभाषा लागू होती है बिन्दुवार : इसका मतलब यह है कि लोच को पूरे मांग वक्र में स्थिर नहीं रहना चाहिए। हालाँकि यह हो सकता है, और इस कैलकुलेटर में ऐसी धारणा बनाई गई है।

मूल्य लोच गुणांक की व्याख्या

जैसा कि हमने पिछले अनुभाग में देखा, लोच \(\varepsilon\) केवल सहायक लॉग-रूपांतरित प्रतिगमन के ढलान गुणांक के अनुरूप है। लेकिन साथ ही, इसकी एक बहुत ही दिलचस्प सीमांत परिवर्तन व्याख्या है:

• कीमत में अतिरिक्त 1% परिवर्तन के लिए, मात्रा की मांग \(\varepsilon \%\) से बदल जाती है

यह वही है जो लोच सूत्र द्वारा अपेक्षित और निहित है। ध्यान दें कि यह कैलकुलेटर एक मॉडल का अनुमान लगाता है जो मानता है कि डेटा एक ऐसे पैटर्न का अनुसरण करता है जो एक स्थिर लोच के लिए अनुकूल है, जो कि एक रैखिक मांग फ़ंक्शन के मामले में नहीं है, उदाहरण के लिए।

मूल्य लोच को प्रभावित करने वाले कारक

लोच, कीमत में होने वाले बदलावों के प्रति उपभोक्ताओं की प्रतिक्रिया का प्रतिबिंब है। आमतौर पर, लोच नकारात्मक होती है: यदि किसी वस्तु की कीमत बढ़ जाती है, तो खरीदार संभवतः कम खरीदेगा, कम से कम अगर हमारे पास सामान्य वस्तु है।

निरपेक्ष मूल्य में 1 से अधिक (-1 से कम) लोच को कीमत के प्रति लोचदार प्रतिक्रिया से संबद्ध कहा जाता है, जबकि निरपेक्ष मूल्य में 0 और 1 के बीच (-1 और 0 के बीच) लोच को कीमत के प्रति अलोचदार प्रतिक्रिया से संबद्ध कहा जाता है।

अर्थशास्त्र का सिद्धांत भविष्यवाणी करता है कि मांग की कीमत लोच को विभिन्न कारक प्रभावित करेंगे। उदाहरण के लिए, विकल्पों की अनुपस्थिति या कमी से निरपेक्ष मूल्यों में अधिक लोच पैदा होगी।

नमूना लोच गणना: नमूना डेटा का उपयोग करना

निम्नलिखित नमूना डेटा से लोच की गणना करें:

पी	क्यू
1	10
2	13.4
3	15.8
4	21.2
5	26.7
6	40.1

समाधान इन आंकड़ों से मांग की कीमत लोच का पता लगाने के लिए, हमें एक लॉग-लॉग प्रतिगमन मॉडल बनाने की आवश्यकता है, जहां स्वतंत्र चर जिसका हम उपयोग करेंगे वह \(ln(P)\) है, और आश्रित चर \(ln(Q)\) का प्राकृतिक लॉग है

इस सहायक प्रतिगमन के लिए प्रतिगमन गुणांक की गणना करने के लिए, निम्नलिखित तालिका का उपयोग करना आवश्यक है:

	पी	जेड = एलएन(पी)	क्यू	डब्ल्यू = एलएन(क्यू)	\(Z \cdot W\)	\(Z^2\)	\(W^2\)
	1	0	10	2.303	0	0	5.302
	2	0.69	13.4	2.595	1.8	0.48	6.735
	3	1.1	15.8	2.76	3.03	1.21	7.618
	4	1.39	21.2	3.054	4.23	1.92	9.327
	5	1.61	26.7	3.285	5.29	2.59	10.789
	6	1.79	40.1	3.691	6.61	3.21	13.626
Sum =	21	6.58	127.2	17.688	20.97	9.41	53.397

उपरोक्त तालिका के आधार पर निम्नलिखित की गणना की जाती है:

\[\bar Z = \frac{1}{n} \sum_{i=1}^{n} Z_i = \frac{ 6.579}{ 6} = 1.097\]\[\bar W = \frac{1}{n} \sum_{i=1}^{n} Y_i = \frac{ 17.688}{ 6} = 2.948\] \[\large SS_{ZZ} = \sum_{i=1}^{n} Z_i^2 - \displaystyle\frac{1}{n}\left(\sum_{i=1}^{n} Z_i\right)^2 = 9.41 - 6.579^2/6 = 2.195\] \[\large SS_{WW} = \sum_{i=1}^{n} W_i^2 - \displaystyle\frac{1}{n}\left(\sum_{i=1}^{n} W_i\right)^2 = 53.397 - 17.688^2/6 = 1.254\] \[\large SS_{ZW} = \sum_{i=1}^{n} Z_i W_i - \displaystyle\frac{1}{n}\left(\sum_{i=1}^{n} Z_i\right) \left(\sum_{i=1}^{n} W_i\right) = 20.965 - 6.579 \times 17.688/6 = 1.57\]

इसलिए, उपरोक्त गणनाओं के आधार पर, प्रतिगमन गुणांक (ढलान \(m\), और y-अवरोधन \(n\)) निम्नानुसार प्राप्त किए जाते हैं:

\[m = \frac{SS_{ZW}}{SS_{ZZ}} = \frac{ 1.57}{ 2.195} = 0.715\]\[n = \bar W - \bar Z \cdot m = 2.948 - 1.097 \times 0.715 = 2.1639\]

इसलिए, हम पाते हैं कि प्रतिगमन समीकरण है:

\[W = 2.1639 + 0.715 \text{ Z}\]

लेकिन चूंकि सहायक चर \(Z = \ln(X)\) और \(W = \ln(Y)\) हैं, हम निष्कर्ष निकालते हैं कि लॉग-लॉग प्रतिगमन समीकरण है:

\[\ln(Q) = 2.1639 + 0.715 \ln(P)\]

इसलिए, ऊपर दी गई जानकारी के आधार पर, निम्नलिखित स्कैटर प्लॉट और रिग्रेशन प्लॉट प्राप्त होते हैं:

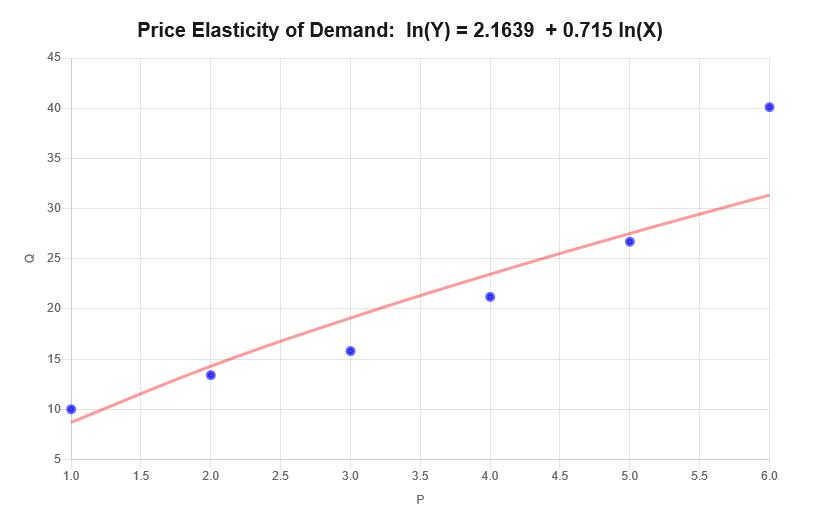
व्याख्या

इस मामले में लोच प्रदान किए गए डेटा के लिए ढलान गुणांक से मेल खाती है, जिसका अर्थ है कि \(\varepsilon = 0.715 \), जिसकी व्याख्या इस प्रकार की जा सकती है:

• कीमत में 1% की वृद्धि होने पर, मांग की मात्रा में औसतन 0.715% की वृद्धि होती है।

अधिक रोचक कैलकुलेटर

नमूना डेटा से मॉडल का अनुमान लगाना सांख्यिकी और अर्थशास्त्र दोनों में आवश्यक एक महत्वपूर्ण क्षमता है। प्रतिगमन मॉडल की गणना करें मॉडल निर्माण के लिए नमूना डेटा का उपयोग करने के सबसे सामान्य अनुप्रयोगों में से एक है।

लेकिन अक्सर ऐसा होता है कि एक नियमित रैखिक मॉडल डेटा को पर्याप्त रूप से फिट नहीं करेगा, जिसके लिए हमें विभिन्न कार्यात्मक संरचनाओं का प्रयास करने की आवश्यकता है। उदाहरण के लिए, हम संभावित रूप से अनुमान लगा सकते हैं लॉग-लॉग रिग्रेशन , ए लघुगणकीय प्रतिगमन या एक बहुपद प्रतिगमन , बस कुछ का उल्लेख करने के लिए, जो नियमित प्रतिगमन की तुलना में आश्रित चर में भिन्नता को समझाने में अधिक सफल हो सकते हैं।

का विकल्प नमूना डेटा से लोच की गणना करना इसका प्रयोग अधिकतर खोजपूर्ण सेटिंग में किया जाता है। लोच की गणना सीधे मांग फ़ंक्शन से की जाती है , जब उपलब्ध हो। अन्य परिस्थितियों में, लोच का अनुमान मूल्य-मांग बिंदुओं की एक जोड़ी से लगाया जाता है। चाप-लोच सूत्र .