लॉग-लॉग मॉडल के बारे में अधिक जानकारी

यह कैलकुलेटर आपको आपके द्वारा प्रदान किए गए डेटा के लिए लॉग-लॉग रिग्रेशन मॉडल की गणना करने की अनुमति देगा। इन डेटा को लॉग-लॉग मॉडल के उपयुक्त प्रतिबिंब की आवश्यकता होती है, जिसमें ln(X) और ln(Y) के बीच संबंध की एक उचित रैखिक डिग्री होनी चाहिए।

एक बार जब आप वैध डेटा प्रदान कर देते हैं, जिसका अर्थ इस मामले में X और Y के लिए सकारात्मक डेटा है, तो आपको आरंभ करने के लिए "गणना करें" बटन पर क्लिक करना होगा ताकि आप प्रक्रिया के सभी चरणों को देख सकें।

लॉग-लॉग मॉडल के मजबूत व्यावहारिक अनुप्रयोग हैं, विशेष रूप से अर्थशास्त्र के क्षेत्र में, जिसमें इसका उपयोग किया जाता है लोच की गणना करें .

लॉग-लॉग मॉडल क्या है?

लॉग-लॉग मॉडल, जैसा कि नाम से ही पता चलता है, एक ऐसा मॉडल है जिसमें \(\ln(X)\), \(\ln(Y)\) के साथ रैखिक जुड़ाव की एक महत्वपूर्ण डिग्री प्रदर्शित करता है। इस तथ्य के आधार पर, यदि उपयुक्त हो प्रतिगमन मॉडल की गणना करें इन परिवर्तन डेटा के लिए, इसलिए हम अनुमान लगाने के लिए प्रतिगमन गुणांक \(a\) और \(b\) की तलाश करते हैं

\[\displaystyle \ln(Y) = a + b \ln(X)\]

तो फिर, लॉग-लॉग मॉडल का कैलकुलेटर रूपांतरित डेटा \(\ln(X)\) और \(\ln(Y)\) के लिए एक नियमित प्रतिगमन मॉडल की गणना तक कम हो जाता है।

लॉग-लॉग मॉडल का अनुमान लगाने के चरण

• स्टेप 1: दिए गए चर X और Y को स्पष्ट रूप से पहचानें। सुनिश्चित करें कि उनका नमूना आकार समान है और वे दोनों सकारात्मक हैं, अन्यथा आप लॉग-लॉग मॉडल नहीं चला सकते
• चरण दो: मूल डेटा X और Y को सहायक ln(X) और ln(x) में बदलें
• चरण 3: एक नियमित प्रतिगमन मॉडल समीकरण का उपयोग करें, जहां आप गणना करते हैं ढलान और Y- अंत आपके लॉग-रूपांतरित डेटा ln(X) और ln(Y) के लिए

एक बार जब आप संबंधित प्रतिगमन गुणांक का अनुमान लगा लेते हैं, तो आप समीकरण \(\displaystyle \ln(Y) = a + b \ln(X)\) लिख सकते हैं, जिसे आप या तो वैसे ही छोड़ सकते हैं, या आप इसे इस प्रकार रूपांतरित कर सकते हैं:

\[\displaystyle Y = e^a \cdot x^b \]

लॉग-लॉग मॉडल व्याख्या

हम गुणांकों की व्याख्या कैसे कर सकते हैं जैसे हमने सीमांत परिवर्तन के दृष्टिकोण से सामान्य प्रतिगमन के साथ किया है? एक विशिष्ट प्रतिगमन समस्या के लिए, आपके पास ढलान गुणांक की व्याख्या Y चर में औसत वृद्धि के रूप में की जा सकती है जब X चर एक इकाई से बढ़ता है।

लॉग-लॉग मॉडल में, यह बिल्कुल उस तरह से काम नहीं करता है, लेकिन इसकी सीमांत व्याख्या समान है। वास्तव में, \(\displaystyle \ln(Y) = a + b \ln(X)\) मॉडल में, हम इसे इस प्रकार से व्याख्या कर सकते हैं:

X में 1% की वृद्धि Y में b% की औसत वृद्धि लाती है स्वाभाविक रूप से, यदि \(b\) है, तो यह कमी से मेल खाता है।

हम इस प्रकार के मॉडल का उपयोग क्यों करते हैं

एक बहुत ही शक्तिशाली कारण यह है कि इसका अर्थशास्त्र में मजबूत अनुप्रयोग है। यह विचार कि मांग की कीमत लोच को लॉग-लॉग मॉडल के ढलान गुणांक की गणना करके आसानी से पाया जाता है, इसे विचार करने के लिए पर्याप्त रूप से प्रासंगिक बनाता है।

इसके अलावा, सापेक्ष सीमांत परिवर्तन के विचार के अर्थशास्त्र में उपयोगिता सिद्धांत में कई अन्य अनुप्रयोग हैं, जो इसे एक अत्यंत व्यावहारिक और लागू मॉडल बनाता है।

लॉग-लॉग प्रतिगमन गणना नमूना

X और Y के लिए निम्नलिखित डेटा पर विचार करें:

एक्स: 1, 2, 3, 4, 5, 6, 7

वाई: 10, 11.1, 13, 15.6, 16.8, 20, 22.4

संगत लॉग-लॉग मॉडल का अनुमान लगाएं और उपयुक्त स्कैटरप्लॉट प्रस्तुत करें

समाधान:

जो गणना का समापन करता है।

अधिक प्रतिगमन कैलकुलेटर

आपको यह आकलन करना होगा कि क्या आपके पास महत्वपूर्ण सहसंबंध गुणांक मॉडल चलाने से पहले ln(X) और ln(Y) के बीच। यह भी एक अच्छा विचार है एक स्कैटरप्लॉट बनाओ डेटा का विश्लेषण यह देखने के लिए किया जाता है कि क्या यह लॉग-लॉग एसोसिएशन से अपेक्षित के अनुरूप है।

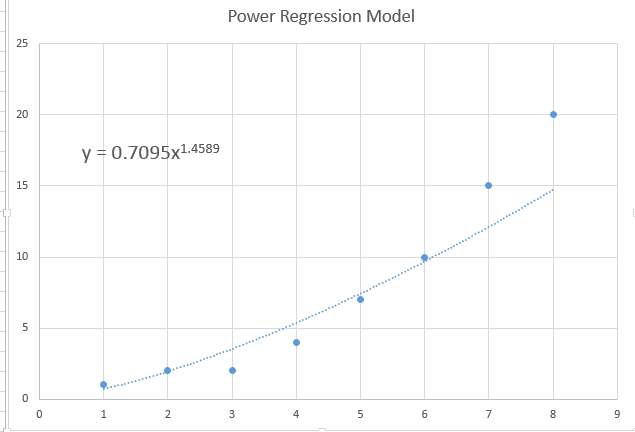
कई बार वक्रता का केवल एक सूक्ष्म स्तर होता है, और डेटा लगभग सपाट पैटर्न दिखाएगा, जो पारंपरिक प्रतिगमन मॉडल के अनुरूप भी है, लेकिन यह एक प्रकार का पैटर्न भी हो सकता है। पावर रिग्रेशन मॉडल बहुत छोटे गुणांक के साथ..