इस असमानता ग्राफर के बारे में

यह कैलकुलेटर आपको सभी चरणों को दिखाते हुए किसी भी सामान्य असमानता का समाधान और ग्राफ ढूंढने में मदद करेगा। आपको दिए गए बॉक्स में टाइप करके एक वेरिएबल (x) की वैध असमानता प्रदान करनी होगी।

उदाहरण के लिए, आप एक साधारण रैखिक असमानता जैसे '3x - 1 < 1/3', या '2x-x^2 <= 3/4' जैसी कोई चीज़ प्रदान कर सकते हैं, जो एक द्विघात असमानता से मेल खाती है।

एक बार जब आप वह असमानता प्रदान कर दें जिसका आप रेखांकन करना चाहते हैं, तो आगे बढ़ें और "हल करें" बटन पर क्लिक करें, ताकि यदि समाधान ढूंढना संभव हो तो सभी चरणों के साथ समाधान प्रस्तुत किया जा सके।

सामान्य समीकरणों को हल करना और व्यवस्थित उपचार के लिए उत्तरदायी संरचनाओं के एक विशिष्ट सेट को छोड़कर, सामान्य असमानताएं आम तौर पर एक कठिन कार्य है।

कुछ ऐसे प्रकार हैं जो सटीक समाधान की अनुमति देते हैं रैखिक असमानताएँ और बहुपद असमानताएँ ।

असमानता का एक महत्वपूर्ण प्रकार जिसे आप हल करना चाहेंगे वह तर्कसंगत असमानताओं का मामला है, जिसमें आप बहुपदों के भागफल की पहचान कर सकते हैं। वे असमानताएँ दिलचस्प हैं क्योंकि उनमें शून्य से संभावित विभाजन हैं जिन्हें संबोधित करने की आवश्यकता है। तर्कसंगत असमानता के विचार को सामान्य रूप से कार्यों के भागफल तक आसानी से बढ़ाया जा सकता है, जरूरी नहीं कि बहुपद तक

असमानता का रेखांकन कैसे करें

इसका सबसे सरल उत्तर यह है: किसी असमानता का रेखांकन करने के लिए, आपको यह जानना होगा कि इसे कैसे हल किया जाए। किसी असमानता का आलेखीय समाधान आमतौर पर x अक्ष पर एक अंतराल या कई जुड़े हुए अंतरालों के रूप में दर्शाया जाता है।

तो, जैसा कहा जा रहा है, किसी असमानता का रेखांकन पहले उसे हल करने से शुरू होगा, जिसमें वास्तविक रेखा में मूल्यों का एक सेट ढूंढना शामिल है जो प्रदान की गई असमानता को संतुष्ट करता है।

आप संभावित रूप से ग्राफ़ को एक स्टैंडअलोन अंतराल के रूप में प्रस्तुत कर सकते हैं, या आप असमानता के अंतर्निहित अभिव्यक्ति के ग्राफ़ के साथ असमानता समाधानों को प्लॉट कर सकते हैं: आइए इसे याद रखें असमानताओं को हल करें , आप सभी पदों को एक तरफ भेज देते हैं (जो आपको अंतर्निहित अभिव्यक्ति देता है) और एक सहायक समीकरण को हल करते हैं

असमानताओं को हल करने और रेखांकन करने के चरण

• Letsunt 1: सभी पदों को एक तरफ से गुजारें, ताकि आपके पास एक तरफ एक अभिव्यक्ति हो, और दूसरी तरफ शून्य हो
• Their दो दो: असमानता से (जब एक तरफ सब कुछ हो और दूसरी तरफ शून्य), एक सहायक समीकरण बनाएं
• Theirण 3: इस समीकरण को ऐसी विधि से हल करें जो इसकी संरचना के लिए उपयुक्त हो (विभिन्न प्रकार के समीकरणों के लिए विशिष्ट तकनीकों और दृष्टिकोण की आवश्यकता होगी)
• च ४: ४: सहायक समीकरणों के वास्तविक समाधानों (जटिल समाधानों के विपरीत वास्तविक) के आधार पर, आप अपने महत्वपूर्ण बिंदु बनाते हैं, और उन्हें आरोही क्रम में क्रमबद्ध करते हैं
• च ५: ५: आपको उन बिंदुओं को भी देखना होगा जहां अभिव्यक्ति अपरिभाषित है। इसका एक उल्लेखनीय मामला तर्कसंगत असमानताओं के साथ होता है, जिसमें आपके पास एक हर है जो एक बहुपद है, इसलिए तब अभिव्यक्ति हर के शून्य पर अपरिभाषित होगी। तो आप हर के शून्य को महत्वपूर्ण बिंदुओं की सूची में जोड़ें
• च viry: 6: अपने महत्वपूर्ण बिंदुओं के साथ, आप लगातार महत्वपूर्ण बिंदुओं का उपयोग करके अंतराल का निर्माण करते हैं (प्रारंभिक और अंतिम महत्वपूर्ण बिंदुओं के रूप में -∞ और ∞ का उपयोग करके)
• Their च 7: प्रत्येक अंतराल के लिए, अभिव्यक्ति के चिह्न का विश्लेषण करें और देखें कि क्या यह असमानता के चिह्न के साथ संगत है। यदि ऐसा है, तो अंतराल असमानता के समग्र समाधान का एक हिस्सा होगा

विश्लेषण के लिए महत्वपूर्ण बिंदुओं का उपयोग करना अत्यंत महत्वपूर्ण है, क्योंकि इस तरह से आप सुनिश्चित होते हैं कि अभिव्यक्ति प्रत्येक अंतराल के भीतर संकेत नहीं बदलती है, ताकि समस्या यह आकलन करने में कम हो जाए कि क्या उन महत्वपूर्ण अंतरालों में से प्रत्येक के लिए असमानता हल हो गई है।

इसे थोड़ा अधिक मूर्त बनाने के लिए, आपके पास कुछ असमानता दी गई है, और फिर आपने सब कुछ एक तरफ कर दिया है, इसलिए आपके पास \(f(x) \le 0\) के रूप में कुछ है। उदाहरण के लिए, यह \(x^2 - x + 1 \le 0\) जैसा कुछ हो सकता है।

तो फिर आप \(f(x) \le 0\) लेते हैं और आपको सहायक समीकरण \(f(x) = 0\) मिलता है। आप व्यंजक \(f(x)\) लेते हैं और पाते हैं कि इसके शून्य महत्वपूर्ण बिंदु हैं। लेकिन आप न केवल ऐसा करते हैं, बल्कि यह भी देखते हैं कि क्या \(f(x)\) कहीं भी अपरिभाषित है (शून्य से विभाजन, आदि)। इसे हर जगह परिभाषित किया जा सकता है, जैसे \(x^2 - x + 1\) मामले में, लेकिन यदि आपको ऐसे बिंदु मिलते हैं जहां अभिव्यक्ति अपरिभाषित है, तो आप इसे महत्वपूर्ण बिंदुओं की सूची में जोड़ देते हैं।

फिर आप लगातार महत्वपूर्ण बिंदुओं के आधार पर अंतराल का निर्माण करते हैं। \(f(x) \le 0\) के लिए, आप समाधान के एक भाग के रूप में उन अंतरालों को लेंगे जहां अभिव्यक्ति का मान नकारात्मक है। यदि मूल असमानता \(f(x) \ge 0\) होती तो आप समाधान के एक भाग के रूप में उन अंतरालों को लेंगे जहां अभिव्यक्ति का मान सकारात्मक है

यह असमानता ग्राफर कैसे काम करता है

हमारा ऑनलाइन असमानता ग्राफर बुनियादी बीजगणित में सबसे बोझिल प्रक्रियाओं में से एक का ध्यान रखेगा, जो असमानता के समाधान खोजने और उन्हें रेखांकन करने से संबंधित है। हमारे कैलकुलेटर का एक बड़ा फायदा यह है कि यह संभव होने पर सभी चरण दिखाएगा।

सबसे पहले, ग्राफर एक उपयुक्त सहायक समीकरण को हल करके असमानता को हल करेगा। इस प्रक्रिया में विशिष्ट ज्ञात संरचनाओं का पता लगाने की आवश्यकता होती है, क्योंकि सभी संरचनाओं के लिए अलग-अलग दृष्टिकोण की आवश्यकता होती है। उदाहरण के लिए, एक तर्कसंगत असमानता को हल करने के लिए (जिसमें दो बहुपदों का भागफल शामिल होता है) जैसे कि उदाहरण के लिए

\[\displaystyle \frac{x^2-2x}{x-1} \ge 4 \]

उदाहरण के लिए, आपको \(x^2 + 3x < 1\) जैसी द्विघात असमानता को हल करने के लिए उपयोग किए जाने वाले दृष्टिकोण से भिन्न दृष्टिकोण की आवश्यकता होगी, और यह कैलकुलेटर उन सभी विवरणों को लेगा।

यदि कोई पारंपरिक या आमतौर पर ज्ञात संरचना का पता नहीं चलता है, तो आमतौर पर उपयोग किए जाने वाले विभिन्न प्रतिस्थापनों का उपयोग किया जाएगा, जैसे उदाहरण के लिए \(u = \sqrt x\) या \(u = \sin x\)। यदि कुछ भी काम नहीं करता है, तो कैलकुलेटर निरीक्षण और संख्यात्मक रूप से समाधान खोजने का प्रयास करेगा, ताकि कम से कम समाधानों का अंदाजा मिल सके।

आप असमानता का ग्राफ कैसे प्रस्तुत करते हैं?

जैसा कि हमने ऊपर उल्लेख किया है, यह वास्तव में पत्थर पर नहीं लिखा गया है, लेकिन सबसे आम तरीका असमानता की अंतर्निहित अभिव्यक्ति को रेखांकन करना है, और असमानता को संतुष्ट करने वाले x मानों को उजागर करना है। यह संभवतः इसके लिए सबसे अच्छा ग्राफ़िंग प्रारूप है, और इसका उपयोग इस ग्राफर द्वारा किया जाता है।

आप एक स्टैंडअलोन अंतराल ऑब्जेक्ट भी बना सकते हैं, लेकिन यह संभवतः कम बताने वाला है, क्योंकि यह असमानता के साथ वास्तव में क्या हो रहा है, इसका परिप्रेक्ष्य खो देता है।

उदाहरण: असमानताओं का रेखांकन

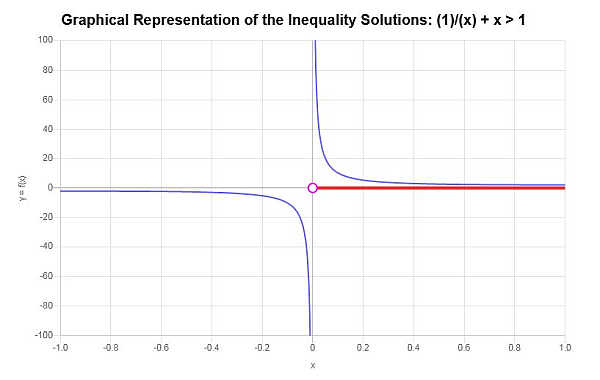
निम्नलिखित असमानता का ग्राफ़ बनाएं: \(\frac{1}{x}+x > 1\)

तमाम: हमें निम्नलिखित असमानताएँ दी गई हैं जिन्हें हल करने की आवश्यकता है:

\[\frac{1}{x}+x > 1\]

हमें असमानता की सभी शर्तों को एक तरफ रखना होगा:

\[x+\frac{1}{x}-1>0\]

सहायक समीकरण हल करना

उपरोक्त असमानता से, हमें संबंधित समीकरण प्राप्त होता है जिसे पहले हल करने की आवश्यकता है:

\[x+\frac{1}{x}-1=0\]

महत्वपूर्ण बिंदुओं का विश्लेषण

हमें पाए गए महत्वपूर्ण बिंदुओं को (अंश और हर की वास्तविक जड़ों से) आरोही क्रम में व्यवस्थित करने की आवश्यकता है, सभी लगातार महत्वपूर्ण बिंदुओं के साथ अंतराल को परिभाषित करें, और उनमें से प्रत्येक अंतराल पर असमानता के बाएं हाथ के आकार के संकेत का आकलन करें। .

एकमात्र महत्वपूर्ण बिंदु जो पाया गया वह \(0\) है।

इसके आधार पर, हमें निम्नलिखित अंतरालों का विश्लेषण करने की आवश्यकता है:

• अंतराल \(\left(-\infty, 0\right)\) के लिए: अंश धनात्मक है और हर ऋणात्मक है, इसलिए बाईं ओर ऋणात्मक है, जिसका अर्थ है कि \(\left(-\infty, 0\right)\) समाधान का हिस्सा नहीं है।

• अंतराल \(\left(0, \infty\right)\) के लिए: अंश धनात्मक है और हर धनात्मक है, इसलिए बाईं ओर धनात्मक है, इसलिए \(\left(0, \infty\right)\) समाधान का हिस्सा है।

असमानता का समाधान

प्रदान की गई असमानता के आधार पर, और महत्वपूर्ण बिंदुओं का विश्लेषण करते हुए, हम पाते हैं कि असमानता का समाधान है: \(x > 0\)।

अंतराल संकेतन का उपयोग करते हुए, समाधान इस प्रकार लिखा गया है:

\[\left(0,\infty\right)\]

असमानता ग्राफर से निम्नलिखित प्राप्त होता है:

जो गणना का समापन करता है।

उदाहरण: बहुपद असमानताओं का रेखांकन

असमानता का ग्राफ खोजें: \(x^2 - 2x \ge 4\)

समाधान:

हमें असमानता की सभी शर्तों को एक तरफ रखना होगा:

\[x^2-2x-4\ge0\]

सहायक समीकरण हल करना

उपरोक्त असमानता से, हमें संबंधित समीकरण प्राप्त होता है जिसे पहले हल करने की आवश्यकता है:

\[x^2-2x-4=0\]

द्विघात सूत्र का उपयोग करना

फार्म \(a x^2 + bx + c = 0\)के एक द्विघात समीकरण के लिए, जड़ों को निम्न सूत्र का उपयोग करके गणना की जाती है:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]

इस मामले में, हमारे पास है कि हमें जिस समीकरण को हल करने की आवश्यकता है वह \(\displaystyle x^2-2x-4 = 0\)है, जिसका अर्थ है कि संबंधित गुणांक हैं:

\[a = 1\] \[b = -2\] \[c = -4\]

सबसे पहले, हम जड़ों की प्रकृति का आकलन करने के लिए भेदभाव की गणना करेंगे।भेदभाव की गणना की जाती है:

\[\Delta = b^2 - 4ac = \displaystyle \left( -2\right)^2 - 4 \cdot \left(1\right)\cdot \left(-4\right) = 20\]

चूंकि इस मामले में हमें भेदभावपूर्ण \(\Delta = \displaystyle 20 > 0\)है, जो सकारात्मक है, हम जानते हैं कि समीकरण में दो अलग -अलग वास्तविक जड़ें हैं।

अब, इन मूल्यों को जड़ों के लिए सूत्र में प्लग करना:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{2 \pm \sqrt{\left(-2\right)^2-4\left(1\right)\left(-4\right)}}{2\cdot 1} = \displaystyle \frac{2 \pm \sqrt{20}}{2}\]

तो फिर, हम पाते हैं कि:

\[ {x}_1 = \frac{2}{2}-\frac{1}{2}\sqrt{20}=\frac{2}{2}-\sqrt{5}=1-\sqrt{5}=-\sqrt{5}+1 \] \[{x}_2 = \frac{2}{2}+\frac{1}{2}\sqrt{20}=\frac{2}{2}+\sqrt{5}=1+\sqrt{5}=\sqrt{5}+1\]

इस मामले में, द्विघात समीकरण \( \displaystyle x^2-2x-4 = 0 \), की दो वास्तविक जड़ें हैं, इसलिए फिर:

\[\displaystyle x^2-2x-4 = \left(x+\sqrt{5}-1\right)\left(x-\sqrt{5}-1\right)\]

तो फिर मूल बहुपद \(\displaystyle p(x) = x^2-2x-4 = \left(x+\sqrt{5}-1\right)\left(x-\sqrt{5}-1\right) \)के रूप में फैक्टर किया जाता है, जो कारक को पूरा करता है।

महत्वपूर्ण बिंदुओं का विश्लेषण

आरोही क्रम में व्यवस्थित पाए गए महत्वपूर्ण बिंदुओं की सूची है: \(-\sqrt{5}+1\), \(\sqrt{5}+1\)।

इसके आधार पर, हमें निम्नलिखित अंतरालों का विश्लेषण करने की आवश्यकता है:

• अंतराल \(\left(-\infty, -\sqrt{5}+1\right)\) के लिए: बाईं ओर सकारात्मक है, तो फिर \(\left(-\infty, -\sqrt{5}+1\right)\) समाधान का हिस्सा है।

• अंतराल \(\left(-\sqrt{5}+1, \sqrt{5}+1\right)\) के लिए: बाईं ओर नकारात्मक है, इसलिए \(\left(-\sqrt{5}+1, \sqrt{5}+1\right)\) समाधान का हिस्सा नहीं है।

• अंतराल \(\left(\sqrt{5}+1, \infty\right)\) के लिए: बाईं ओर सकारात्मक है, जिसका अर्थ है कि \(\left(\sqrt{5}+1, \infty\right)\) समाधान का हिस्सा है।

असमानता का समाधान

प्रदान की गई असमानता के आधार पर, और महत्वपूर्ण बिंदुओं का विश्लेषण करते हुए, हम पाते हैं कि असमानता का समाधान है: \(x \le -\sqrt{5}+1\) या \(x \ge \sqrt{5}+1\)।

अंतराल संकेतन का उपयोग करते हुए, समाधान इस प्रकार लिखा गया है:

\[\left(-\infty,-\sqrt{5}+1\right] \cup \left[\sqrt{5}+1,\infty\right)\]

रेखांकन:

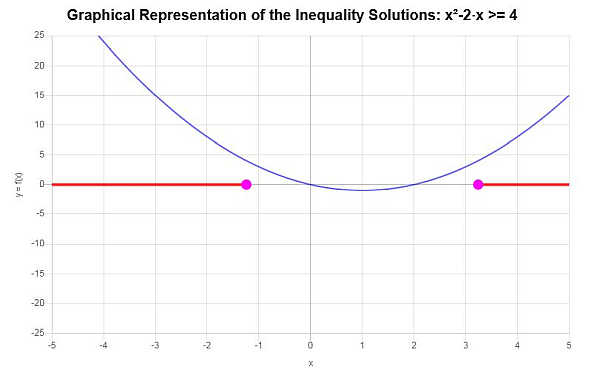
जो गणना का समापन करता है।

अधिक बीजगणित कैलकुलेटर

जैसे-जैसे आप बीजगणित और कैलकुलस सीखने में आगे बढ़ते हैं, आपको संभवतः धीरे-धीरे इसका एहसास हो गया होगा समीकरण हल करना एक महत्वपूर्ण भूमिका निभाएं. और जैसे-जैसे आप और अधिक सीखते हैं, आपको एहसास होता है कि कभी-कभी हमारे पास कम जानकारी होती है और हमें समस्या का सामना करना पड़ता है असमानताओं का समाधान ।

संक्षेप में, असमानताओं को हल करना समीकरणों को हल करने से अधिक कठिन नहीं है, इसके लिए बस कुछ और संगठित कदम उठाने पड़ते हैं। मुख्य समस्या यह है कि हम अधिकांश समीकरणों को कम से कम सटीक रूप से हल नहीं कर सकते हैं।

और समीकरणों को संख्यात्मक रूप से हल करने पर भी, हमारे पास अभी तक यह सुनिश्चित करने के अच्छे तरीके नहीं हैं कि हमने सभी संभावित समीकरणों के सभी समाधान ढूंढ लिए हैं। कुछ उल्लेखनीय समीकरण जिन्हें हल किया जा सकता है और हर समय अनुप्रयोगों में दिखाई दे सकते हैं बहुपद rayrण , जिसे आप अधिकतर मानक तरीकों का उपयोग करके हल कर सकते हैं (लेकिन केवल निम्न डिग्री वाले बहुपदों के लिए)

सबसे अधिक पूछे जाने वाले प्रकार की असमानताओं में से एक जिसे आपको अपने गणित परीक्षणों में हल करने की आवश्यकता है, तर्कसंगत असमानताएं हैं, क्योंकि वे सबसे कठिन सरल असमानताएं हैं जिनका आप समाधान खोजने की गारंटी दे सकते हैं (बशर्ते कि इसमें शामिल डिग्री काफी कम हो, या बहुपद काफी सरल हैं)।