حول حاسبة مرونة القوس

استخدم هذه الآلة الحاسبة لتقدير مرونة السعر عندما يكون لديك معلومات عن السعر والطلب عند نقطتين. هذا بالنسبة لـ \(P_1\) معين, لديك كمية معينة مطلوبة \(Q_1\), ثم عندما يتغير السعر إلى \(P_2\), تتفاعل الكمية المطلوبة بالتغير إلى \(Q_2\).

يتعين عليك تقديم قيم رقمية صالحة للأسعار والكميات المطلوبة المرتبطة بها. بمجرد كتابة هذه المعلومات في المربعات المقابلة, انقر فوق الزر الذي يقول "احسب" لمشاهدة جميع خطوات عملية الحساب.

في نظرية الاقتصاد يزعم المرء أن السلعة العادية ستشهد انخفاضًا في الكمية المطلوبة كاستجابة لارتفاع الأسعار.

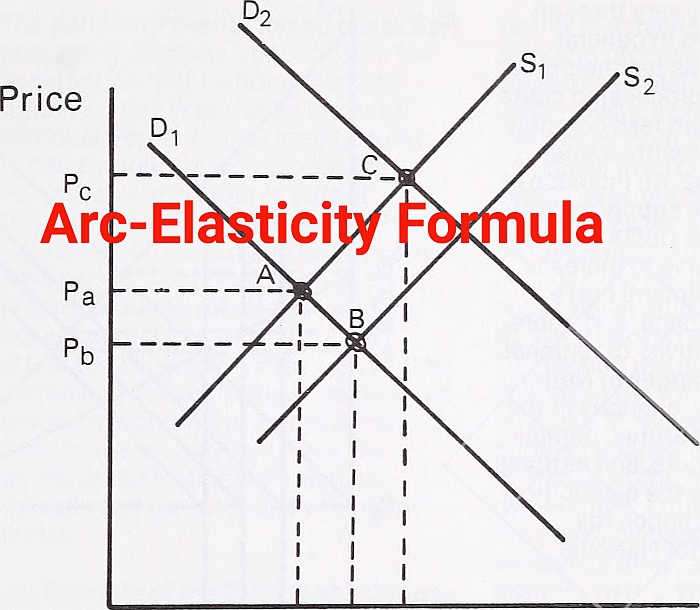
ما تحتاج إلى فهمه حول مرونة الطلب القوسية

في علم الاقتصاد, المرونة هي مقياس رقمي لاستجابة الطلب للتغيرات في السعر. إذا ارتفع السعر بمقدار معين, فسوف نلاحظ رد فعل في الكمية المطلوبة, والنسبة المئوية النسبية للتغير في الكمية المطلوبة مقابل النسبة المئوية النسبية للتغير في السعر هي ما نسميه مرونة الطلب السعرية.

من الناحية الرياضية, يمكن التعبير عن ذلك بالصيغة التالية:

\[ \text{Elasticity} = \displaystyle \frac{\%\Delta Q}{\%\Delta P}\]

نحن بحاجة إلى معرفة أن المرونة هي نقطة, لذا عند أخذ تغير صغير ولكنه محدود في السعر, والذي يُشار إليه بـ \(\Delta P\), فإننا نقرب فقط قيمة المرونة النقطية الحقيقية

استخدام تغييرات الأسعار اللامتناهية في الصغر

إن التجريد الأفضل لهذا سيكون باستخدام صغير بشكل لا نهائي تغير السعر, وفي هذه الحالة سنحصل على تعبير دقيق للمرونة باستخدام المشتقات , والتي سيتم كتابتها على النحو التالي

\[ \text{Elasticity} = \displaystyle \frac{dQ}{dP}\frac{P}{Q}\]

في سياق الصيغة أعلاه, \(\frac{dQ}{Q}\) هي النسبة المئوية للتغير الضئيل في الكمية المطلوبة مقارنة بالنسبة المئوية للتغير الضئيل في السعر, والتي هي \(\frac{dP}{P}\)

صيغة مرونة القوس

في كثير من الأحيان, لا نملك القدرة على الوصول إلى دالة الطلب الفعلية التي قد تكون ضرورية لأغراض التمايز, ولا نملك سوى بيانات منفصلة. إحدى الطرق لإجراء تقريب أفضل للمرونة هي استخدام الصيغة التالية:

\[ \varepsilon_{ARC} = \displaystyle \frac{Q_2 - Q_1}{P_2 - P_1}\frac{P_1 + P_2}{Q_1 + Q_2}\]

وهو تبسيط لـ

\[ \varepsilon_{ARC} = \displaystyle \frac{Q_2 - Q1}{P_2 - P_1}\frac{(P_1 + P_2)/}{(Q_1 + Q_2)/2}\]

ويشير هذا إلى أننا نستخدم متوسط النقاط المقابلة لتقدير النسب المئوية للتغيرات في السعر والكمية المطلوبة.

خطوات استخدام صيغة مرونة القوس

• الخطوة 1: حدد نقاط السعر P1 وP2, وحدد الكميات المطلوبة المقابلة مثل Q1 وQ2, مع إجراء الارتباط الصحيح بين السعر الذي يتوافق مع الكمية المطلوبة
• الخطوة 2: بمجرد حصولك على P1 وP2 وQ1 وQ2, استخدم الصيغة e = (Q2 - Q1)/(P2 - P1)*(P1 + P2)/(Q1 + Q2)
• الخطوه 3: ثم تفسر المرونة e باعتبارها النسبة المئوية للتغير في الكمية المطلوبة نتيجة لتغير بنسبة 1% في السعر

لاحظ أنه في أغلب الأحيان, وفي أغلب الأحيان, تكون المرونة سالبة, لأن الزيادة في السعر تؤدي في أغلب الأحيان إلى انخفاض الكمية المطلوبة. ومن الجيد الإبلاغ عن المرونة كرقم سلبي, ولكن انتبه إلى أنه في بعض الأحيان يتم الإبلاغ عنها من حيث قيمتها المطلقة.

التطبيقات العملية لمرونة الطلب القوسية

تلعب مرونة الطلب دورًا رئيسيًا في الاقتصاد الجزئي, حيث إنها تعطي صورة لمشاعر العملاء من حيث حساسيتهم لتغيرات الأسعار. عندما تعمل الشركات في قطاع من قيم المرونة المنخفضة (بين -1 و 0), وهو ما يسمى بالنطاق غير المرن, فهناك مجال لزيادات الأسعار ومع ذلك تحصل على انخفاض معتدل نسبيًا في الطلب على الكمية, مما يؤدي إلى زيادة صافية في الإيرادات.

من ناحية أخرى, عندما تعمل الشركات في قطاع من قيم المرونة العالية (أقل من -1), وهو ما يسمى بالنطاق المرن, فإن زيادات الأسعار تؤدي إلى انخفاضات كبيرة نسبيا في الطلب على الكمية, مما يؤدي إلى انخفاض صاف في الإيرادات.

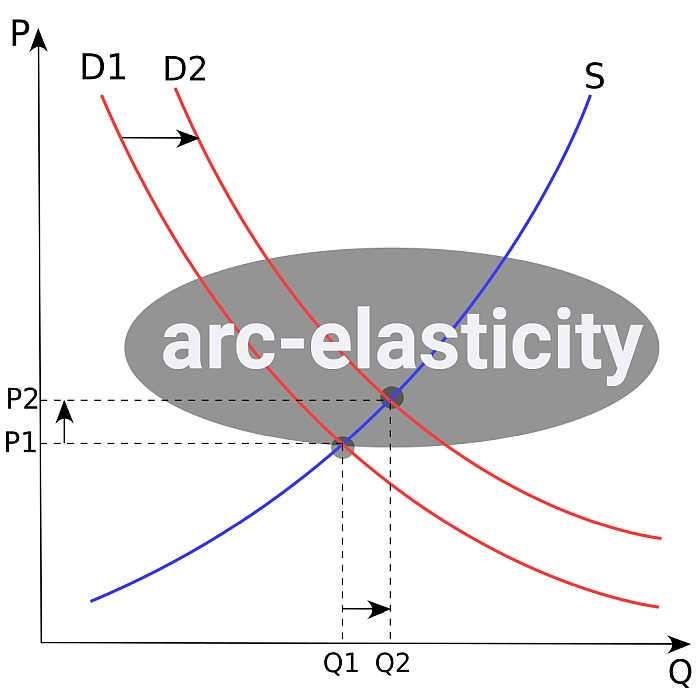
مثال لتقدير صيغة مرونة القوس

تعتبر سلعة معينة سلعة عادية, وتنخفض الكمية المطلوبة منها عندما يرتفع السعر. في البداية, عند سعر 25 دولارًا, كانت الكمية المطلوبة 200 وحدة, وعندما ارتفع السعر إلى 28 دولارًا, انخفضت الكمية المطلوبة إلى 170 وحدة. قم بتقدير مرونة الطلب السعرية بناءً على هذه المعلومات.

حل: نحن بحاجة إلى حساب مرونة القوس بناءً على المعلومات التالية المقدمة لنقطتي سعر والكميات المطلوبة المقابلة لهما

Price 1 \((P_1)\) =	$\(25\)
Price 2 \((P_2)\) =	$\(28\)
Quantity Demanded 1 \((Q_1)\) =	\(200\)
Quantity Demanded 2 \((Q_2)\) =	\(170\)

في هذه الحالة, يجب استخدام صيغة مرونة القوس. الصيغة هي:

\[ \varepsilon_{ARC} = \displaystyle \left(\frac{Q_2 - Q1}{P2_P1}\right)\left(\frac{P_1 + P_2}{Q_1 + Q_2}\right)\]

لكي نتمكن من إجراء الحساب, نحتاج فقط إلى إدخال القيم المقابلة:

\[ \begin{array}{ccl} \varepsilon_{ARC} & = & \displaystyle \left(\frac{Q_2 - Q_1}{P_2 - P_1} \right)\left(\frac{P_1 + P_2}{Q_1 + Q_2}\right) \\\\ \\\\ & = & \displaystyle \displaystyle \left( \frac{170 - 200}{28 - 25} \right) \left( \frac{25 + 28}{200 + 170} \right) \\\\ \\\\ & = & -1.432 \end{array}\]

مرونة القوس في هذه الحالة هي \(\varepsilon = -1.432 \), والتي يمكن تفسيرها على النحو التالي:

• مقابل زيادة قدرها 1% في السعر, يوجد انخفاض متوسط قدره 1.432% في الكمية المطلوبة, ضمن النطاق السعري 25 دولارًا و28 دولارًا.

حاسبات المرونة الأخرى

قد يتخذ حساب مرونة الطلب السعرية أشكالاً مختلفة. أحد هذه الأشكال هو ما نقوم به في هذه الآلة الحاسبة, والذي يتضمن استخدام صيغة المرونة القوسية عندما تكون نقطتا السعر والكمية المطلوبة متاحتين

يمكننا أن نأخذ هذا إلى أبعد من ذلك مع هذا حاسبة جدول مرونة القوس , حيث تقدم جدولاً للسعر والكمية المطلوبة, ويتم حساب المرونة نقطة بنقطة عن طريق التقريب باستخدام مرونة القوس.

في بعض الحالات المحددة, قد ترغب في افتراض مرونة ثابتة, واستخدام هذه المرونة من حاسبة بيانات العينة, والتي ستؤدي إلى نتائج مفيدة فقط إذا اتبعت بيانات السعر والطلب نموذجًا مناسبًا نمط السجل-السجل .

الفكرة هنا هي أن لدينا دالة طلب فعلية, حيث ببساطة حساب المرونة من دالة الطلب , الحصول على تقدير دقيق لكل نقطة من نقاط المرونة, على عكس حالة مرونة القوس والتي تكون عبارة عن قيمة تقريبية.