一对一功能

本计算器将帮助您评估函数是否一一对应,并显示所有步骤。首先,您需要提供函数。这个函数可以是简单的线性或二次函数,如 "y = x^2 - 1",或者您也可以选择 有理函数 如 "f(x) = (x-1)/(x+3)"。

然后,如果您对所提供的信息感到满意,并确定函数有效,就可以点击 "计算 "按钮,向您显示计算过程的所有步骤。

一一对应函数的概念在代数和微积分中非常重要。有许多简单的方法来检验一一对应关系,其中之一就是 水平线测试 但由于其性质,它更容易用来反证函数是一一对应的。要证明一个函数是一一对应的,我们需要一个 方程求解 分析过程。

什么是一对一流程

简单地说,一一对应或注入函数是指对于两个不同的 \(x_1\) 和 \(x_2\) 来说,它们通过 \(f(x)\) 的图像值是不同的,这在数学上意味着

\[\displaystyle x_1 \ne x_2 \Rightarrow f(x_1) \ne f(x_2) \]

有些教师喜欢用稍有不同的写法,但仍然是等价的：函数是一一对应的,如果

\[\displaystyle f(x_1) = f(x_2) \Rightarrow x_1 = x_2 \]

这就是说,如果函数的图形与相同的值（水平线）相交,那么只有当点相同时才会发生这种情况。所以,你的意思是说,没有两个不同的点与水平线相交。所以,你只是在重申 水平线测试 .

如何检查函数是否一一对应？

• 步骤1： 从原始函数 f(x) 开始,设置方程 y = f(x)
• 第2步： 尝试求解 x
• 第3步： 如果找到一个以上的解,则函数不是一一对应的；如果只有一个解或无解,则函数是一一对应的。

通常,您会进行一些基本检查,以确保该函数显然不是一一对应的,这可能是因为您可以很容易地找到一条水平线来使 HLT 失效。

然后,您将寻找一些基本的视觉特性：函数是否总是递增的（那么它就是一一对应的）,函数总是递减的情况也是如此。

一一对应与求逆有什么关系？

简单地说,要找到一个函数的逆,这个函数必须是一一对应的,至少在某个子域上是如此。很多时候,我们会对域进行限制,使函数在受限域内是一一对应的,否则就不是一一对应了。

例如,\(f(x) = x^2\) 整体上不是一一对应的。为什么呢,因为你可以取两个不同的点 \(x_1 = -1\) 和 \(x_2 = 1\),然后发现 \(f(x_1) = (-1)^2 = 1\) 和 \(f(1) = 1^2 = 1\),这意味着该性质（一一对应的特性）

\[\displaystyle x_1 \ne x_2 \Rightarrow f(x_1) \ne f(x_2) \]

不满足。现在,如果我们不考虑整条实线 \(\R\),而只考虑正值,我们就可以得出结论：函数在正实值上是一一对应的（提示：在该子域上,函数是递增的）

是否有公式可以评估函数是否一一对应？

可惜不是。我的意思是,我们可以把 \(\displaystyle x_1 \ne x_2 \Rightarrow f(x_1) \ne f(x_2) \) 视为一对一公式,但这与其说是一个公式,不如说是一个逻辑条件。

不过,有一种非常宽泛的通用程序可以用来测试函数是否一一对应,这就是上文所解释的。没有 "一一对应公式"。如果非要找一个,那就是 y = f(x)。

我们只需求解 x,仅此而已。归根结底,这取决于 f(x) 到底是什么。一个非常复杂,迂回曲折的函数可能会给求解带来很多困难,也许你需要一个函数计算器来解决,甚至使用函数计算器也可能会失败。

你可能会想,这是为什么呢？究其根本,是因为我们没有解所有方程的技术。我们只是在某些特定类型的方程上做了一些力所能及的事情,但还远远没有掌握解所有方程的精确方法。

示例：一对一功能一对一功能

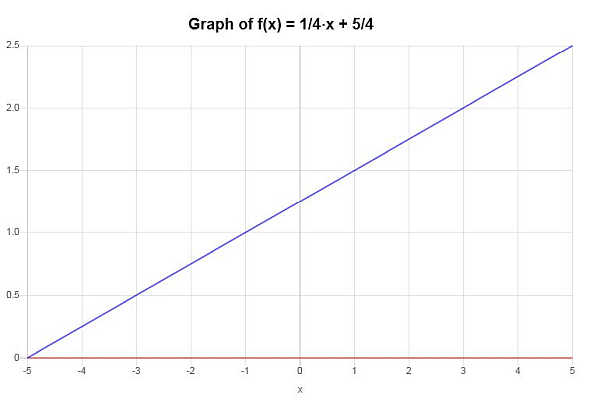
下面的函数是否具有注入性？\(f(x) = \frac{1}{4} x + \frac{5}{4}\)

解决方案：

我们获得了以下功能：

\[f(x) = \frac{1}{4} x + \frac{5}{4}\]

然后,为了评估给定函数是否一一对应,我们需要求解 \(x\),并确定是无解,一解还是多解。起始方程为

\[y=\frac{1}{4}x+\frac{5}{4}\]

将 \(x\) 放在左侧,将 \(y\) 和常数放在右侧,我们得到

\[\displaystyle -\frac{1}{4}x = -y -\left(-\frac{5}{4}\right)\]

现在,用方程两边除以 \(-\frac{1}{4}\),求解 \(x\),得到如下结果

\[\displaystyle x=-\frac{1}{-\frac{1}{4}}y+\frac{\frac{5}{4}}{-\frac{1}{4}}\]

并简化我们最终得到以下

\[\displaystyle x=4y-5\]

因此,对给定的线性方程求解 \(x\) 得到 \(x=4y-5\),它只有一个实数解,所以给定的函数是一一对应的。

总结

根据上一节的结论,可以得出给定函数是一一对应的。

在图形上。

示例：1 对 1 功能

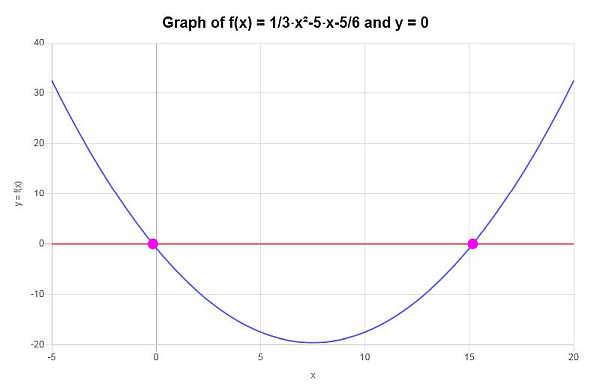
证明或反证下列函数是一一对应的：\(f(x) = \frac{1}{3} x^2 - 5x - \frac{5}{6}\)

解决方案： 为了评估给定函数是否一一对应,我们需要求解 \(x\),并确定是无解,一解还是多解。我们需要使用的起始方程是

\[y=\frac{1}{3}x^2-5x-\frac{5}{6}\]

最初的步骤。 在这种情况下,我们首先需要对给定方程进行化简,为此,我们要执行以下化简步骤：

那么,解决办法是

\[x_1=-\frac{1}{2}\sqrt{12y+235}+\frac{15}{2} \] \[x_2=\frac{1}{2}\sqrt{12y+235}+\frac{15}{2} \]

一对一状态

根据上述工作,可以得出结论：给定函数不是一对一函数,因为它没有通过水平线测试,例如,直线 \(y = 0\) 是一条与给定函数交叉不止一次的水平线。

具体情况如下：

更多有趣的代数计算器

一对一函数的概念通常被认为是理所当然的,但我要说,它是一个非常重要,至关重要的概念。这是因为一对一的概念与单调函数（递增或递减函数）的概念密切相关,同样也与 "一对一 "的概念密切相关。 反函数计算 及其图形。

然而,由于大多数重要的代数和微积分概念之间都有着紧密的联系,因此很多时候很难做到 "只见树木,不见森林"。 功能分析 这是你经常要做的事情之一,因此掌握这方面的技能是一件好事。