Подробнее об этом генераторе квадратичных графов

Этот калькулятор квадратичных графиков позволит вам построить график для любой квадратичной функции, которую вы предоставите. Это может быть любая действительная квадратичная функция, например, x^2 - 3x + 1/2, но вы также можете предоставить квадратичную функцию, которая не упрощается, например, x^2 - 3x - 4 - 1/2 x^2 - 1/5, при условии, что это действительная квадратичная функция.

Как только вы введете правильное квадратичное выражение, вы можете нажать на кнопку "Вычислить", и на экране появится окно график функции будет сгенерирован, показывая этапы вычисления вершина параболы и Ось симметрии а также .

Квадратичные функции занимают главенствующее место в базовой алгебре, поскольку они часто используются в контексте решения задачи квадратные уравнения и прикладные проблемы. По сути, они являются базовыми полиномы , которые обладают множеством интересных свойств.

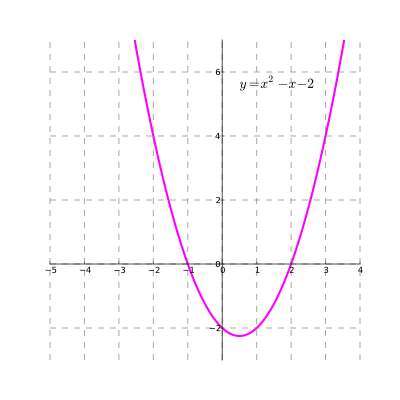
Как построить график квадратичной формы?

Построить график квадратичной функции просто, в том смысле, что вы знаете, что ВСЕ квадратичные функции будут иметь форму параболы. Но все же парабол бесконечно много. Нам нужно знать немного больше, чтобы определить точную параболу, которая представляет данную квадратичную функцию.

Шаги для нахождения графика квадратичной функции

• Шаг 1: Четко определите заданную квадратичную функцию и при необходимости упростите ее
• Шаг 2: После упрощения определите функцию в виде f(x) = ax² + bx + c. Обратите внимание, что a не может быть нулем
• Шаг 3: Если a > 0, вы знаете, что график будет параболой, раскрывающейся вверх, тогда как если a < 0, вы знаете, что график будет параболой, раскрывающейся вниз
• Шаг 4: Ось симметрии находится в точке x* = -b/(2a), что указывает на "центр" параболы
• Шаг 5: Обратите внимание, что x* = -b/(2a) - координата x вершины параболы, а y* = f(x*) = a(x*)² + b(x*) + c - координата y вершины

Этого должно быть достаточно, чтобы иметь четкое представление о соответствующем квадратичном графике. Дальнейшим шагом будет построение некоторых точек на графике, выбирая различные точки на оси x и находя их соответствующее изображение через функцию, чтобы облегчить процесс нахождения функции график функции .

Квадратичная формула

Является ли квадратичная формула связанных с графиком квадратичной функции? Еще бы! С геометрической точки зрения, при решении квадратного уравнения

\[a x^2 + bx + c = 0 \]

вы получите корни квадратного уравнения, а когда корни действительны, они представляют собой точки, в которых парабола пересекает ось x.

Особый случай имеет место, когда корни комплексные, в этом случае парабола не пересекает ось x.

Типы квадратичных графиков

Как мы уже говорили, ВСЕ одномерные квадратичные функции будут представлены параболами, но в зависимости от того, a > 0 или a < 0, параболы будут раскрываться вверх или вниз соответственно.

Другое различие типов парабол может быть для тех, которые "центрированы" (т.е вершина это происхождение), и те, которые не являются таковыми.

Пример: квадратичный график

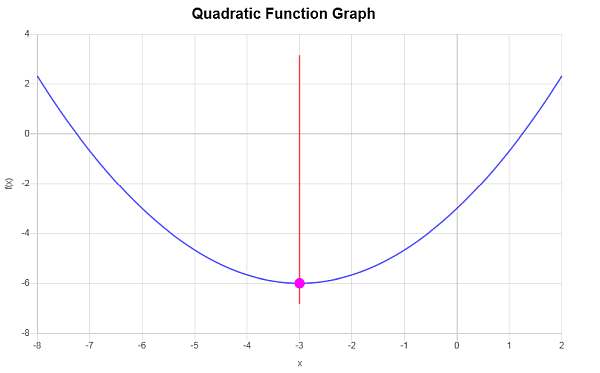
Постройте график : \(f(x) = \frac{1}{3}x^2 +2x - 3\)

Решение:

Нам необходимо построить график заданной квадратичной функции \(f(x) = \displaystyle \frac{1}{3}x^2+2x-3\). Также будут вычислены координаты вершины.

Для квадратичной функции вида \(f(x) = a x^2 + bx + c\) координата x вершины вычисляется по следующей формуле:

\[x_V = \displaystyle -\frac{b}{2a}\]

В этом случае мы имеем, что функция, для которой нам нужно найти вершину, равна \(f(x) = \displaystyle \frac{1}{3}x^2+2x-3\), из чего следует, что соответствующие коэффициенты являются:

\[a = \frac{1}{3}\] \[b = 2\] \[c = -3\]

Подставляя известные значения \(a\) и \(b\) в формулу для x-координаты вершины, получаем:

\[x_V = \displaystyle -\frac{b}{2a} = \displaystyle -\frac{2}{2 \cdot \frac{1}{3}} = -3\]

Теперь нам нужно подставить значение \(x_V = \displaystyle -3\) в квадратичную функцию, чтобы получить:

\[y_V = f(x_V)\] \[ = \frac{1}{3}\cdot \left(-3\right)^2+2\cdot \left(-3\right)-3=\frac{1}{3}\cdot \left(-3\right)^2+2\cdot \left(-3\right)-3=9\cdot\frac{1}{3}-6-3=3-6-3=-6\]

Таким образом, координата x вершины равна \(x_V = \displaystyle -3\), а координата y вершины равна \(y_V = \displaystyle -6\). Это означает, что точка, обозначающая вершину, равна \( \displaystyle \left(-3, -6\right)\).

Графически получается следующее:

Пример: квадратичный график

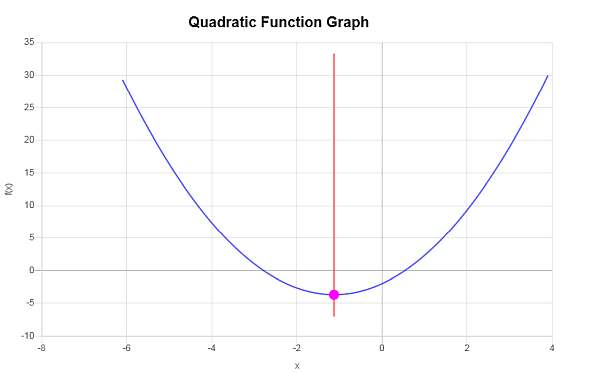
График: \(f(x) = \frac{4}{3}x^2 +3x - 2\), какой это тип квадратичного графика?

Отвечать: В этом случае мы имеем, что функция, для которой нам нужно найти вершину, равна \(f(x) = \displaystyle \frac{4}{3}x^2+3x-2\), из чего следует, что соответствующие коэффициенты являются:

\[a = \frac{4}{3}\] \[b = 3\] \[c = -2\]

Подставляя известные значения \(a\) и \(b\) в формулу для x-координаты вершины, получаем:

\[x_V = \displaystyle -\frac{b}{2a} = \displaystyle -\frac{3}{2 \cdot \frac{4}{3}} = -\frac{9}{8}\]

Теперь нам нужно подставить значение \(x_V = \displaystyle -\frac{9}{8}\) в квадратичную функцию, чтобы получить:

\[y_V = f(x_V)\] \[ = \frac{4}{3}\cdot \left(-\frac{9}{8}\right)^2+3\cdot \left(-\frac{9}{8}\right)-2=\frac{4}{3}\cdot\frac{81}{64}+3\cdot \left(-\frac{9}{8}\right)-2=\frac{27}{16}-\frac{27}{8}-2=-\frac{59}{16}\]

Таким образом, координата x вершины равна \(x_V = \displaystyle -\frac{9}{8}\), а координата y вершины равна \(y_V = \displaystyle -\frac{59}{16}\). Это означает, что точка, обозначающая вершину, равна \( \displaystyle \left(-\frac{9}{8}, -\frac{59}{16}\right)\).

Графически получается следующее:

Больше квадратичных калькуляторов

Большинство всех приложений в базовой алгебре основаны на решении некоторого рода Квадратное уравнение , поэтому у него есть сильная педагогическая цель узнать об этом.

квадратичная формула является одним из самых печально известных учебных предметов в математике. Дело не в том, что кубические или квартовые уравнения не существуют, а в том, что квадратные уравнения это те, которые мы можем легко объяснить.