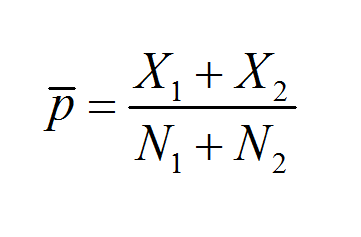Об этом калькуляторе пропорций выборки

С помощью этого калькулятора выборочной пропорции вы сможете предоставить благоприятные случаи и общие случаи, чтобы получить фактическую выборочную пропорцию. Этот процесс широко используется, особенно при проведении опросных анализов.

После того, как вы указали количество благоприятных случаев и общий размер выборки, вам необходимо нажать кнопку "Рассчитать", чтобы получить результаты и интерпретацию расчетов.

Пропорции выборки являются важнейшим понятием в статистике, поскольку пропорцию выборки можно рассматривать как фактическое среднее значение n переменных Бернулли(p), поэтому Центральная предельная теорема применяется, когда размер выборки достаточно велик (\(n \ge 30\)).

Это, с практической точки зрения, означает, что мы можем использовать нормальное распределение для вычислить пропорциональные вероятности .

Что представляет собой пропорция выборки?

Пропорция выборки, определяемая как благоприятные случаи, деленные на общее число случаев, представляет собой ту долю, которая есть у группы по отношению к общему числу случаев. В терминах формулы мы имеем следующее:

\[ \hat p = \displaystyle \frac{ \text{Favorable Case} }{ \text{ Total Cases} } = \displaystyle \frac{X}{N} \]

Например, доля выборки 0,55 указывает на то, что число благоприятных случаев составляет 55% от общего числа случаев, что дает нам очень хорошее представление о размере одной конкретной группы по отношению к общему числу случаев.

Каковы шаги для определения пропорции выборки?

• Шаг 1: Определите количество благоприятных случаев (X) и общее количество случаев (N)
• Шаг 2: Вы можете продолжить только в том случае, если и благоприятные случаи, и общее количество случаев являются целыми числами, и количество благоприятных случаев не превышает общего количества случаев
• Шаг 3: Вы используете формулу \(\hat p = \displaystyle \frac{X}{N}\)
• Шаг 4: Вы можете умножить пропорцию выборки \(\hat p\) на 100, чтобы получить соответствующий процент

Выборка пропорции имеет решающее значение при проведении анализа опросов в ходе избирательного процесса, где подходящая выборка может привести к раннему прогнозированию победителя. Выборочная пропорция является только точечным оценщиком, и для проведения выводных утверждений необходимо найти доверительный интервал для выборочной доли .

Что такое символ пропорции выборки?

Символ выборочной пропорции традиционно \(\hat p\), что, очевидно, исходит из того факта, что это оценка истинной пропорции популяции \(p\). Некоторые учебники будут использовать обозначение вроде \(\hat{\pi}\), но оно встречается сравнительно редко.

Идея использования специального символа кажется излишней, но если бы нам пришлось писать длинную форму "пропорции образца" каждый раз, когда нам нужно к ней обратиться, это стало бы действительно громоздким, и существование четкого, недвусмысленного символа оказалось бы весьма кстати.

Зачем иметь дело с пропорциями выборки

Поскольку зачастую мы не знаем, какова фактическая доля населения, работа с выборочными данными представляется хорошим вариантом, особенно если процесс выборки был случайным и в идеале репрезентативным для всей популяции.

В силу Теорема Чебышева , то пропорция выборки будет сходиться к истинной пропорции популяции, и тогда мы получим превосходное приближение истинной информации о популяции.

Пример

В ходе голосования в общественном клубе было обнаружено, что в голосовании приняли участие N = 120 членов, из которых X = 65 проголосовали за кандидата А. Какой процент избирателей в клубе отдают предпочтение кандидату А?

Решение: Пропорция выборки составляет

\[ \hat p = \displaystyle \frac{ \text{Favorable Case} }{ \text{ Total Cases} } = \displaystyle \frac{65}{120} = 0.5417 \]

Это означает, что 54,17% избирателей клуба отдают предпочтение кандидату А. На этом расчеты завершаются.

Больше статистических калькуляторов

Использование выборочных распределений для пропорции приводит к тому, что нормальные вероятности может быть использовано, что является большим преимуществом, и тем более, когда его можно использовать на уровне нормальное распределение выборки , где изменчивость уменьшается в \(\sqrt n\) раз.

Пропорции выборки также являются основным ингредиентом доверительные интервалы для пропорций и z-тест для пропорций .