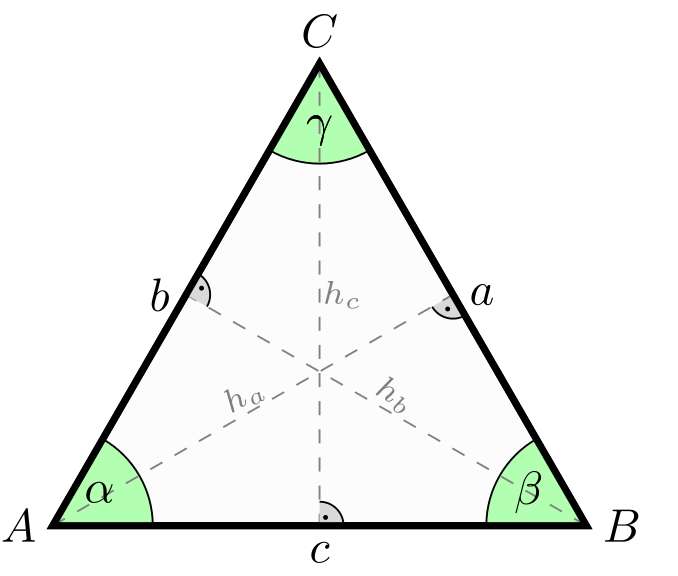
Perimeter of a Triangle

Use this calculator if you need to find the perimeter of a triangle given its three sides. These sides can be simple numbers, or you can define any valid numerical expressions such as "sqrt(3)" or "3/4", just to mention a few.

Then, after the three sides are provided, with three valid numerical expressions or values, you can click on "Calculate" to gets the steps of the simplification shown to you.

How do you Calculate the Perimeter of a Triangle?

Calculating the perimeter of a triangle is very simple, and it involves adding the lengths of all three sides. Here are the steps:

• Identify the length of each side of the triangle.
• If the sides are given implicitly and require further steps for calculation, do so.
• Add these lengths together so to find the total perimeter.

Here is an example:

Suppose a triangle has sides of 5 cm, 7 cm, and 9 cm, you would calculate the perimeter as follows:

\(5 + 7 + 9 = 21\) cm

Perimeter of a Triangle Formula

The formula for the perimeter of a triangle is quite simple:

\[P = a + b + c\]

where:

• P is the perimeter
• a, b, and c represent the lengths of the sides of the triangle

Perimeter of Different Types of Triangles

There are different types of situations you could find that could lead to specific calculations, depending of the type of triangle you are given. The most typical case is the case of an scalene triangle, in which not much symmetry is had.

But also we can find cases where different types of symmetry can be found, for which you don't need to have all three angles and you can calculate the perimeter with less information.

Perimeter of an Equilateral Triangle

An equilateral triangle is a type of triangle that has all sides of equal length and all angles with the same measure. The formula simplifies to:

\[P = 3s\]

where s is the length of one side, which is common to the other sides.

Perimeter of an Isosceles Triangle

An isosceles triangle has two sides of equal length. In this case, if the equal sides are s and the base is b, the perimeter is:

\[P = 2s + b\]

Perimeter of a Scalene Triangle

For an scalene triangle which has all sides of different lengths we need to use the general formula:

\[P = a + b + c\]

Perimeter of a Right Triangle

For a right triangle, you can use the Pythagorean theorem to find the missing side if needed, then apply the perimeter formula:

\[P = a + b + c\]

where we would have something like \(c = \sqrt{a^2+b^2}\), which indicates that the perimeter could be computed off \(a\) and \(b\)

Examples of Perimeter Calculations

Example: Calculating the perimeter of a Triangle with Known Sides

Consider a triangle with sides of 10 cm, 12 cm, and 15 cm. The perimeter is equal to:

\(P = 10 + 12 + 15 = 37\) cm

Example: Finding the Missing Side of a Triangle

If you know two sides and the perimeter, you can find the third side. For instance, if you know that the perimeter is 25 cm and two sides are 8 cm and 10 cm:

\[P = 8 + 10 + x = 25\]

Now, we solve for \(x\):

\(x = 25 - 18 = 7\) cm

Why is Perimeter Important in Real Life?

There are zillion of practical cases in which the perimeter of a triangle plays an important tole:

• Construction: Useful when laying out foundations or framing structures.
• Landscaping: Fundamental for the purpose of determining the amount of fencing needed.
• Art and Design: It is a strong parameter for the creation of symmetrical or balanced compositions.

Common Mistakes When Calculating Perimeter

There are some points where students have a tendency to make mistakes. Here are some of the most common errors to avoid:

• Make sure to account for all sides of the triangle.
• Use the correct formula. Unless you know a specific situation with symmetry, use the most common formula with the sum of the side lengths.
• Be careful in the way you use and interpret the results from the Pythagorean theorem.

Triangle Calculators

Understanding the perimeter of a triangle is just the beginning. If you're interested in exploring more about triangles, you might find it useful to calculate the area of a triangle. This can help in understanding the relationship between the sides and angles, providing a more comprehensive view of the triangle's properties.

Additionally, for a more detailed analysis, our triangle calculator can assist in solving various triangle problems, including finding unknown sides or angles when some are known. If you're dealing specifically with triangles where all three sides are known, our triangle calculator with three sides known will be particularly handy.