More on this this Isosceles Triangle Calculator

This calculator will allow you to solve an isosceles triangle after you provide the size of the equal sides and the apex angle encompassed by these two sides.

After you have provided that information, all that is left for you to do is to click "Calculate" to the solution, step-by-step, shown to you.

What is an Isosceles Triangle?

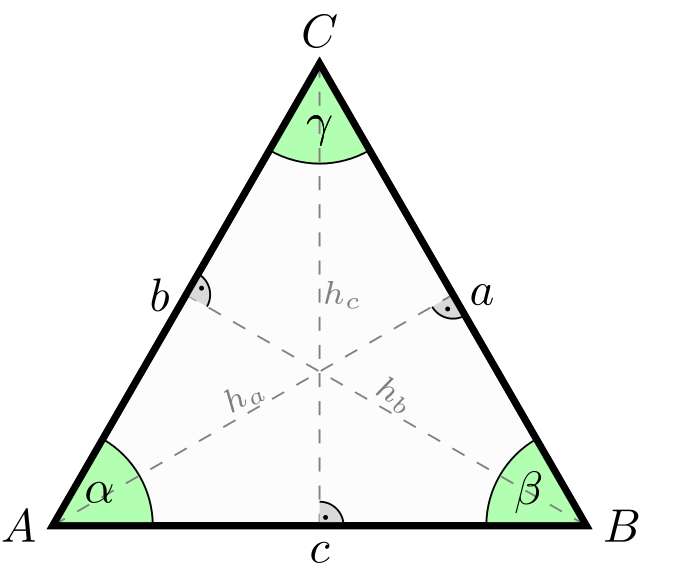
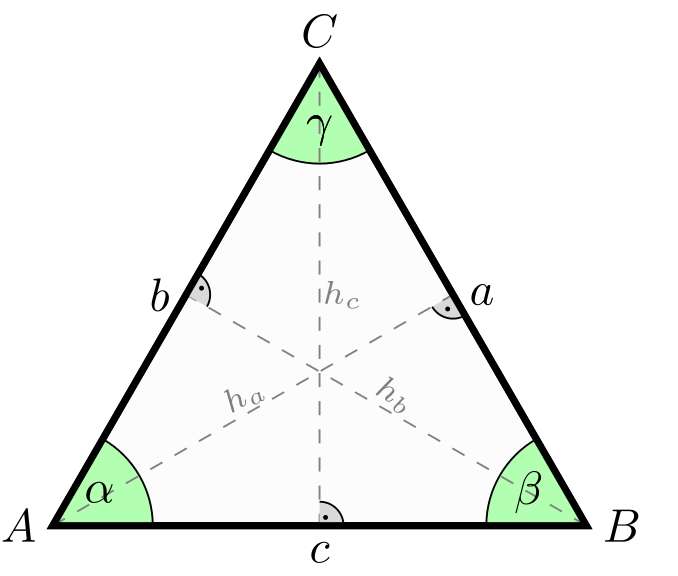
An isosceles triangle is a type of triangle where at least two sides are of equal length. This equality of sides leads to some unique properties and formulas that are essential for calculations involving this type of triangular shape.

Understanding these properties is key to doing isosceles triangle calculations effectively, due to the symmetry found in them, where not only two sides are equal but also two angles must be equal as a consequence.

How to Calculate Isosceles Triangles?

Calculating isosceles triangles involves several steps, depending on what elements you need to find:

Steps to Calculate Area and Perimeter

• Identify the base and the sides that are equal. Usually this directly provided in the the setting.
• Use the formula for area: \( \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} \) Here you need to compute the base and height from the repeated side and the apex angle.
• Calculate the perimeter by summing all sides: \( \text{Perimeter} = \text{base} + 2 \times \text{equal side} \).

Naturally, these formulas require for you to have already calculated all three sides and all three angles, as well as having computed the height, either by using Pythagoras theorem or a trigonometric expressions

Isosceles Triangle Formulas for Area and Perimeter

The formulas for an isosceles triangle are straightforward, but they do require for you to have calculated the other side, which plays the role of the base and the height. Both of those could be computed using the known apex angle \(\theta\) and the repeated size \(s\), using the following

• Base (\(b\)): \( \sin\left(\frac{\theta}{2}\right) = \frac{b/2}{s} \), which implies that \(b = 2s \sin\left(\frac{\theta}{2}\right)\)
• Height (\(h)): \( \cos\left(\frac{\theta}{2}\right) = \frac{h}{s} \), which implies that \(h = 2s \cos\left(\frac{\theta}{2}\right)\)

This goes to show that base and height are directly computed in terms of apex angle \(\theta\) and the repeated size length \(s\)

Isosceles Triangle Theorem Explained

The isosceles triangle theorem states that if two sides of a triangle are equal, then the angles opposite those sides are also equal. This theorem is fundamental for understanding the symmetry in isosceles triangles.

It also plays an operational important role by sizeably reducing the number of calculations required to fully compute the triangle (meaning, all three sides and three angles)

Golden Triangle Calculator

A golden triangle is a special isosceles triangle where the ratio of the sides is the golden ratio, approximately \(\varphi = 1.618\), having an apex angle of 72^o, with both basal angles being equal to 362^o.

Here's how you can calculate properties of a golden triangle:

Steps to Calculate Golden Triangle Properties

• Determine the base and the equal sides.
• Use the golden ratio to find the length of the sides: \( \text{side} = \text{base} \times \varphi \), where \( \varphi \) is the golden ratio.
• Calculate the angles using trigonometric functions or known properties of the golden triangle.

Is an Isosceles Triangle Always a 45-45-90 Triangle?

No, an isosceles triangle is not always a 45-45-90 triangle. While a 45-45-90 triangle is isosceles, and perhaps one of the most commonly used, not all isosceles triangles have angles of 45 degrees. An isosceles triangle must have two angles that are equal, but they are not necessarily 45 degrees.

The shape of the isosceles triangle will be tightly linked to the size of its basal (equal) angles. Relatively large basal angles are linked to a "spiky" triangle, with a small apex angle. And conversely, relatively small basal angles are linked to a flat isosceles triangle, with a large apex angle

How Do You Find the Third Side of an Isosceles Triangle?

To find the third side of an isosceles triangle:

Steps to Find the Third Side

• Identify the two equal sides.
• Use the Pythagorean theorem if the triangle is right-angled: \( \text{side}^2 + \text{side}^2 = \text{hypotenuse}^2 \).
• If not right-angled, use the Law of Cosines: \( c^2 = a^2 + b^2 - 2ab \cos(C) \), where \( a \) and \( b \) are the equal sides, and \( C \) is the angle between them.

Isosceles Triangle Calculator: Find X

When you need to find an unknown side or angle (often labeled as 'x') in an isosceles triangle:

Steps to Find 'X'

• Identify the known sides or angles.
• Use the isosceles triangle properties or trigonometric functions to solve for 'x'.
• Ensure you're using the correct formula or method based on the given information.

Isosceles Triangle Angle Formula

The sum of the angles in any triangle is 180 degrees. For an isosceles triangle, if the base angles are \( \alpha \), then the vertex angle is \( 180^\circ - 2\alpha \).

On the other hand, if you have available the apex angle \(\theta\), you find that that basal angles are \( (180^\circ - \theta)/2 \)

Isosceles Triangle Calculator for Angles

Calculating angles in an isosceles triangle involves:

Steps to Calculate Angles

• Identify the known angle(s).
• Use the angle sum property to find the unknown angles.
• Apply the isosceles triangle theorem if necessary.

Area of Isosceles Triangle Without Height

If the height is unknown, you can still calculate the area using base and side using:

\[ \text{Area} = \frac{1}{2} \times \text{base} \times \sqrt{\text{side}^2 - \left(\frac{\text{base}}{2}\right)^2} \]

Isosceles Right Triangle Calculator

An isosceles right triangle has two equal sides and a right angle. The existence of a right angle simplifies everything because it allows the use of Pythagoras's Theorem. Here's how to calculate its properties:

Steps to Calculate Properties of an Isosceles Right Triangle

• Identify the hypotenuse or one of the equal sides.
• Use the Pythagorean theorem: \( \text{side}^2 + \text{side}^2 = \text{hypotenuse}^2 \).
• Calculate angles using trigonometric identities or known properties.

FAQs on Isosceles Triangle Calculations

Q: How do you find the area of an isosceles triangle without height?

A: Use the formula \( \text{Area} = \frac{1}{2} \times \text{base} \times \sqrt{\text{side}^2 - \left(\frac{\text{base}}{2}\right)^2} \).

Q: Can an isosceles triangle be a scalene triangle?

A: No, an isosceles triangle has at least two sides equal, while a scalene triangle has all sides different.

Q: What is the difference between an isosceles triangle and an equilateral triangle?

A: An isosceles triangle has at least two sides equal, whereas an equilateral triangle has all three sides equal.

Q: How do you calculate the perimeter of an isosceles triangle?

A: Add the base to twice the length of one of the equal sides: \( \text{Perimeter} = \text{base} + 2 \times \text{equal side} \).

Explore More Triangle Calculators

When dealing with triangles, understanding different configurations can be crucial. If you're working with angles and sides, you might find our Triangle Calculator with two angles and one opposite side particularly useful. This tool helps when you know two angles and the length of the side opposite one of them, providing a comprehensive solution for your triangle calculations.

Another common scenario involves knowing two sides and the angle between them. For this, our Triangle Calculator for Two Sides Known and the Angle between them can be invaluable. It's perfect for when you're dealing with the Side-Angle-Side (SAS) configuration, allowing you to explore the properties of your triangle with ease.

Lastly, if you're interested in a specific type of triangle, our Right Triangle Calculator can provide insights into the unique properties and calculations associated with right triangles, which are fundamental in many geometric and trigonometric problems.