حساب مرونة الطلب السعرية من بيانات العينة

استخدم هذه الآلة الحاسبة لتقدير مرونة الطلب السعرية استنادًا إلى بيانات العينة للسعر والكمية المطلوبة التي تقدمها.

سوف تحتاج إلى تقديم بيانات عينة صالحة, من حيث كون كل من العينتين (السعر والكمية المطلوبة) قيمتين موجبتين. بمجرد لصق بياناتك في جدول البيانات, يمكنك النقر فوق "حساب" للحصول على جميع الخطوات الموضحة.

لاحظ أن هذا النهج يتطلب أن تتبع البيانات نمطًا محددًا يناسب نموذج السجل-السجل, حيث يتم استخدام \(\ln(P)\) و \(\ln(Q)\) كمتغيرات مساعدة لإجراء نموذج الانحدار الخطي.

حساب مرونة السعر من بيانات العينة

لكي تحسب مرونة السعر, سوف تحتاج إلى تقدير النموذج المساعد التالي:

\[\displaystyle \ln(Q) = a + b \ln(P) \]

لاحظ أن هذا يتوافق مع نموذج الانحدار الخطي المنتظم حيث يتم تحويل المتغيرين الأصليين السعر والكمية إلى لوغاريتم. ولهذا السبب نطلب أن يكون كلا المتغيرين موجبين تمامًا.

ما هي خطوات حساب المرونة؟

• الخطوة 1: تحديد بيانات العينة للمتغيرات المقدمة للسعر (P) والكمية (Q)
• الخطوة 2: تأكد من أن كلتا العينتين تحتويان على حجم العينة وأن كلاهما إيجابيان, وإلا فلن تتمكن من إجراء الحساب
• الخطوه 3: تحويل اللوغاريتم لكلا المتغيرين: احسب ln(X) وln(Y)
• الخطوة 4: قم بإجراء انحدار خطي مساعد للمتغيرات ln(X) وln(Y), حيث ln(X) هو المتغير المستقل وln(Y) هو المتغير التابع
• الخطوة 5: معامل الانحدار الذي تم العثور عليه لهذا الانحدار المساعد هو مرونة السعر للطلب على هذه البيانات

الخطوة الحاسمة هنا هي تحويل البيانات إلى لوغاريتم, وهو ما يسمح لنا بحساب المرونة على أساس نتائج الانحدار الخطي, مما يجعل النتائج التي توصلنا إليها قابلة للتفسير بدرجة كبيرة.

فهم مرونة الأسعار

حسب التعريف, يتم تعريف مرونة السعر باستخدام الصيغة التالية:

\[ \varepsilon = \displaystyle \frac{\% \Delta Q }{\% \Delta P} \]

ويشير هذا إلى أنه, من بين أمور أخرى, يمكننا التنبؤ بنسبة التغير في كمية الطلب باستخدام التعبير التالي:

\[ \% \Delta Q = \varepsilon \cdot \% \Delta P \]

يشير هذا إلى أن النسبة المئوية للتغير في Q تساوي النسبة المئوية للتغير في P مضروبة في المرونة. ومن المهم ملاحظة أن هذا التعريف ينطبق نقطة بنقطة :هذا يعني أن المرونة لا يجب أن تكون ثابتة طوال منحنى الطلب. على الرغم من أنها قد تكون كذلك, وفي هذه الحاسبة يتم افتراض ذلك.

تفسير معاملات مرونة السعر

كما رأينا في القسم السابق, فإن المرونة \(\varepsilon\) تتوافق ببساطة مع معامل ميل الانحدار المحول باللوغاريتم المساعد. ولكن أيضًا, لديها تفسير مثير للاهتمام للغاية للتغير الهامشي:

• بالنسبة للتغير الإضافي بنسبة 1% في السعر, تتغير كمية الطلب بمقدار \(\varepsilon \%\)

وهذا هو بالضبط ما تتطلبه صيغة المرونة وما تعنيه. لاحظ أن هذه الآلة الحاسبة تقدر نموذجًا يفترض أن البيانات تتبع نمطًا يفضي إلى مرونة ثابتة, وهو ما لا ينطبق على دالة الطلب الخطية على سبيل المثال.

العوامل المؤثرة على مرونة الأسعار

المرونة هي انعكاس لرد فعل المستهلكين تجاه التغيرات في الأسعار. وعادة ما تكون المرونة سلبية: إذا ارتفع سعر سلعة ما, فمن المرجح أن يشتري المشتري كميات أقل, على الأقل إذا كانت لدينا سلعة عادية.

يقال أن المرونة الأكبر من 1 في القيمة المطلقة (أقل من -1) مرتبطة برد فعل مرن على السعر, بينما يقال أن المرونة بين 0 و1 في القيمة المطلقة (بين -1 و0) مرتبطة برد فعل غير مرن على السعر.

تتنبأ نظرية الاقتصاد بأن عوامل مختلفة ستؤثر على مرونة الطلب السعرية. على سبيل المثال, سيؤدي غياب البدائل أو نقصها إلى مرونة أكبر في القيم المطلقة.

حساب مرونة العينة: استخدام بيانات العينة

احسب المرونة من بيانات العينة التالية:

ص	س
1	10
2	13.4
3	15.8
4	21.2
5	26.7
6	40.1

المحلول :من أجل إيجاد مرونة الطلب السعرية من هذه البيانات, نحتاج إلى إنشاء نموذج انحدار لوغاريتمي, حيث يكون المتغير المستقل الذي سنستخدمه هو \(ln(P)\), والمتغير التابع هو اللوغاريتم الطبيعي لـ \(ln(Q)\)

من أجل حساب معاملات الانحدار لهذا الانحدار المساعد, يجب استخدام الجدول التالي:

	ص	ز = ل ن (ص)	س	و = ل ن (س)	\(Z \cdot W\)	\(Z^2\)	\(W^2\)
	1	0	10	2.303	0	0	5.302
	2	0.69	13.4	2.595	1.8	0.48	6.735
	3	1.1	15.8	2.76	3.03	1.21	7.618
	4	1.39	21.2	3.054	4.23	1.92	9.327
	5	1.61	26.7	3.285	5.29	2.59	10.789
	6	1.79	40.1	3.691	6.61	3.21	13.626
Sum =	21	6.58	127.2	17.688	20.97	9.41	53.397

بناءً على الجدول أعلاه, يتم حساب ما يلي:

\[\bar Z = \frac{1}{n} \sum_{i=1}^{n} Z_i = \frac{ 6.579}{ 6} = 1.097\]\[\bar W = \frac{1}{n} \sum_{i=1}^{n} Y_i = \frac{ 17.688}{ 6} = 2.948\] \[\large SS_{ZZ} = \sum_{i=1}^{n} Z_i^2 - \displaystyle\frac{1}{n}\left(\sum_{i=1}^{n} Z_i\right)^2 = 9.41 - 6.579^2/6 = 2.195\] \[\large SS_{WW} = \sum_{i=1}^{n} W_i^2 - \displaystyle\frac{1}{n}\left(\sum_{i=1}^{n} W_i\right)^2 = 53.397 - 17.688^2/6 = 1.254\] \[\large SS_{ZW} = \sum_{i=1}^{n} Z_i W_i - \displaystyle\frac{1}{n}\left(\sum_{i=1}^{n} Z_i\right) \left(\sum_{i=1}^{n} W_i\right) = 20.965 - 6.579 \times 17.688/6 = 1.57\]

لذلك, بناءً على الحسابات المذكورة أعلاه, يتم الحصول على معاملات الانحدار (الميل \(m\), والتقاطع مع المحور y \(n\)) على النحو التالي:

\[m = \frac{SS_{ZW}}{SS_{ZZ}} = \frac{ 1.57}{ 2.195} = 0.715\]\[n = \bar W - \bar Z \cdot m = 2.948 - 1.097 \times 0.715 = 2.1639\]

وبالتالي نجد أن معادلة الانحدار هي:

\[W = 2.1639 + 0.715 \text{ Z}\]

ولكن بما أن المتغيرات المساعدة هي \(Z = \ln(X)\) و \(W = \ln(Y)\), فإننا نستنتج أن معادلة الانحدار اللوغاريتمي هي:

\[\ln(Q) = 2.1639 + 0.715 \ln(P)\]

لذلك, بناءً على المعلومات المقدمة أعلاه, يتم الحصول على مخطط التشتت ومخطط الانحدار التاليين:

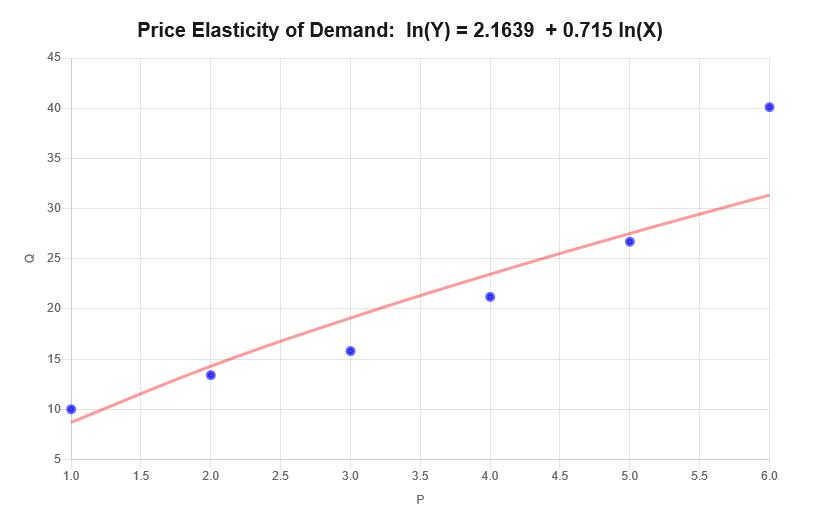
تفسير

تتوافق المرونة في هذه الحالة مع معامل الانحدار للبيانات المقدمة, مما يعني أن \(\varepsilon = 0.715 \), والذي يمكن تفسيره على النحو التالي:

• لزيادة قدرها 1% في السعر, يكون هناك زيادة متوسطة قدرها 0.715% في الكمية المطلوبة.

آلات حاسبة أكثر إثارة للاهتمام

إن تقدير النماذج من بيانات العينة يعد قدرة بالغة الأهمية مطلوبة في كل من الإحصاء والاقتصاد. إن استخدام بيانات العينة حساب نموذج الانحدار يعد أحد التطبيقات الأكثر شيوعًا لاستخدام بيانات العينة لبناء النماذج.

ولكن في كثير من الأحيان, لا يتناسب النموذج الخطي المنتظم مع البيانات بشكل جيد بما فيه الكفاية, ولهذا السبب نحتاج إلى محاولة إنشاء هياكل وظيفية مختلفة. على سبيل المثال, يمكننا تقدير الانحدار اللوغاريتمي , أ الانحدار اللوغاريتمي أو أ الانحدار متعدد الحدود , فقط لذكر بعضها, والتي قد تكون أكثر نجاحًا في تفسير التباين في المتغير التابع من الانحدار العادي.

خيار حساب المرونة من بيانات العينة تُستخدم غالبًا في بيئة استكشافية. في أغلب الأحيان, يتم حساب المرونة مباشرة من دالة الطلب , عندما تكون متاحة. وفي ظروف أخرى, يتم تقدير المرونة من زوج من نقاط السعر والطلب باستخدام صيغة مرونة القوس .