根据样本数据计算需求价格弹性

使用此计算器根据您提供的价格和需求数量样本数据来估算需求价格弹性。

您需要提供有效的样本数据,即两个样本（价格和需求量）均为正值。将数据粘贴到电子表格中后,您可以单击"计算"以获取显示的所有步骤。

请注意,这种方法要求数据遵循适合对数-对数模型的特定模式,其中\(\ln(P)\)和\(\ln(Q)\)用作辅助变量来建立线性回归模型。

根据样本数据计算价格弹性

为了计算价格弹性,您需要估计以下辅助模型：

\[\displaystyle \ln(Q) = a + b \ln(P) \]

请注意,这对应于常规线性回归模型,其中原始变量价格和数量经过对数变换。这就是为什么我们要求两个变量都严格为正。

计算弹性的步骤是什么？

• 步骤1： 确定价格（P）和数量（Q）变量的样本数据
• 第2步： 确保两个样本都有样本大小,并且都是正数,否则你将无法进行计算
• 第3步： 对两个变量进行对数变换：计算 ln(X) 和 ln(Y)
• 第4步： 对变量 ln(X) 和 ln(Y) 进行辅助线性回归,其中 ln(X) 是自变量,ln(Y) 是因变量
• 第5步： 该辅助回归的斜率系数是这些数据的需求价格弹性

接下来的关键步骤是对数据进行对数变换,这使我们能够根据线性回归的结果计算弹性,从而使结果具有高度的可解释性。

了解价格弹性

根据定义,价格弹性使用以下公式来定义：

\[ \varepsilon = \displaystyle \frac{\% \Delta Q }{\% \Delta P} \]

这表明,除其他外,我们可以使用以下表达式预测数量需求的百分比变化：

\[ \% \Delta Q = \varepsilon \cdot \% \Delta P \]

这表明 Q 的百分比变化与 P 的百分比变化乘以弹性相同。需要注意的是,此定义适用于 逐点 ：也就是说,弹性不必在整个需求曲线上保持不变。虽然可以,但本计算器中做出了这样的假设。

解释价格弹性系数

正如我们在上一节中看到的,弹性 \(\varepsilon\) 仅对应于辅助对数变换回归的斜率系数。但它也有一个非常有趣的边际变化解释：

• 价格每变动 1%,需求量就会变化 \(\varepsilon \%\)

这正是弹性公式所要求和暗示的。请注意,此计算器估算的模型假设数据遵循有利于恒定弹性的模式,而线性需求函数则并非如此。

影响价格弹性的因素

弹性反映的是消费者对价格变化的反应。弹性通常为负：如果商品价格上涨,买家可能会减少购买,至少对于普通商品而言是如此。

绝对值大于 1（小于 -1）的弹性被认为与价格的弹性反应相关,而绝对值介于 0 和 1 之间（介于 -1 和 0 之间）的弹性被认为与价格的非弹性反应相关。

经济学理论预测不同的因素会影响需求价格弹性。例如,替代品的缺失或短缺将导致绝对值弹性较大。

样本弹性计算：使用样本数据

根据以下样本数据计算弹性：

磷	问
1	10
2	13.4
3	15.8
4	21.2
5	26.7
6	40.1

解决方案 ：为了从这些数据中找到需求价格弹性,我们需要构建一个对数-对数回归模型,其中我们将使用的独立变量是\(ln(P)\),因变量是\(ln(Q)\)的自然对数

为了计算该辅助回归的回归系数,需要使用下表：

	磷	Z = ln(P)	问	W = ln(Q)	\(Z \cdot W\)	\(Z^2\)	\(W^2\)
	1	0	10	2.303	0	0	5.302
	2	0.69	13.4	2.595	1.8	0.48	6.735
	3	1.1	15.8	2.76	3.03	1.21	7.618
	4	1.39	21.2	3.054	4.23	1.92	9.327
	5	1.61	26.7	3.285	5.29	2.59	10.789
	6	1.79	40.1	3.691	6.61	3.21	13.626
Sum =	21	6.58	127.2	17.688	20.97	9.41	53.397

根据上表计算如下：

\[\bar Z = \frac{1}{n} \sum_{i=1}^{n} Z_i = \frac{ 6.579}{ 6} = 1.097\]\[\bar W = \frac{1}{n} \sum_{i=1}^{n} Y_i = \frac{ 17.688}{ 6} = 2.948\] \[\large SS_{ZZ} = \sum_{i=1}^{n} Z_i^2 - \displaystyle\frac{1}{n}\left(\sum_{i=1}^{n} Z_i\right)^2 = 9.41 - 6.579^2/6 = 2.195\] \[\large SS_{WW} = \sum_{i=1}^{n} W_i^2 - \displaystyle\frac{1}{n}\left(\sum_{i=1}^{n} W_i\right)^2 = 53.397 - 17.688^2/6 = 1.254\] \[\large SS_{ZW} = \sum_{i=1}^{n} Z_i W_i - \displaystyle\frac{1}{n}\left(\sum_{i=1}^{n} Z_i\right) \left(\sum_{i=1}^{n} W_i\right) = 20.965 - 6.579 \times 17.688/6 = 1.57\]

因此,根据上述计算,回归系数（斜率\(m\)和 y 截距\(n\)）如下：

\[m = \frac{SS_{ZW}}{SS_{ZZ}} = \frac{ 1.57}{ 2.195} = 0.715\]\[n = \bar W - \bar Z \cdot m = 2.948 - 1.097 \times 0.715 = 2.1639\]

因此,我们发现回归方程为：

\[W = 2.1639 + 0.715 \text{ Z}\]

但由于辅助变量是\(Z = \ln(X)\)和\(W = \ln(Y)\),我们得出结论,对数-对数回归方程为：

\[\ln(Q) = 2.1639 + 0.715 \ln(P)\]

因此,根据上面提供的信息,得到以下散点图和回归图：

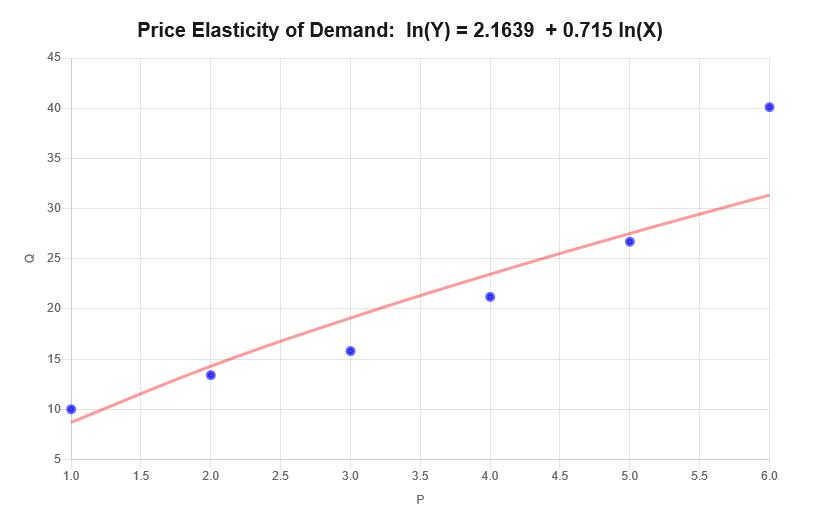
解释

在这种情况下,弹性对应于所提供数据的斜率系数,这意味着\(\varepsilon = 0.715 \),可以解释如下：

• 价格每上涨1%,需求量平均增加0.715%。

更多有趣的计算器

根据样本数据估计模型是统计学和经济学中必备的一项重要能力。利用样本数据来 计算回归模型 是使用样本数据进行模型构建的最常见应用之一。

但通常情况下,常规线性模型不能很好地拟合数据,因此我们需要尝试不同的函数结构。例如,我们可以估计一个 对数-对数回归 ,一个 对数回归 或一个 多项式回归 ,仅举几例,它们比常规回归更能成功解释因变量的变化。

选择 根据样本数据计算弹性 主要用于探索性环境。通常情况下, 弹性直接由需求函数计算得出 （如果有）。在其他情况下,弹性是通过一对价格需求点来估计的,使用 弧弹性公式 .