关于对数-对数模型的更多信息

此计算器可让您针对您提供的数据计算对数-对数回归模型。这些数据需要适当反映对数-对数模型,其中 ln(X) 和 ln(Y) 之间需要有合理的线性关联度。

一旦您提供了有效数据（在本例中意味着 X 和 Y 的正数据）,您将必须单击"计算"按钮开始,以便您可以看到该过程的所有步骤。

对数对数模型具有很强的实际应用,特别是在经济学领域,它用于 计算弹性 .

什么是对数-对数模型？

对数对数模型,顾名思义,是 \(\ln(X)\) 与 \(\ln(Y)\) 表现出显著程度的线性关联的模型。基于这一事实,如果 计算回归模型 对于这些变换数据,我们寻找回归系数\(a\)和\(b\)来估计

\[\displaystyle \ln(Y) = a + b \ln(X)\]

因此,对数-对数模型的计算器简化为对转换后的数据 \(\ln(X)\) 和 \(\ln(Y)\) 的常规回归模型的计算。

估计对数-对数模型的步骤

• 步骤1： 明确识别给定 X 和 Y 的变量。确保它们具有相同的样本大小,并且它们都是正数,否则您无法运行对数对数模型
• 第2步： 将原始数据X和Y变换为辅助ln(X)和ln(x)
• 第3步： 使用常规回归模型方程,计算 坡度 和 Y-截距 对于对数变换数据 ln(X) 和 ln(Y)

一旦估算出了相应的回归系数,就可以写出方程式 \(\displaystyle \ln(Y) = a + b \ln(X)\),可以保留原样,也可以将其转换为：

\[\displaystyle Y = e^a \cdot x^b \]

对数-对数模型解释

我们如何才能像从边际变化的角度对通常的回归进行解释那样解释找到的系数？对于典型的回归问题,斜率系数可以解释为当 X 变量增加一个单位时 Y 变量的平均增量。

在对数对数模型中,它并不完全是这样,但它具有类似的边际解释。事实上,在 \(\displaystyle \ln(Y) = a + b \ln(X)\) 模型中,我们可以将其解释如下：

X 增加 1%,Y 平均增加 b% 。当然,如果是\(b\),这对应的是减少。

我们为什么使用这种模型

一个非常有力的原因是它在经济学中具有广泛的应用。需求价格弹性可以通过计算对数对数模型的斜率系数来找到,这一想法使得它具有足够的相关性,值得考虑。

此外,相对边际变化的概念在经济学中的效用理论中有许多其他应用,使其成为一个极其实用的适用模型。

对数-对数回归计算示例

考虑 X 和 Y 的以下数据：

X：1,2,3,4,5,6,7

Y：10,11.1,13,15.6,16.8,20,22.4

估计相应的对数-对数模型并呈现合适的散点图

解决方案：

这就结束了计算。

更多回归计算器

你需要评估自己是否有 显著相关系数 在运行模型之前,计算 ln(X) 和 ln(Y) 之间的差值。 做一个散点图 看看数据是否与对数-对数关联的预期一致。

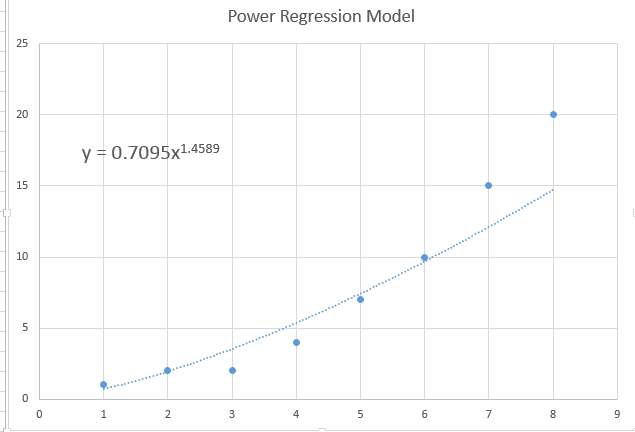
通常情况下,曲率只有很细微的程度,数据会呈现出几乎平坦的模式,这也与传统的回归模型一致,但也可能是一种 幂回归模型 系数非常小...