对数回归计算器的工作原理

该计算器将允许您估算在相应的数据输入电子表格中提供的样本数据的对数回归。

当提供了有效数据（在这种情况下,X 变量只能取正值）后,单击"计算",您将获得该过程中涉及的步骤以及显示拟合质量的散点图。

请注意,当数据在维度上有效时,您始终可以运行对数回归,但这并不意味着结果会是良好的质量,至少在拟合方面是这样。

对数回归的工具和计算器

您可以使用不同的工具来估计对数回归。理论上,您可以手动操作,使用常规计算器（甚至是手机自带的计算器）进行对数转换,然后使用辅助最小二乘方程来找到对数模型,即

\[ Y = a + b \ln(X) + \varepsilon \]

当然,手动操作至少可以说是繁琐且容易出错的。这就是为什么使用这种方法是一个很好的选择 对数回归计算器 因为它为你完成了所有的工作,并向你展示了所有的步骤

还有其他工具,比如手机应用程序,可以进行所有类型的回归,但你需要尝试一下,因为这可能会出现碰运气的情况。

进行对数回归的步骤

• 步骤1： 清晰列出自变量（X）和因变量（Y）,并确保两个变量具有相同的样本量
• 第2步： 确保 X 值为正,否则无法运行回归
• 第3步： 通过应用自然对数变换构造一个新的独立变量 X* = ln(X)
• 第4步： 现在对 X* 与 Y 进行常规线性回归分析

要记住的一件事是,完全建议使用计算器或软件来获取诊断统计数据,这将有助于您评估是否有必要使用 对数回归模型 .

使用 excel 与专用对数回归计算器

Excel 在帮助您进行基本统计分析方面发挥着重要作用：它为您提供了一个干净且经过验证的界面来运行基本测试,包括对数回归的计算。

Excel 的主要问题是它不会为您提供解决方案步骤。这可能有助于 Copilot 等 AI 框架的出现,这些框架可能会赋予 Excel 计算的描述步骤。

理解和解释回归计算器结果

像其他 回归分析 对于对数情况没有什么不同,您将查看模型拟合统计数据,例如 F 统计量 测试模型的整体重要性,以及 预测变量个体重要性的 t 统计量 .

此外,你可能需要查看解释的变化和错误,以及 R^2 和调整后的 R^2 系数 ,它将为您提供模型对因变量解释变化的估计值。

对数回归示例

考虑变量

十：1,2,3,4,5

还有：15,25,28,29,30

估计对数回归模型。

解决方案：

提供 X 和 Y 变量的以下数据来构建对数回归模型：

十	Y
1	15
2	25
3	28
4	29
5	30

我们将使用的独立变量是 X 的自然对数,因变量是 Y。为了计算此辅助回归的回归系数,需要使用下表：

	十	Z = ln(X)	Y	\(Z \cdot Y\)	\(Z^2\)	\(Y^2\)
	1	0	15	0	0	225
	2	0.69	25	17.33	0.48	625
	3	1.1	28	30.76	1.21	784
	4	1.39	29	40.2	1.92	841
	5	1.61	30	48.28	2.59	900
Sum =	15	4.79	127	136.58	6.2	3375

根据上表计算如下：

\[\bar Z = \frac{1}{n} \sum_{i=1}^{n} Z_i = \frac{ 4.787491742782}{ 5} = 0.957\]\[\bar Y = \frac{1}{n} \sum_{i=1}^{n} Y_i = \frac{ 127}{ 5} = 25.4\]\[\large SS_{ZZ} = \sum_{i=1}^{n} Z_i^2 - \displaystyle\frac{1}{n}\left(\sum_{i=1}^{n} Z_i\right)^2 = 6.2 - 4.787^2/5 = 1.615\]\[\large SS_{YY} = \sum_{i=1}^{n} Y_i^2 - \displaystyle\frac{1}{n}\left(\sum_{i=1}^{n} Y_i\right)^2 = 3375 - 127^2/5 = 149.2\]\[\large SS_{ZY} = \sum_{i=1}^{n} Z_i Y_i - \displaystyle\frac{1}{n}\left(\sum_{i=1}^{n} Z_i\right) \left(\sum_{i=1}^{n} Y_i\right) = 136.575 - 4.787 \times 127/5 = 14.973\]

因此,根据上述计算,回归系数（斜率\(m\)和 y 截距\(n\)）如下：

\[m = \frac{SS_{ZY}}{SS_{ZZ}} = \frac{ 14.973}{ 1.615} = 9.2685\] \[n = \bar Y - \bar Z \cdot m = 25.4 - 0.957 \times 9.2685 = 16.5254\]

因此,我们发现回归方程为：

\[\text{ Y} = 16.5254 + 9.2685 \text{ Z}\]

但由于辅助变量\(Z = \ln(X)\),我们得出对数回归方程为：

\[\text{ Y} = 16.5254 + 9.2685 \ln(X)\]

因此,根据上面提供的信息,得到以下散点图和回归图：

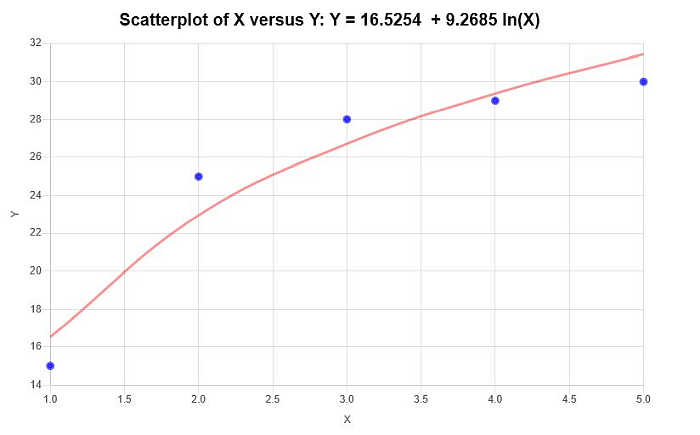
更多统计计算器

您可能还对以下内容感兴趣 计算指数回归 或研究 多项式回归 ,所有这些都适用于不同的情况,基于观察到的样本数据的行为。

你可能想要 构建散点图 为了评估数据的经验行为,并预先评估是否适用对数回归而不是不同类型的回归。