Расчет ценовой эластичности спроса на основе выборочных данных

Используйте этот калькулятор для оценки ценовой эластичности спроса на основе предоставленных вами выборочных данных о цене и объеме спроса.

Вам нужно будет предоставить действительные данные выборки, в том смысле, что обе выборки (цена и требуемое количество) должны быть положительными значениями. После того, как вы вставите данные в электронную таблицу, вы можете нажать "Рассчитать", чтобы получить все показанные шаги.

Обратите внимание, что этот подход требует, чтобы данные следовали определенному шаблону, который подходит для модели двойного логарифма, где \(\ln(P)\) и \(\ln(Q)\) используются в качестве вспомогательных переменных для построения модели линейной регрессии.

Расчет ценовой эластичности на основе выборочных данных

Для расчета ценовой эластичности вам необходимо оценить следующую вспомогательную модель:

\[\displaystyle \ln(Q) = a + b \ln(P) \]

Обратите внимание, что это соответствует обычной линейной регрессионной модели с исходными переменными price и quantity, которые были преобразованы логарифмически. Вот почему мы требуем, чтобы обе переменные были строго положительными.

Каковы шаги для расчета эластичности?

• Шаг 1: Определите выборку данных для переменных, предоставленных для цены (P) и количества (Q)
• Шаг 2: Убедитесь, что оба образца имеют размер выборки и что они ОБА положительные, в противном случае вы не сможете выполнить расчет
• Шаг 3: Логарифмическое преобразование обеих переменных: вычисление ln(X) и ln(Y)
• Шаг 4: Проведите вспомогательную линейную регрессию для переменных ln(X) и ln(Y), где ln(X) — независимая переменная, а ln(Y) — зависимая переменная
• Шаг 5: Коэффициент наклона, найденный для этой вспомогательной регрессии, представляет собой ценовую эластичность спроса для этих данных

Затем решающим шагом становится логарифмическое преобразование данных, которое позволяет нам вычислить эластичность на основе результатов линейной регрессии, что делает полученные результаты легко интерпретируемыми.

Понимание ценовой эластичности

По определению ценовая эластичность определяется с помощью следующей формулы:

\[ \varepsilon = \displaystyle \frac{\% \Delta Q }{\% \Delta P} \]

Это указывает на то, что, помимо прочего, мы можем предсказать процентное изменение количественного спроса, используя следующее выражение:

\[ \% \Delta Q = \varepsilon \cdot \% \Delta P \]

Это означает, что процентное изменение Q равно процентному изменению P, умноженному на эластичность. Важно отметить, что это определение применимо точечно : то есть эластичность не обязательно должна быть постоянной на протяжении всей кривой спроса. Хотя может, и в этом калькуляторе такое предположение сделано.

Интерпретация коэффициентов ценовой эластичности

Как мы видели в предыдущем разделе, эластичность \(\varepsilon\) просто соответствует коэффициенту наклона вспомогательной логарифмически преобразованной регрессии. Но также она имеет очень интересную интерпретацию маргинального изменения:

• При дополнительном изменении цены на 1% объем спроса изменяется на \(\varepsilon \%\)

Это именно то, что требуется и подразумевается формулой эластичности. Обратите внимание, что этот калькулятор оценивает модель, которая предполагает, что данные следуют шаблону, который способствует постоянной эластичности, что не относится, например, к линейной функции спроса.

Факторы, влияющие на ценовую эластичность

Эластичность отражает реакцию потребителей на изменение цены. Обычно эластичность отрицательна: если цена товара увеличивается, покупатель, скорее всего, купит меньше, по крайней мере, если у нас нормальный товар.

Говорят, что эластичность больше 1 по абсолютному значению (меньше -1) связана с эластичной реакцией на цену, тогда как эластичность между 0 и 1 по абсолютному значению (между -1 и 0) связана с неэластичной реакцией на цену.

Экономическая теория предсказывает, что различные факторы будут влиять на ценовую эластичность спроса. Например, отсутствие или нехватка заменителей приведет к большей эластичности в абсолютных значениях.

Расчет эластичности образца: использование данных образца

Рассчитайте эластичность на основе следующих выборочных данных:

П	В
1	10
2	13.4
3	15.8
4	21.2
5	26.7
6	40.1

Решение : Чтобы найти ценовую эластичность спроса на основе этих данных, нам необходимо построить модель регрессии в логарифмическом масштабе, где независимой переменной, которую мы будем использовать, будет \(ln(P)\), а зависимой переменной — натуральный логарифм \(ln(Q)\)

Для вычисления коэффициентов регрессии для этой вспомогательной регрессии необходимо использовать следующую таблицу:

	П	Z = ln(P)	В	W = ln(Q)	\(Z \cdot W\)	\(Z^2\)	\(W^2\)
	1	0	10	2.303	0	0	5.302
	2	0.69	13.4	2.595	1.8	0.48	6.735
	3	1.1	15.8	2.76	3.03	1.21	7.618
	4	1.39	21.2	3.054	4.23	1.92	9.327
	5	1.61	26.7	3.285	5.29	2.59	10.789
	6	1.79	40.1	3.691	6.61	3.21	13.626
Sum =	21	6.58	127.2	17.688	20.97	9.41	53.397

На основании приведенной выше таблицы рассчитывается следующее:

\[\bar Z = \frac{1}{n} \sum_{i=1}^{n} Z_i = \frac{ 6.579}{ 6} = 1.097\]\[\bar W = \frac{1}{n} \sum_{i=1}^{n} Y_i = \frac{ 17.688}{ 6} = 2.948\] \[\large SS_{ZZ} = \sum_{i=1}^{n} Z_i^2 - \displaystyle\frac{1}{n}\left(\sum_{i=1}^{n} Z_i\right)^2 = 9.41 - 6.579^2/6 = 2.195\] \[\large SS_{WW} = \sum_{i=1}^{n} W_i^2 - \displaystyle\frac{1}{n}\left(\sum_{i=1}^{n} W_i\right)^2 = 53.397 - 17.688^2/6 = 1.254\] \[\large SS_{ZW} = \sum_{i=1}^{n} Z_i W_i - \displaystyle\frac{1}{n}\left(\sum_{i=1}^{n} Z_i\right) \left(\sum_{i=1}^{n} W_i\right) = 20.965 - 6.579 \times 17.688/6 = 1.57\]

Таким образом, на основании приведенных выше расчетов коэффициенты регрессии (наклон \(m\) и точка пересечения с осью Y \(n\)) получаются следующим образом:

\[m = \frac{SS_{ZW}}{SS_{ZZ}} = \frac{ 1.57}{ 2.195} = 0.715\]\[n = \bar W - \bar Z \cdot m = 2.948 - 1.097 \times 0.715 = 2.1639\]

Таким образом, мы получаем, что уравнение регрессии имеет вид:

\[W = 2.1639 + 0.715 \text{ Z}\]

Но поскольку вспомогательными переменными являются \(Z = \ln(X)\) и \(W = \ln(Y)\), мы приходим к выводу, что уравнение регрессии в двойном логарифме имеет вид:

\[\ln(Q) = 2.1639 + 0.715 \ln(P)\]

Таким образом, на основании предоставленной выше информации получены следующие диаграмма рассеяния и диаграмма регрессии:

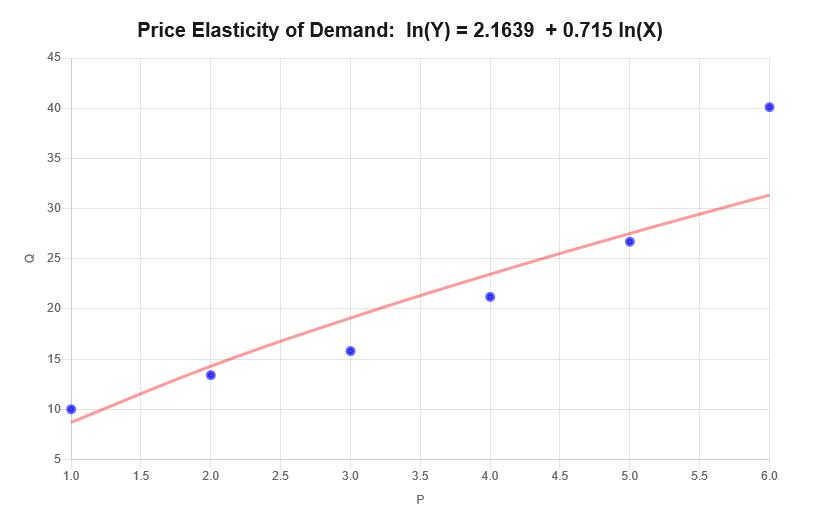
Интерпретация

Эластичность в данном случае соответствует коэффициенту наклона для предоставленных данных, что означает \(\varepsilon = 0.715 \), что можно интерпретировать следующим образом:

• При увеличении цены на 1% средний рост объема спроса составляет 0,715%.

Еще интересные калькуляторы

Оценка моделей на основе выборочных данных является важнейшей способностью, необходимой как в статистике, так и в экономике. Использование выборочных данных для вычислить регрессионную модель является одним из наиболее распространенных применений использования выборочных данных для построения моделей.

Но часто бывает так, что обычная линейная модель не будет соответствовать данным достаточно хорошо, для чего нам нужно попробовать другие функциональные структуры. Например, мы могли бы потенциально оценить Логарифмическая регрессия , а логарифмическая регрессия или Полиномиальная регрессия , и это лишь некоторые из них, которые могли бы быть более успешными при объяснении вариации зависимой переменной, чем обычная регрессия.

Возможность расчет эластичности на основе выборочных данных в основном используется в исследовательской обстановке. Чаще всего, эластичность напрямую вычисляется из функции спроса , когда доступно. В других обстоятельствах эластичность оценивается по паре точек цена-спрос с использованием формула упругости дуги .