More About the Log-Log Model

This calculator will allow you to calculate a log-log regression model for data that you provide. These data needs to a suitable reflection of a log-log model, in which there needs to be a reasonable linear degree of association between ln(X) and ln(Y).

Once you provide a valid data, which in this case means positive data for X and Y, you will have to click on the "Calculate" button to get started so that you can see all the steps of the process.

The log-log model has strong practical applications, especially on the realm of Economics, in which it is use to compute elasticities.

What is the Log-Log Model?

The log-log model, as the name could be suggestive of, is a model in which \(\ln(X)\) exhibits a significant degree of linear association with \(\ln(Y)\). Based on this fact, if become appropriate to calculate a regression model for these transform data, so we look for regression coefficients \(a\) and \(b\) to estimate

\[\displaystyle \ln(Y) = a + b \ln(X)\]

So then, a calculator of a log-log model reduces to a calculation of a regular regression model for the transformed data \(\ln(X)\) and \(\ln(Y)\).

Steps for estimating a Log-Log Model

• Step 1: Clearly identify the variables given X and Y. Make sure they have the same sample size and they BOTH all positive, otherwise you cannot run a log-log model
• Step 2: Transform the original data X and Y into the auxiliary ln(X) and ln(x)
• Step 3: Use a regular regression model equation, where you compute the slope and y-intercept for your log-transformed data ln(X) and ln(Y)

Once you have estimated the corresponding regression coefficients, you can write the equation \(\displaystyle \ln(Y) = a + b \ln(X)\), which you can either leave as it is, or you can transform it as:

\[\displaystyle Y = e^a \cdot x^b \]

Log-Log Model Interpretation

How can we interpret the coefficients found in a way like we have done it with usual regression from a marginal change point of view? For a typical regression problem, you have the the slope coefficient can be interpreted as the average increase in the Y variable when the X variable is increased by one unit.

In a log-log model, it does not work quite like that, but it has a similar marginal interpretation. In fact, in a \(\displaystyle \ln(Y) = a + b \ln(X)\) model, we can interpret it as follows:

An increase of 1% in X bring an average increase in Y of b%. Naturally, if \(b\), this corresponds to a decrease.

Why we use this type of model

One very powerful reason is that it has strong application in Economics. The idea that the price elasticity of demand is simply found by computing the slope coefficient of a log-log model makes it relevant enough to consider it.

Also, the idea of a relative marginal change has many other application in Utility Theory in Economics, making it an extremely practical an applicable model.

Log-Log regression calculation sample

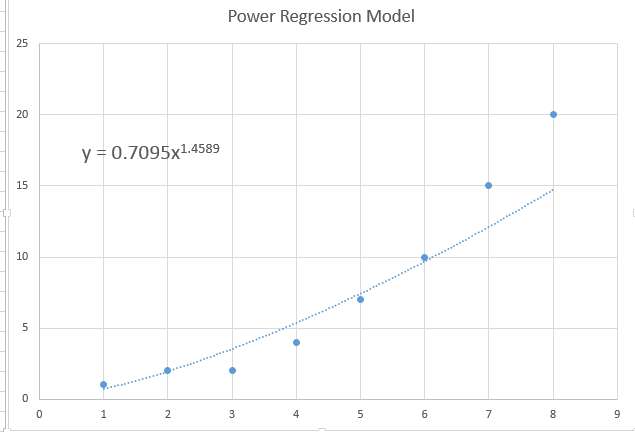
Consider the following data for X and Y:

X: 1, 2, 3, 4, 5, 6, 7

Y: 10, 11.1, 13, 15.6, 16,8, 20, 22.4

Estimate the corresponding log-log model and present a suitable scatterplot

Solution:

which concludes the calculation.

More Regression calculators

You will need to assess whether you have a significant correlation coefficient between ln(X) and ln(Y) before running the model. It is also a good idea to make a scatterplot of the data to see if it is consistent with what is expected from a log-log association.

Often times there is only a subtle level of curvature, and the data will show an almost flat pattern, which is also consistent with a traditional regression model, but it can also be a power regression model with very small coefficients..