द्विघात समीकरण सॉल्वर

यह कैलकुलेटर आपको अनुमति देगा अफ़स्या कि आप प्रदान करते हैं, सभी चरणों को दिखाते हैं।आपको बस एक वैध द्विघात समीकरण प्रदान करने की आवश्यकता है।

यह कुछ ऐसा हो सकता है जो पहले से ही सरल हो और x^2 + 3x + 5 = 0 की तरह हल करने के लिए तैयार हो, आप कुछ प्रदान कर सकते हैं जो आसानी से 3x^2 - 4x + 5/3 = x^2 + 1/3x की तरह सरल नहीं है -1, उदाहरण के लिए।

एक बार जब आप एक मान्य द्विघात समीकरण प्रदान करते हैं, तो आपको बस "गणना" पर क्लिक करने की आवश्यकता है, और आपको गणना करने के लिए प्रक्रिया के सभी चरणों के साथ प्रदान किया जाएगा दthaphak yurण की जड़ें जड़ें वह प्रदान किया गया है।

आमतौर पर, आप द्विघात समीकरणों की गणना करने के लिए द्विघात सूत्र का उपयोग करेंगे, लेकिन यह एकमात्र तरीका नहीं है, जैसा कि हम निम्नलिखित वर्गों में देखेंगे।

एक द्विघात समीकरण की गणना कैसे करें?

द्विघात समीकरणों को हल करने के लिए कई रणनीतियाँ हैं।सबसे अधिक इस्तेमाल किया जाने वाला एक उपयोग है तमाम ।इसके अलावा, आप हल कर सकते हैं अफ़रसी , या आप हल कर सकते हैं तमाम ।

द्विघात सूत्र का उपयोग करके द्विघात समीकरणों की गणना के लिए क्या कदम हैं?

• चरण 1: उस द्विघात समीकरण को पहचानें जिसे आप गणना करना चाहते हैं
• चरण 2: सुनिश्चित करें कि समीकरण पूरी तरह से सरलीकृत है, अन्यथा सरलीकरण के साथ आगे बढ़ें, जब तक कि आपके पास फॉर्म का समीकरण नहीं है, + BX + C = 0
• चरण 3: समीकरण को अपने सरलीकृत रूप में कम करने के बाद, आप द्विघात सूत्र का उपयोग कर सकते हैं: \(x = \displaystyle \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\)

संभवतः, द्विघात समीकरण सूत्र का उपयोग करना एक द्विघात समीकरण की जड़ों को खोजने का सबसे व्यावहारिक तरीका है, लेकिन अन्य कारण हैं कि आप अन्य तरीके क्यों करेंगे।

वर्गों को पूरा करके एक द्विघात समीकरण को कैसे हल करें?

एक द्विघात समीकरण को हल करने का दूसरा सबसे आम तरीका की तकनीक का उपयोग करके है अफ़रसी ।वास्तव में वर्गों को पूरा करने के लिए एक सूत्र नहीं है (हालांकि तकनीकी रूप से एक है, द्विघात समीकरण के समाधान के आधार पर), और यह एक प्रक्रिया है।

वर्गों को पूरा करने के लिए क्या कदम हैं

• चरण 1: उस द्विघात समीकरण को पहचानें जिसे आप हल करना चाहते हैं
• चरण 2: आपको यह सुनिश्चित करने की आवश्यकता है कि समीकरण पूरी तरह से सरलीकृत है, और आपके पास फॉर्म का एक समीकरण है।
• चरण 3: एक उपयुक्त शब्द जोड़ें और घटाना

फॉर्म (x + "कुछ) के एक शब्द की उपस्थिति को मजबूर करने का विचार, जो वर्गों को पूरा करने का अंतिम लक्ष्य है।

आप द्विघात समीकरणों का उपयोग क्यों करेंगे?

द्विघात समीकरण लगातार बीजगणित अनुप्रयोगों में दिखाई देते हैं, शब्द समस्याएं हैं।द्विघात समीकरणों को हल करना एक बुनियादी कोर कौशल है जिसे आपको प्राप्त करने की आवश्यकता है।

फिर, कैलकुलस जैसे क्षेत्रों में, जब अधिकतमकरण और न्यूनतमकरण की समस्याओं की गणना करते हैं, तो आपको सभी प्रकार के द्विघात समीकरणों के साथ अच्छी परिचित होने की आवश्यकता होगी।

उदाहरण: एक द्विघात समीकरण को हल करना

फॉर्मूला का उपयोग करके निम्नलिखित द्विघात समीकरण को हल करें \(4x^2 + \frac{4}{3}x + 2 = 0\)

तमाम: हमें निम्नलिखित दिए गए द्विघात समीकरण को हल करने की आवश्यकता है \(\displaystyle 4x^2+\frac{4}{3}x+2=0\)।

फॉर्म के एक द्विघात समीकरण के लिए \(a x^2 + bx + c = 0\), जड़ों को निम्न सूत्र का उपयोग करके गणना की जाती है:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]

इस मामले में, हमारे पास है कि हमें जिस समीकरण को हल करने की आवश्यकता है, वह है \(\displaystyle 4x^2+\frac{4}{3}x+2 = 0\), जिसका अर्थ है कि संबंधित गुणांक हैं:

\[a = 4\] \[b = \frac{4}{3}\] \[c = 2\]

सबसे पहले, हम जड़ों की प्रकृति का आकलन करने के लिए भेदभाव की गणना करेंगे।भेदभाव की गणना की जाती है:

\[\Delta = b^2 - 4ac = \displaystyle \left( \frac{4}{3}\right)^2 - 4 \cdot \left(4\right)\cdot \left(2\right) = -\frac{272}{9}\]

चूंकि इस मामले में हमें भेदभावपूर्ण लगता है \(\Delta = \displaystyle -\frac{272}{9} < 0\), जो नकारात्मक है, हम जानते हैं कि दिए गए समीकरण में दो अलग -अलग संयुग्मन जटिल जड़ें हैं।

अब, इन मूल्यों को जड़ों के लिए सूत्र में प्लग करना:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{-\frac{4}{3} \pm \sqrt{\left(\frac{4}{3}\right)^2-4\left(4\right)\left(2\right)}}{2\cdot 4} = \displaystyle \frac{-\frac{4}{3} \pm \sqrt{-\frac{272}{9}}}{8}\]

तो फिर, हम पाते हैं कि:

\[\displaystyle x_1 = \frac{-\frac{4}{3} - i \sqrt{\frac{272}{9}}}{8} = -\frac{1}{6} - \frac{1}{6}\sqrt{17} i\] \[\displaystyle x_2 = \frac{-\frac{4}{3} + i \sqrt{\frac{272}{9}}}{8} = -\frac{1}{6} + \frac{1}{6}\sqrt{17} i\]

इसलिए, दिए गए समीकरण \(\displaystyle 4x^2+\frac{4}{3}x+2=0\) में दो अलग -अलग संयुग्मन जटिल जड़ें हैं, जो \(x_1 = \displaystyle -\frac{1}{6} - \frac{1}{6}\sqrt{17} i\) और \(x_2 = \displaystyle -\frac{1}{6} + \frac{1}{6}\sqrt{17} i\) हैं।

रेखांकन:

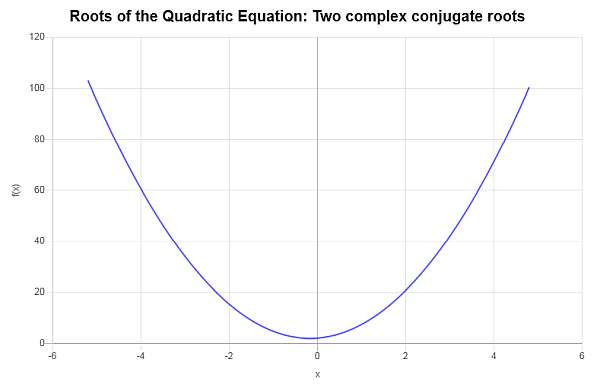
उदाहरण: एक द्विघात समीकरण की जड़

वर्गों को पूरा करके निम्नलिखित द्विघात समीकरण की जड़ों का पता लगाएं \(2x^2 + \frac{1}{3}x + \frac{1}{72} = 0\)

तमाम: इस मामले में, हमारे पास है कि हमें जिस समीकरण को हल करने की आवश्यकता है, वह है \(\displaystyle 2x^2+\frac{1}{3}x+\frac{1}{72} = 0\), जिसका अर्थ है कि संबंधित गुणांक हैं:

\[a = 2\] \[b = \frac{1}{3}\] \[c = \frac{1}{72}\]

भेदभाव की गणना की जाती है:

\[\Delta = b^2 - 4ac = \displaystyle \left( \frac{1}{3}\right)^2 - 4 \cdot \left(2\right)\cdot \left(\frac{1}{72}\right) = 0\]

चूंकि इस मामले में हमें भेदभावपूर्ण लगता है \(\Delta = \displaystyle 0 = 0\), जो शून्य है, हम जानते हैं कि समीकरण में केवल एक वास्तविक जड़ है।

अब, इन मूल्यों को जड़ों के लिए सूत्र में प्लग करना:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{-\frac{1}{3} \pm \sqrt{\left(\frac{1}{3}\right)^2-4\left(2\right)\left(\frac{1}{72}\right)}}{2\cdot 2} = \displaystyle \frac{-\frac{1}{3} \pm \sqrt{0}}{4}\]

तो फिर, हम पाते हैं कि:

\[x = \displaystyle \frac{-\frac{1}{3}}{4} = \displaystyle -\frac{1}{12}\]

इसलिए, दिए गए समीकरण \(\displaystyle 2x^2+\frac{1}{3}x+\frac{1}{72}=0\) में केवल एक वास्तविक जड़ है, जो \(x = \displaystyle -\frac{1}{12}\) है।

रेखांकन:

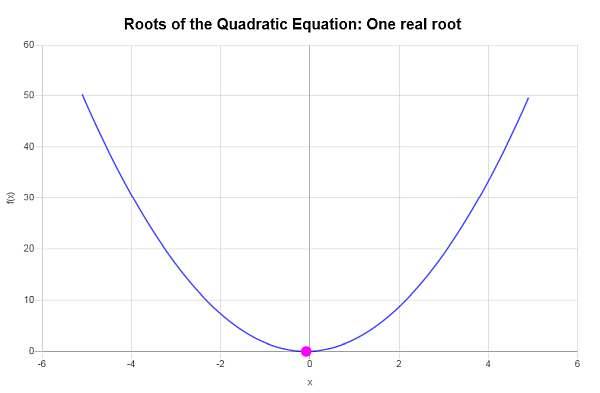
उदाहरण: समीकरण गणना की जड़ें

निम्नलिखित को हल करें: \(3x^2 + \frac{2}{3}x - \frac{4}{3} = 0\)

तमाम: इस उदाहरण के लिए हमें जिस समीकरण को हल करने की आवश्यकता है, वह है \(\displaystyle 3x^2+\frac{2}{3}x-\frac{4}{3} = 0\), तो फिर संबंधित गुणांक हैं:

\[a = 3\] \[b = \frac{2}{3}\] \[c = -\frac{4}{3}\]

इस मामले में, भेदभाव की गणना की जाती है:

\[\Delta = b^2 - 4ac = \displaystyle \left( \frac{2}{3}\right)^2 - 4 \cdot \left(3\right)\cdot \left(-\frac{4}{3}\right) = \frac{148}{9}\]

चूंकि भेदभावपूर्ण \(\Delta = \displaystyle \frac{148}{9} > 0\) है, जो सकारात्मक है, हम जानते हैं कि समीकरण में दो अलग -अलग वास्तविक जड़ें होंगी।

अब, इन मूल्यों को जड़ों के लिए सूत्र में प्लग करना:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{-\frac{2}{3} \pm \sqrt{\left(\frac{2}{3}\right)^2-4\left(3\right)\left(-\frac{4}{3}\right)}}{2\cdot 3} = \displaystyle \frac{-\frac{2}{3} \pm \sqrt{\frac{148}{9}}}{6}\]

तो फिर, हम पाते हैं कि:

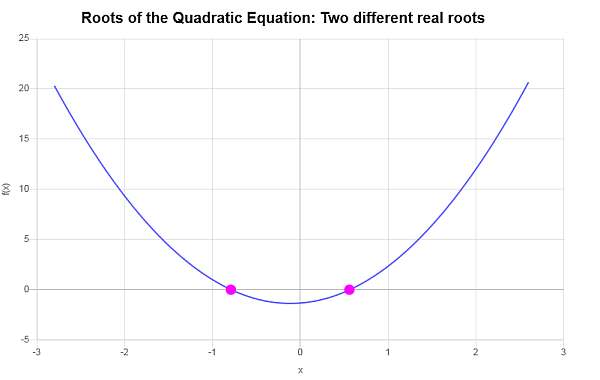
\[ x_1 = -\frac{\frac{2}{3}}{6}-\frac{1}{6}\sqrt{\frac{148}{9}}=-\frac{1}{9}\sqrt{37}-\frac{1}{9} \] \[x_2 = -\frac{\frac{2}{3}}{6}+\frac{1}{6}\sqrt{\frac{148}{9}}=\frac{1}{9}\sqrt{37}-\frac{1}{9}\]

इसलिए, दिए गए समीकरण \(\displaystyle 3x^2+\frac{2}{3}x-\frac{4}{3}=0\) की दो अलग -अलग वास्तविक जड़ें हैं, जो \(x_1 = \displaystyle -\frac{1}{9}\sqrt{37}-\frac{1}{9}\) और \(x_2 = \displaystyle \frac{1}{9}\sqrt{37}-\frac{1}{9}\) हैं।

रेखांकन:

अन्य उपयोगी द्विघात कैलकुलेटर

जैसा कि हमने इस ट्यूटोरियल में देखा है, अफ़रसी द्विघात समीकरणों की गणना में एक मौलिक भूमिका निभाता है।इसके अलावा, आप इसका उपयोग कर सकते हैं विभेदक कैलकुलेट समीकरण को हल किए बिना जड़ों की प्रकृति (दो वास्तविक जड़ें, एक वास्तविक जड़, या दो जटिल जड़ें) का आकलन करने के लिए।

आप इसका उपयोग भी कर सकते हैं सराय एक द्विघात समीकरण के शीर्ष के निर्देशांक को खोजने के लिए, और अफ़रदा नारी ।इसके अलावा आप इसका पता लगा सकते हैं तमाम द्विघात समीकरणों की गणना करने के एक और तरीके का पता लगाने के लिए उपकरण।