Уравнение окружности
Круг - одна из самых примечательных геометрических фигур. Она обладает замечательной симметрией, основанной на том, что ВСЕ точки круга равноудалены от центра, что в переводе с английского означает, что все точки круга находятся на одинаковом расстоянии от центра. Это общее расстояние \(r\) называется радиус окружности .
Круг имеет множество важных геометрических применений, что делает его действительно важным объектом как в геометрии, так и в алгебре.
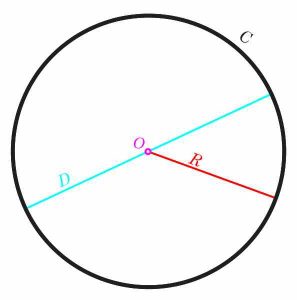
Еще одним важнейшим свойством окружности является то, что ее очень легко представить алгебраически. Это означает, что мы можем легко задать уравнение, которое будет представлять все точки данной окружности. Чтобы выразить это более конкретно, рассмотрим координатную плоскость \(X - Y\). Это означает, что оси X и Y перпендикулярны друг другу
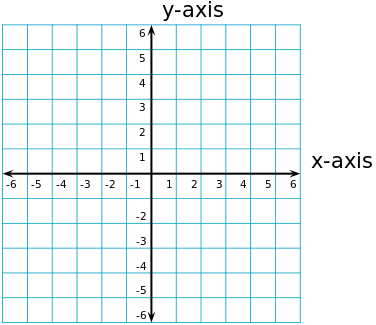
Уравнение окружности
Теперь поговорим об уравнении, которое представляет все точки данной окружности. Действительно, для окружности радиуса \(r\) следующее уравнение описывает точки \((x, y)\), лежащие на окружности:
\[\Large x^2 + y^2 = r^2\]Вышесказанное соответствует уравнению окружности радиуса \(r\), центр которой расположен в точке \((0,0)\), начало координатных осей.
Если радиус равен \(r = 1\), то мы имеем то, что называется единичная окружность .
При рассмотрении приведенного выше уравнения геометрическая интерпретация заключается в том, что \(x\) и \(y\) - стороны треугольника, а \(r\) - его гипотенуза
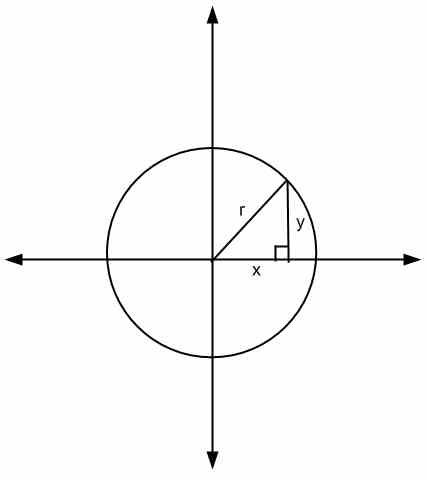
Другой способ увидеть уравнение окружности - это взять квадратный корень с обеих сторон уравнения, таким образом, мы получим \(\sqrt{x^2+y^2} = r\), что указывает на то, что для любой точки \((x,y)\) на окружности, .. расстояние до начала координат (в данном случае центр круга) равен \(r\).
Уравнение окружности, не центрированной в начале координат
Одно из преимуществ работы с координатными осями заключается в том, что точки на окружности и центр могут быть локализовано на осях, и может быть представлена уравнением, как показано выше. Но в общем случае центр окружности не обязательно должен быть началом координат, это может быть любая точка \((x_0, y_0\) на координатных осях, в этом случае уравнение окружности становится:
\[\Large (x-x_0)^2 + (y-y_0)^2 = r^2\]который известен как Общее уравнение окружности . Например, скажем, вам нужно вычислить уравнение окружности радиуса \(r = 4\) с центром в точке \((1,2)\). Итак, в этом случае у нас есть \(x_0 = 1\), \(y_0 = 2\) и \(r = 4\), и тогда мы просто подставляем эти числа в вышеприведенное уравнение и получаем
\[\large (x-1)^2 + (y-2)^2 = 4^2\]или мы можем также написать
\[\large (x-1)^2 + (y-2)^2 = 16\]Пример 1
Напишите уравнение окружности радиуса 3 с центром в начале координат. Используя уравнение, определите, принадлежит ли точка (1, 2) окружности.
Отвечать:
Сначала определим уравнение окружности. В данном случае окружность центрирована в начале координат, поэтому \((x_0, y_0) = (0, 0)\). Следовательно, уравнение имеет вид
\[\large x^2 + y^2 = 3^2\]что совпадает с
\[\large x^2 + y^2 = 9\]Теперь вопрос в том, лежит ли точка (1, 2) на окружности. Мы знаем, что точки на окружности будут такими, что \(x^2 + y^2 = 9\).
Для точки \((1, 2)\) получаем, что \(x = 1\) и \(y=2\), тогда для данного случая этой точки, \(x^2 + y^2 = 1^2 + 2^2 = 1+ 4 = 5\) отлична от 9, а значит \((1,2)\) не принадлежит окружности.
Подробнее об уравнении окружности
Окружность - настолько важная математическая сущность, что о ней написаны целые тома книг. Окружности пересекают геометрию, тригонометрию и алгебру, поэтому в математике они встречаются повсеместно.
Как вычислить уравнение окружности?
Когда мы работаем с окружностью, необходимо решить несколько задач. Прежде всего, необходимо построить уравнение окружности. Например, рассмотрим окружность радиуса \(r = 3\) с центром в точке \((1,1)\).
Исходя из общего уравнения окружности, уравнение имеет вид
\[\large (x-1)^2 + (y-1)^2 = 3^2\]Приведенное выше уравнение можно использовать, например, для определения того, принадлежит ли точка окружности или нет. Что еще можно сделать, чтобы получить уравнение окружности? Потенциально можно расширить квадраты, тогда мы получим
\[\large x^2 - 2x + 1 + y^2 -2y + 1 = 9\]который можно упростить до
\[\large x^2 - 2x + y^2 -2y = 7\]Итак, оба уравнения эквивалентны, в том смысле, что они определяют одну и ту же окружность. Какое из них вам больше нравится? \((x-1)^2 + (y-1)^2 = 3^2\) или \(x^2 - 2x + y^2 -2y = 7\)? Это дело вкуса и того, для чего вы будете использовать формулу.
Площадь круга
Интересно, что для того, чтобы вычислить площадь круга вам не нужно полное уравнение, достаточно знать радиус. Другими словами площадь и окружность круга не зависят от его центра.
Является ли уравнение окружности функцией?
Этот вопрос возникает у многих студентов, и мы должны его разъяснить. Прежде всего, в уравнение окружности это уравнение, а не отношение или функция.
Итак, уравнение окружности определяет отношение, а не функция когда вы алгебраически решить для y в терминах x . Действительно, если мы решим для \(y\), то получим:
\[\large x^2 + y^2 = 9 \Rightarrow y^2 = 9 - x^2 \] \[\large \Rightarrow y = \pm \sqrt{ 9 - x^2} \]Это означает, что для данного \(x\) существуют два связанных значения \(y\), которыми являются \(\sqrt{ 9 - x^2}\) и \(-\sqrt{ 9 - x^2}\), что указывает на то, что уравнение окружности определяет отношение, а не функцию.
Одним из конкретных случаев круга является единичная окружность с уравнением \(x^2 + y^2 = 1\), которое центрировано в начале координат. Единичный круг особенно удобен для работы с тригонометрические выражения в очень наглядной форме.
