Эллипс - это геометрическое место очков в координатных осях, которые имеют свойство, что сумма расстояний данной точки эллипса до двух фиксированных точек (очагов) равна постоянной, которую мы называем \(2a\).

Концепция "геометрического места" очень привлекательна с концептуальной точки зрения, но она может не дать вам четкий вид на то, что вы пытаетесь изобразить.

Попробуйте выполнить упражнение посмотреть уравнение ниже и посмотреть, сможете выяснить, что он выглядит графически;

Не могли бы вы выяснить, как график, просто глядя на уравнение выше.Я так и думал.Позвольте мне представить эллипс для вас:

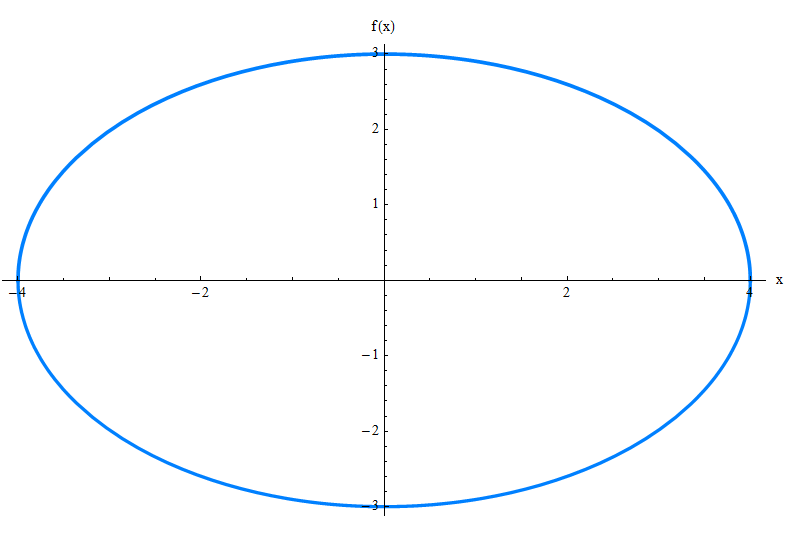
Общее уравнение эллипса

Без особой теоретической дискуссии мы укажем, что общее уравнение эллипса с центром по происхождению, а с очагами на оси x, для \(a \ge b\)

Для эллипса, описанного выше, он имеет очаги в точках \((-c, 0)\) и \((c, 0)\), где \(c = \sqrt{a^2 - b^2}\).

Теперь, что происходит с уравнением вышеуказанной гиперболы, когда \(b > a\)?

В этой компенсировании начаги находятся на оси у y, и \((0, c)\), где \(c = \sqrt{b^2 - a^2}\).

Теперь, ...

Все, что вам нужно сделяться в этой слайчае, замените \(x\) \(y\) _\(x-h\).

Следовательно, Делая перевод, Мы получим это Уравнение общего Эллипса

Вышеузазнанный эллипс Есть центр __xxyz_a__, и у нее есть очаги __xxy__, где \(c = \sqrt{a^2 - b^2}\), где \(c = \sqrt{a^2 - b^2}\)_d__ ___x_f_e__, где \(c = \sqrt{b^2 - a^2}\) для \(b>a\).

Пример 1.

НАЙТИ ОЧАГИ, ЭЛЛИПСА:

Отвечать:

Прежде всего,основываясь на структуре уравнения выше,эллипс центрирован при происхождении\((0, 0)\)Обратите внимание,что основной полу оси-.4,что связано с__xxyz_b__,поэтому тогда фокусы на осиY.

ИЗ УРАВНЕНИЯ МЫ ПОЛУЧЛИ, ЧТО \(a^2 = 9\) I \(b^2 = 16\). Мы находим, что \(c = \sqrt{b^2 - a^2} = \sqrt{16 - 9} = \sqrt 7\). Поэ тому очаги находят в \((0, -\sqrt{7})\) и \((0, \sqrt{7})\).

Пример 2.

Найдите Уравнение Эллипса, Содержатоточного в \((0, 2)\) с одного фокусом на \((6, 2)\)

Отвечать:

.

Следовательно, Уравнение Эллипса:

Эллипс и общие конические разделы

Как и в случае с корпусом парабола,гипербола и круг,эллипс плотно связанно с конусом.Древнегреческим математиком по имени Аполлония обнаружил эту связь,с тем,что называется СЕЦЦИИ КОНИЧЕСКИХ Отказ

Коническая секция соответствует формам,которые образуются,когда вы делаете разрез через конус с плоскостью,а в зависимости от относительного угла конуса и плоскости формы поперечного сечения изменяется.

Действительно,в зависимости от угла конуса и плоскости лица друга друга,форма поперечного сечения может представлять собой параболу,круг,эллипс или гипербол.Это изображены на графике ниже: