Гипербол является геометрическим местом точек в координатных осях, которые имеют свойство, что разница между расстояниями до двух фиксированных точек (очагов), равна постоянной, которую мы называем \(2a\).

Естественно, это звучит немного запугивающим и слишком техническим, но действительно, как определяется гипербол.

Может быть, если я дам вам уравнение гиперболы, вы бы "узнали" это.

Давайте попробуем: это уравнение очень общей гиперболы:

Не могли бы вы выяснить, как это выглядит, просто проверяя его уравнение?Возможно нет.Поэтому я представляю гиперболу, графически для вас:

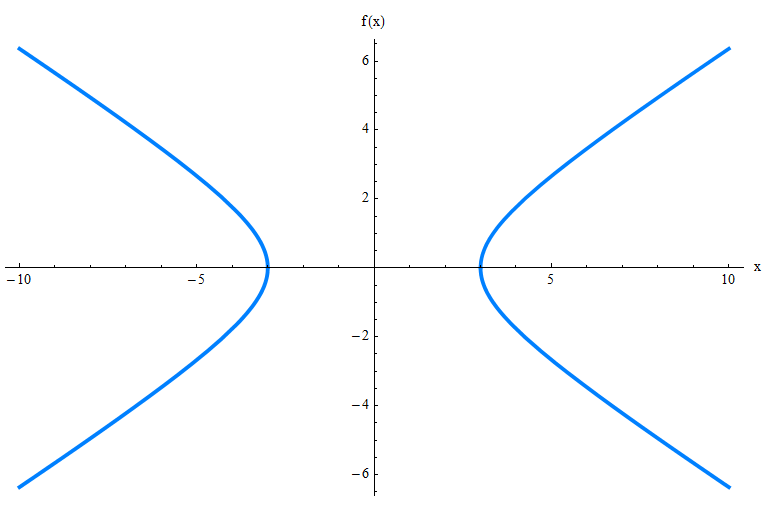
Вышеуказанный график показывает только график гиперболы, но есть много других элементов, которые вам нужно знать, такие как уклон асимптота, вершины и очаги.Проверьте график ниже.

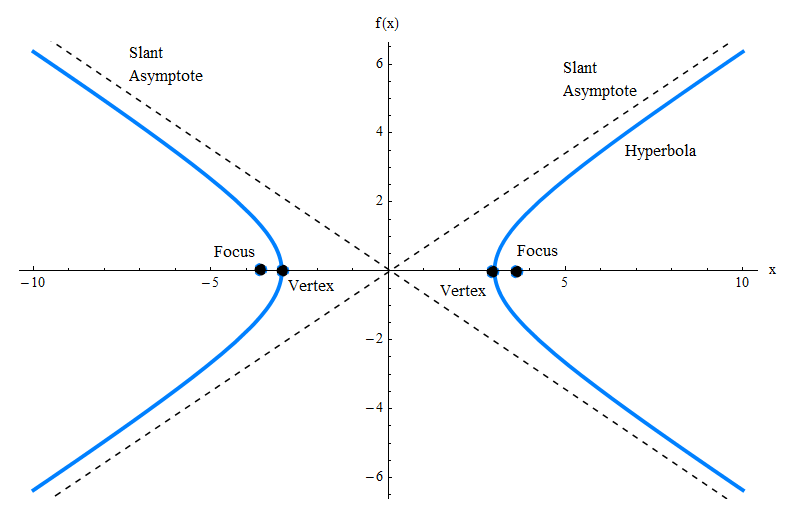
Общее уравнение гиперболы

Без особой теоретической дискуссии мы заявляем, что общее уравнение гиперболы с очагами на оси X

Для гиперболы, описываемой вышеуказанным уравнением, у него есть вершины в точках \((-a, 0)\) и \((a, 0)\), и у него есть очаги на точках \((-c, 0)\) и \((c, 0)\), где \(c = \sqrt{a^2 + b^2}\).

Интересная особенность этой гиперболы в том, что у него есть два асимптота

Асимпте 1. : \(\displaystyle y = \frac{b}{a}x\)

Асимпте 2. : \(\displaystyle y = -\frac{b}{a}x\)

Теперь, что происходит с уравнением гиперболы, если вместо вершины переведены данной точкой \((k,h)\)?

Все, что вам нужно сделать в этом случае, замените \(x\) \(x-k\) и заменить \(y\) _\(x-h\).

Следовательно, делая перевод, мы получаем, что уравнение общей гиперболы

Приведенная выше гипербола имеет вершины в точках \((k-a, h)\) и \((k+a, h)\), и у него есть очаги в точках \((k-c, h)\) и \((k+c, h)\), где \(c = \sqrt{a^2 + b^2}\).

Уравнения уклона асимптота \(y = \frac{b}{a}(x-k) + h\) и \(y = -\frac{b}{a}(x-k) + h\).

Что происходит с гиперболами, которые открываются вдоль оси Y?

По симметрии все, что нам нужно сделать, это просто заменить роли \(x\) и \(y\) в общем уравнении гиперболы, у нас уже есть.В практичности это означает, что везде, где \(x\) появляется в уравнении парабола, мы меня изменим \(y\) и наоборот для \(y\).

Итак, в случае гиперболы, который открывает длинную ось X, общее уравнение

Приведенная выше гипербола имеет вершины в точках \((k, h - b)\) и \((k, h+b\), и у него есть очаги в точках \((k, h-c)\) и \((k, h+c)\), где \(c = \sqrt{a^2 + b^2}\).

Уравнения уклона асимптота \(y = \frac{b}{a}(x-k) + h\) и \(y = -\frac{b}{a}(x-k) + h\).

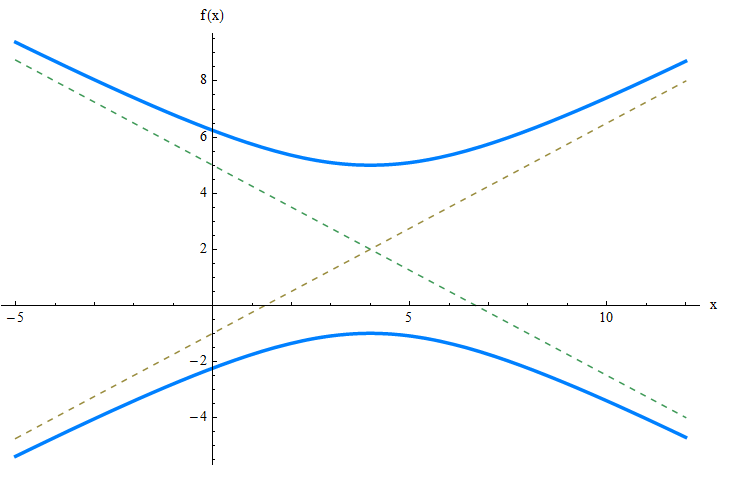
Пример 1.

Найти очаги, вершины и уклон асимптотам гиперболы:

ОТВЕЧАТЬ:

Эта гипербола открывается вдоль оси Y.В этом случае значения перевода \(k = 4\) и \(h = 2\).Кроме того, мы получаем это \(a = \sqrt{16} = 4\) и \(b = \sqrt{9} = 3\).Следовательно, мы получаем это \(c = \sqrt{a^2+b^2} = \sqrt{4^2+3^2} = \sqrt{25} = 5\).

Следовательно, очаги \((k, h-c) = (4, 2 - 5) = (4, -3)\) и \((k, h+c) = (4, 2 + 5) = (4, 7)\).

Вершины \((k, h-b) = (4, 2 - 3) = (4, -1)\) и \((k, h+b) = (4, 2 + 3) = (4, 5)\).

Слантические асимптоты

Графически:

Пример 2.

Найдите уравнение гиперболы с очагами на \((-4, 0)\) и \((4, 0)\) vertex, фокусируйтесь на \((6, 0\).

ОТВЕЧАТЬ:

Обратите внимание, что очаги и вершины находятся на оси x, поэтому гипербола открывается вдоль оси x.Кроме того, поскольку очаги симметричны относительно происхождения, а одна вершина \((4, 0)\), мы получаем это \(a = 4\).И поскольку один фокус находится в \((6, 0)\), мы получаем это \(b = \sqrt{6^2 - 4^2} = \sqrt{20} = 2\sqrt 5\).

Следовательно, уравнение гиперболы:

Гипербола и общие конические разделы

Как и в случае с корпусом парабола, гипербола плотно связана с конусом.Действительно, греческие математики по имени Аполлония, является тем, кто обнаружил эту связь, понимая концепцию конических разделов.

Коническая секция возникает, когда вы делаете разрез конуса с плоскостью и в зависимости от относительного угла конуса и плоскости в точке среза, конус разрезается таким образом, когда поперечное сечение имеет определенную формуОтказ

Таким образом, в зависимости от относительного угла среза у нас есть разные формы сечения, и это парабола, круг, эллипс и гипербола.Смотрите график ниже: