More about the Law Of Sines

This calculator will allow you to solve a triangle by using the Law of Sines in at least part of the steps. There are different settings in which it will pop up when solving triangles, but one of the most clear situations to use it is when you know two angles and the opposite side of the triangle.

Understanding the Law of Sines Formula

The Law of Sines formula is expressed as:

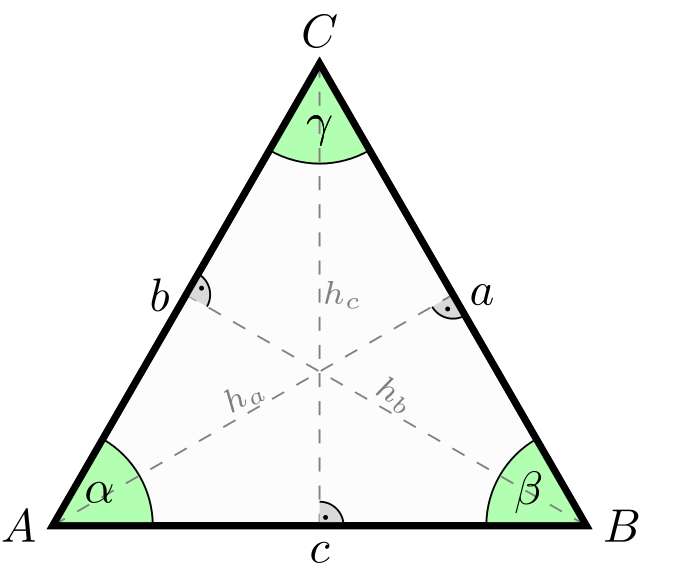
\[\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2R\]

where in this case we have that \(a\), \(b\), and \(c\) are the lengths of the sides of a triangle, \(A\), \(B\), and \(C\) are the opposite angles, and \(R\) is the radius of the circumscribed circle around the triangle.

Often times the law of sines is imply written as

\[\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}\]

which is typically sufficient to solve a triangle.

When to Use the Law of Sines?

The Law of Sines is particularly useful when:

• You know two angles and one side of a triangle (AAS or ASA).
• You need to find the remaining sides or angles in such cases.

Step-by-Step Guide to Using the Law of Sines Calculator

How to Use a Law of Sines Calculator

Here are the steps to use a Law of Sines calculator effectively:

• Assess what information you have available and then enter the known values of angles and sides into the calculator.
• Then, the unknown value that you need to calculate is the one targeted.
• Pressing calculate gives you the result and the steps of the process.

Examples of Law of Sines in Action

Let's look at an example:

Given triangle ABC with \(A = 45^\circ\), \(B = 60^\circ\), and \(a = 10\) cm, find side \(b\):

\[\frac{a}{\sin A} = \frac{b}{\sin B}\] \[\frac{10}{\sin 45^\circ} = \frac{b}{\sin 60^\circ}\] \[b = \frac{10 \times \sin 60^\circ}{\sin 45^\circ} \approx 12.25 \text{ cm}\]

Common Problems and Solutions with the Law of Sines

Here are some common issues and how to address them:

• Ambiguous Case: When you have two sides and an angle opposite one of them, there might be two possible solutions or none at all.
• Zero or Negative Sine: If \(\sin A = 0\), then \(A = 0^\circ\) or \(180^\circ\), which means the triangle might not exist or be degenerate.

How to Solve Triangles Using the Law of Sines

Follow these steps to solve a triangle:

• First, identify the known angles and sides. Typically you will need 3 pieces of information to fully determine the triangle
• Use the Law of Sines to find the unknown sides or angles, when two angles are known.
• Check for the ambiguous case if applicable.

The Ambiguous Case in the Law of Sines

The ambiguous case arises when:

• You have two sides and an angle opposite one of them.
• There can be zero, one, or two solutions depending on the given values.

Proof of the Law of Sines

The Law of Sines can be derived from the following:

• Consider a triangle inscribed in a circle.
• Use the fact that the angle subtended by an arc at the center is twice the angle at any point on the circumference.
• Apply trigonometric identities to relate the sides and angles.

Relationship Between Law of Sines and Law of Cosines

While the Law of Sines relates the sides to the sines of their opposite angles, the Law of Cosines provides a relationship involving the cosine of one angle:

\[c^2 = a^2 + b^2 - 2ab \cos C\]

This formula is useful when you know all three sides or two sides and the included angle.

Advanced Applications: Spherical and Hyperbolic Law of Sines

In spherical geometry:

• The Law of Sines becomes \(\frac{\sin a}{\sin A} = \frac{\sin b}{\sin B} = \frac{\sin c}{\sin C}\).
• For hyperbolic geometry, the formula adjusts to account for the curvature of space.

Higher Dimensional Law of Sines

In higher dimensions, the Law of Sines extends to:

• Polytopes where the sine of angles between hyperplanes is considered.
• It involves more complex trigonometric identities and geometric considerations.

Why Does the Law of Sines Work?

The Law of Sines is intrinsically woven in core fabric of the principles of Geometry and Triangles, and it works because:

• It is derived from the properties of circles and the relationship between angles and arcs.
• It reflects the symmetry and proportionality inherent in triangles.

Naturally, the Law of Sines can be proven formally, but its proof is beyond the scope of the tutorial.

FAQ: Law of Sines for beginners

What is the Law of Sines?

The Law of Sines is a trigonometric principle that relates the sides of a triangle to the sines of its angles.

When should you use the Law of Sines?

Use the Law of Sines when you know two angles and one side or when you need to find an angle or side in such a scenario.

Can the Law of Sines be used for any triangle?

Yes, but it's most straightforward for non-right triangles. For right triangles, the Pythagorean theorem might be simpler.

What is the ambiguous case?

The ambiguous case occurs when there are two possible triangles or none at all, given two sides and an angle opposite one of them.

How does the Law of Sines relate to the Law of Cosines?

Both laws help solve triangles, but the Law of Sines deals with angles and opposite sides, while the Law of Cosines involves sides and the cosine of an included angle.

Explore More Trigonometric Calculators

If you're delving into the world of trigonometry, understanding the Law of Sines is just the beginning. You might find it beneficial to explore the Law of Cosines, which complements the Law of Sines by providing another method to solve triangles when you have different sets of known information. For those interested in the fundamental trigonometric functions, our Sin Calculator can help you compute the sine of any angle, which is crucial for many applications in physics, engineering, and beyond.

Furthermore, if your studies or work involve more complex trigonometric identities, you might appreciate the Double Angle Formula calculator. This tool can simplify calculations involving angles that are twice as large, which often appear in calculus and advanced trigonometry problems. Each of these calculators offers unique insights and tools to enhance your understanding and application of trigonometry in various scenarios.