More about this Area and Volume of a Pyramid Calculator

This calculator deals with square pyramids (those pyramids with squared base), for which you need to provided the side $l$ of the base and the corresponding height $h$. A square pyramid looks like:

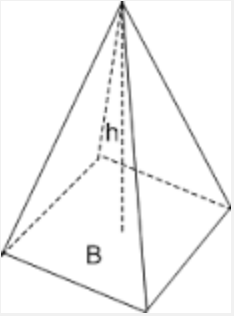
How to Compute the Area and Volume of a Pyramid?

In order to compute the surface area and volume of square pyramid with side $l$ and height $h$ we use the following formulas:

$$\text{Area} = l^2 + 2l\sqrt{\frac{l^2}{4} + h^2}$$ $$\text{Volume} = \frac{l^2 h}{3}$$

Computationally speaking, it is quite simple to compute the surface area and the volume of a square pyramid, by simply plugging the side $l$ and height $h$ in the above formulas. For example, if the side is $l = 3$ and the height is $h = 4$, we compute

$$\text{Area} = l^2 + 2l\sqrt{\frac{l^2}{4} + h^2} = 3^2 + 2\cdot 3\sqrt{\frac{3^2}{4} + 4^2} = 34.632$$ $$\text{Volume} = \frac{l^2 h}{3} = \frac{3^2\cdot 4}{3} = 12$$

which completes the calculation.

Other geometric calculators

Our site provides a number of geometric calculators, including this sphere area and volume calculator , among many others.