抛物线
Parabola是坐标轴中的几何点,其具有与固定点（称为焦点）和线（称为directix）等距的属性。
我知道听起来有什么看法,但我们会经历它,最后你会看到它并不那么难。
所以,如果我告诉那个
功能\(f(x) = x^2\)代表代表物线？
确定它会有所帮助。而且你可能会想到“为什么你没有告诉我从一开始就是抛物线是那种功能？”。
因为没有抛物线,有一个无限数量的。抛物线甚至不必由函数表示。是的,一些关系是抛物线,我们会看到。
有一件事要提及：使用函数和关系,有抛物线沿 \(y\) 轴“打开”,并且沿 \(x\) 轴“打开”的抛物线。
最后,通过对称性,很容易意识到那些沿着y轴“打开”的抛物线具有与沿x轴“打开”的结构相同,因此可以学习如何处理一种类型。
抛物线的一般方程
基于Directrix的位置和焦点,有简单的推导来获取抛物线的等式,但我们将跳过此介绍中的推导。
检查下图。我们需要识别抛物线的一些重要元素：我们有顶点,焦点和鬼焦。
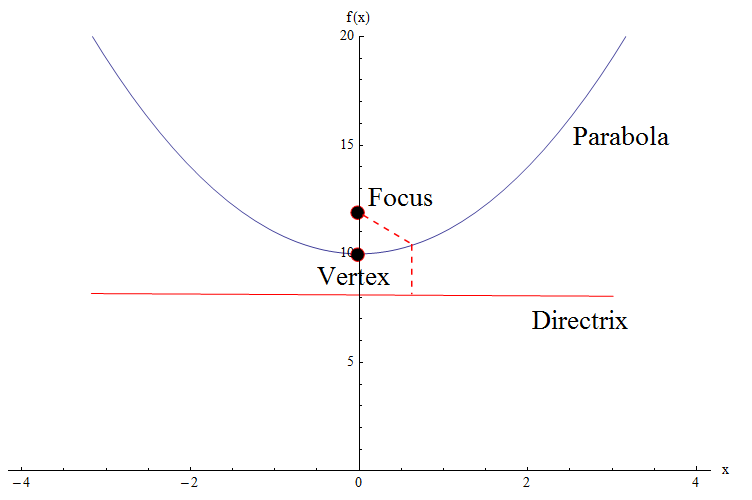
我们不会详细介绍,但我们会说具有顶点的一般抛物线的等式,具有焦点\((0, a)\)和directrix等于\(y = -a\)
这个抛物线是沿着y轴打开的抛物线。
现在,在给定点\((k,h)\) 时,我们希望在原点上遇到顶点时会发生什么
那么,这是使用坐标系的魔力,所有我们需要通过点点\((k,h)\)进行翻译？但是你如何通过\((k,h)\)来翻译？
简单的！无论您有\(x\),您将通过\(x-k\)替换它,无论\(y\),您都会通过\(x-h\)替换它。
因此,在\((k,h)\) _和direcrix等于\(y = h-a\)的焦点\((k, h+a)\)和direcrix等于\(y = h-a\)的常规抛物线的一般抛物线的等式
\[\large y-h = 4a(x-k)^2\]哪个可以写成
\[\large \boxed{ y = 4a(x-k)^2 + h }\]沿x轴打开的抛物线会发生什么？
通过对称性,简单地通过替换\(x\)和\(y\)在我们已经拥有的抛物线的等式中的角色来获得。实际上,这意味着无论\(x\)出现在我们所拥有的抛物线的等式中,我们会更改\(y\),反之亦然\(y\)。
因此,具有顶点的普通抛物线的方程在点\((h,k)\)中,焦点\((h+a, k)\)和direcrix等于\(x = h-a\)是：
\[\large \boxed{ x = 4a(y-k)^2 + h }\]注意差异：
当抛物线具有表单\(y = -a\)的directrix时,抛物线沿着y轴打开（取决于焦点是否在dircrix上方或下方）。
当抛物线具有表单\(x = -a\)的directrix时,抛物线沿x轴打开（左或向右,根据焦点是指侧的左侧或右侧）。
例1
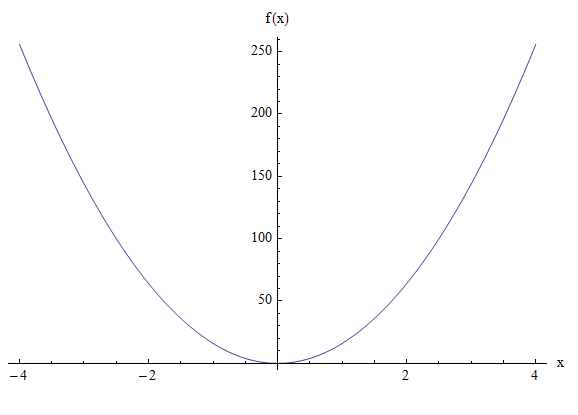
找到具有directrix _ xyz _ a _和焦点_ xyz_b _的抛物线的等式。也找到顶点。
回答：
顶点是抛物线上的,所以它与directrix \(y = -4\)等距离,焦点\((0, 4)\),所以顶点是\(0, 0)\)。另一方面,对于在原点的顶点的抛物线上,Directrix的等式是\(y = -a\),因此在这种情况下\(a = 4\)。因此,抛物线的等式是
\[ \large y = 4ax^2 = 4(4)x^2 = 16x^2 \]图形方式：
例2.
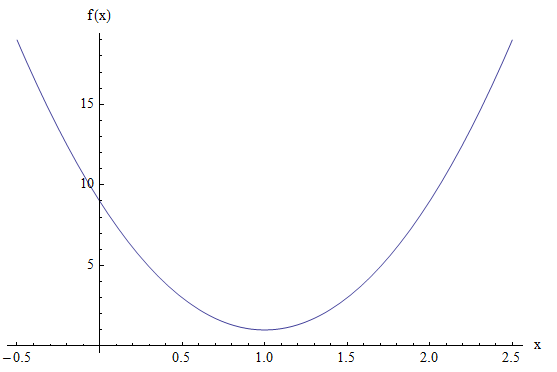
找到抛物线的顶点,焦点和directrix \(y = 8x^2 - 16x + 9\)。
回答：
首先,我们需要完成广场：
\[\large y = 8x^2 - 16x + 9 = 8(x^2 - 2x) + 9 \] \[\large = 8(x^2 - 2x + 1 - 1) + 9 \] \[\large = 8(x^2 - 2x + 1) + 9 - 8 \] \[\large = 8(x-1)^2 + 1 \]与一般方程等同于这一点,我们发现顶点是\((1, 1)\)的点,而且我们还有那个\(4a = 8\),所以\(a = 2\),因此,directrix是\(y = h - a = 1 - 2 = -1\),焦点是\((k, h + a) = (1, 1+2) = (1, 3)\)。
图形方式：
抛物线和一般圆锥部分
像它一样奇怪,抛物线与锥体紧密相关。你怎么样？一个名叫Apollonius的希腊数学家是使用圆锥形截面的现代版本的贡献来贡献。
Apollonius和其他数学家发现,当您用平面切割锥形时,根据锥体和平面的相对角度,锥体被切割,使得该部分具有不同的形状。
这些部分的不同形状,取决于切割的相对角度是我们所知道的抛物线,圈,椭圆和双曲线,如下图所示：
关于抛物线的更多信息
沿Y轴打开的一般抛物线,原点\((0, 0)\)处具有顶点\((0, 0)\)的顶点具有以下功能表示\(y = 4ax^2\)。
然后,通过对称性,沿x轴打开的一般抛物线,顶点\((0, 0)\)处具有以下功能表示\(x = 4ay^2\)。
然后,可以通过将翻译应用于给定点\((k, h)\)来获得一般顶点。
应用程序
Parabola在物理学中具有无数应用程序,因为重力力和牛顿的法律运作的方式,大多数抛出的机构的轨迹将遵循抛物线轨迹。
此外,代数说话,抛物线一直出现在代数中,因为所有二次函数都有抛物线图,并且二次函数在代数中出现很多。
此外,在找到最小值和最大值时,抛物线出现在微积分中。事实证明,许多最大化和最小化问题具有二次函数来最大化和几何上,最大值或最小值（取决于抛物线,如果抛物线打开或向上）是在顶点实现的。