双曲线是坐标轴中的点的几何点,其具有与两个固定点（焦点）之间的差值之间的差异等于常数,这是我们以\(2a\)为常数。

当然,这听起来有点令人生畏和过于技术性,但实际上是一种定义双曲线的方式。

也许,如果我给你一个双曲线的等式,你会“识别”它。

让我们尝试：这是一个非常通用的双曲线的等式：

你能弄清楚它如何看待它的等式？可能不是。所以我介绍了双曲线,以图形为您：

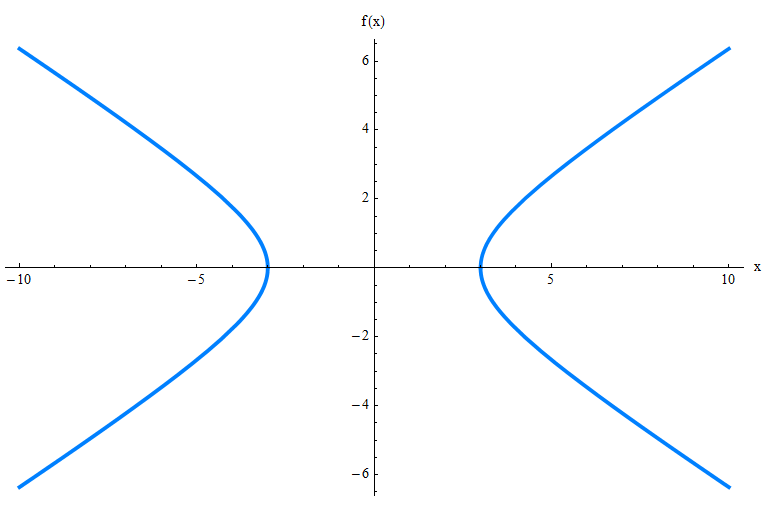
上图仅显示了双曲线图,但您需要了解许多其他元素,例如倾斜渐近,顶点和焦点。检查下图。

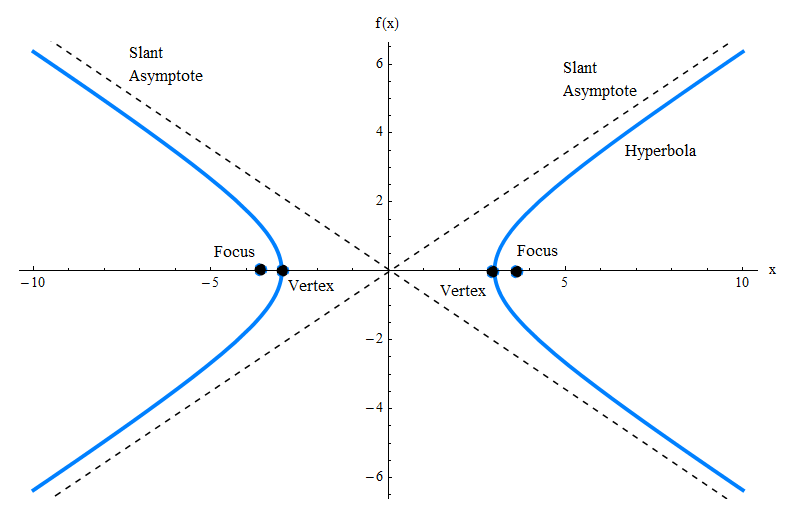
双曲线的一般方程

在没有大部分理论讨论中,我们将说明X轴上用焦点的双曲线的一般方程是

对于由上述等式描述的双曲线,它在点\((-a, 0)\)和\((a, 0)\)处具有顶点,并且它在点\((-c, 0)\)和\((c, 0)\)处具有焦点,其中\(c = \sqrt{a^2 + b^2}\)。

这种双曲线的一个有趣的特征是它有两个倾斜的渐近斑点

渐近1 ：\(\displaystyle y = \frac{b}{a}x\)

渐近2 ：\(\displaystyle y = -\frac{b}{a}x\)

现在,在双曲线的等式中发生了什么,如果翻页是由给定点\((k,h)\)翻译的？

在这种情况下,您必须做的就是用\(x-k\)替换\(x\),并通过\(x-h\)替换\(y\)。

因此,通过进行翻译,我们得到了一般双曲线的等式

上面的双曲线在点\((k-a, h)\)和\((k+a, h)\)处具有顶点,并且它在点\((k-c, h)\)和\((k+c, h)\)中有焦点,其中\(c = \sqrt{a^2 + b^2}\)。

倾斜渐近的等式是\(y = \frac{b}{a}(x-k) + h\)和\(y = -\frac{b}{a}(x-k) + h\)。

与y轴打开的双曲线会发生什么？

通过对称性,我们要做的就是简单地替换\(x\)和\(y\)在我们已经拥有的双曲线的一般方程中的角色。实际上,这意味着无论\(x\)出现在我们所拥有的抛物线的等式中,我们会更改\(y\),反之亦然\(y\)。

所以,在X轴长长的双曲线的情况下,通用等式是

上面的双曲线在点\((k, h - b)\)和\((k, h+b\)处具有顶点,并且它在点\((k, h-c)\)和\((k, h+c)\)中有焦点,其中\(c = \sqrt{a^2 + b^2}\)。

倾斜渐近的等式是\(y = \frac{b}{a}(x-k) + h\)和\(y = -\frac{b}{a}(x-k) + h\)。

例1

找到双曲线的焦点,顶点和倾斜渐近渐近渐变：

回答：

这种双曲线沿Y轴打开。在这种情况下,翻译值是\(k = 4\)和\(h = 2\)。此外,我们得到\(a = \sqrt{16} = 4\)和\(b = \sqrt{9} = 3\)。因此,我们得到了\(c = \sqrt{a^2+b^2} = \sqrt{4^2+3^2} = \sqrt{25} = 5\)。

因此,焦点是\((k, h-c) = (4, 2 - 5) = (4, -3)\)和\((k, h+c) = (4, 2 + 5) = (4, 7)\)。

顶点是\((k, h-b) = (4, 2 - 3) = (4, -1)\)和\((k, h+b) = (4, 2 + 3) = (4, 5)\)。

倾斜的渐近斑点是

图形方式：

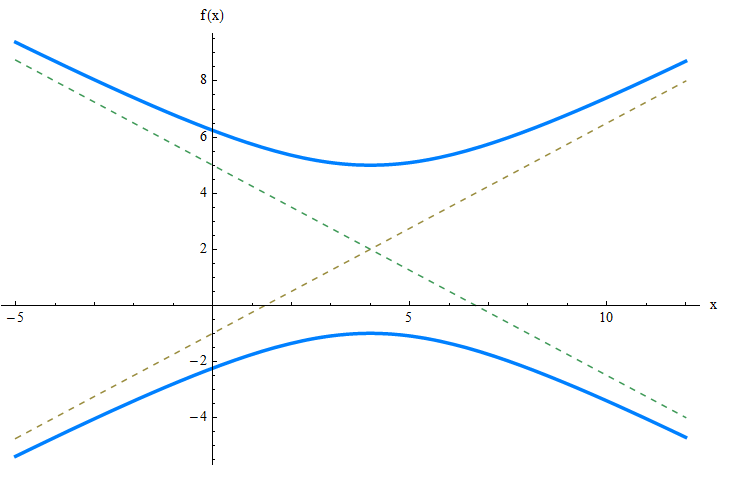
例2.

在\((-4, 0)\)和\((4, 0)\)顶点上找到双曲线的等式,od\((4, 0)\)顶点,焦点\((6, 0\)。

回答：

请注意,焦点和顶点位于x轴上,因此双曲线沿x轴打开。此外,由于焦点相对于原点对称,因此一个顶点是\((4, 0)\),因此我们得到\(a = 4\)。由于一个焦点在\((6, 0)\),我们得到了\(b = \sqrt{6^2 - 4^2} = \sqrt{20} = 2\sqrt 5\)。

因此,双曲线的等式是：

双曲线和一般圆锥部分

与抛物线的情况相同,双曲线与锥体紧密相关。事实上,一个名叫阿波罗尼乌斯的希腊数学家是通过了解圆锥部分的概念来发现这一联系的人。

当用平面切割锥体时,并且根据锥体的相对角度和切割点的平面的相对角度,锥体被切割,锥体被切割,其中横截面具有特定形状。

因此,取决于切割的相对角度,我们具有不同形状的部分,这些是抛物线,圆形,椭圆和双曲线。请参阅下图：