The Hyperbola
A hyperbola is the geometric place of points in the coordinate axes that have the property that the difference between the distances to two fixed points (the foci), is equal to a constant, which we denominate \(2a\).
Naturally, that sounds a bit intimidating and too technical, but it is indeed the way that a hyperbola is defined.
![]() Maybe, if I give you the equation of a hyperbola, you would "recognize" it.
Maybe, if I give you the equation of a hyperbola, you would "recognize" it.
![]() Let us try: this is the equation of a very general hyperbola:
Let us try: this is the equation of a very general hyperbola:
Could you figure out how it looks by just checking its equation? Probably not. So I introduce the hyperbola, graphically for you:
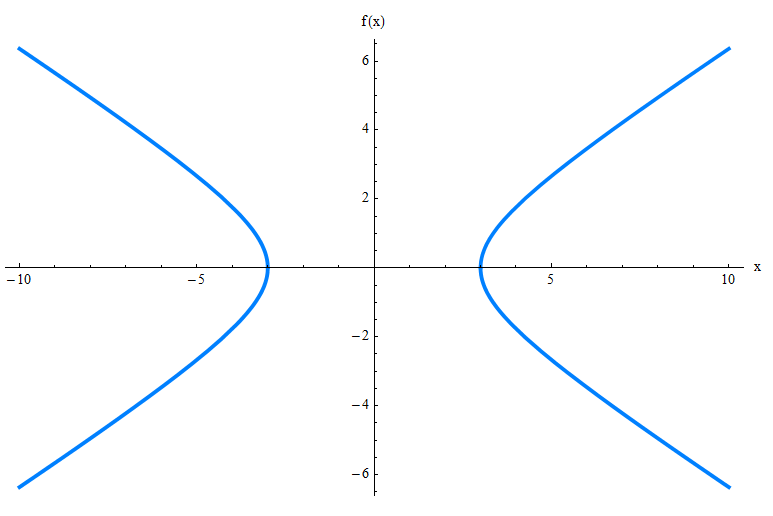
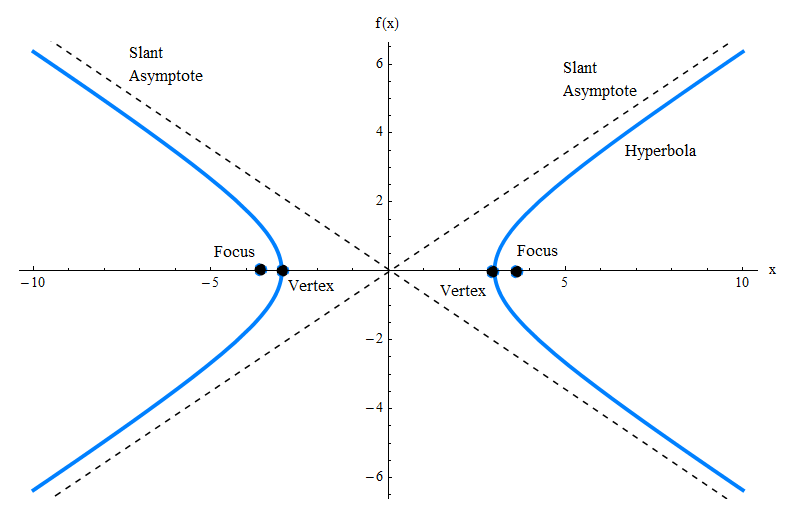
The above graph shows you only the graph of the hyperbola, but there are many other elements you need to be aware of, such as the slant asymptotes, the vertices and foci. Check the graph below.
The General Equation of the Hyperbola
Without much of a theoretical discussion, we will state that the general equation of the hyperbola with foci on the x-axis is
\[\large \displaystyle \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 \]
![]() For the hyperbola described by the above equation, it has vertices at points \((-a, 0)\) and \((a, 0)\) and it has foci at points \((-c, 0)\) and \((c, 0)\), where \(c = \sqrt{a^2 + b^2}\).
For the hyperbola described by the above equation, it has vertices at points \((-a, 0)\) and \((a, 0)\) and it has foci at points \((-c, 0)\) and \((c, 0)\), where \(c = \sqrt{a^2 + b^2}\).
An interesting feature of this hyperbola is that it has two slant asymptotes
![]() Asymptote 1
: \(\displaystyle y = \frac{b}{a}x\)
Asymptote 1
: \(\displaystyle y = \frac{b}{a}x\)
![]() Asymptote 2
: \(\displaystyle y = -\frac{b}{a}x\)
Asymptote 2
: \(\displaystyle y = -\frac{b}{a}x\)
Now what happens with the equation of the hyperbola, if instead the vertices are translated by a given point \((k,h)\)?
All you have to do in that case is replace \(x\) by \(x-k\), and replace \(y\) by \(x-h\).
Hence, by doing a translation, we get that the equation of a general hyperbola is
\[\large \boxed{\displaystyle \frac{(x-k)^2}{a^2} - \frac{(y-h)^2}{b^2} = 1 }\]The above hyperbola has vertices at points \((k-a, h)\) and \((k+a, h)\) and it has foci at points \((k-c, h)\) and \((k+c, h)\), where \(c = \sqrt{a^2 + b^2}\).
The equations of the slant asymptotes are \(y = \frac{b}{a}(x-k) + h\) and \(y = -\frac{b}{a}(x-k) + h\).
What happens with the hyperbolas that open up along the y-axis?
By symmetry, all we have to do is to simply replace the roles of \(x\) and \(y\) in the general equation of the hyperbola we already have. In practicality, this means that wherever \(x\) appears in the equation of the parabola we have, we change it \(y\), and vice versa for \(y\).
So then, in the case of a hyperbola that opens long the x-axis, the general equation is
\[\large \boxed{\displaystyle \frac{(y-h)^2}{b^2} - \frac{(x-k)^2}{a^2} = 1 }\]The above hyperbola has vertices at points \((k, h - b)\) and \((k, h+b\) and it has foci at points \((k, h-c)\) and \((k, h+c)\), where \(c = \sqrt{a^2 + b^2}\).
The equations of the slant asymptotes are \(y = \frac{b}{a}(x-k) + h\) and \(y = -\frac{b}{a}(x-k) + h\).
EXAMPLE 1
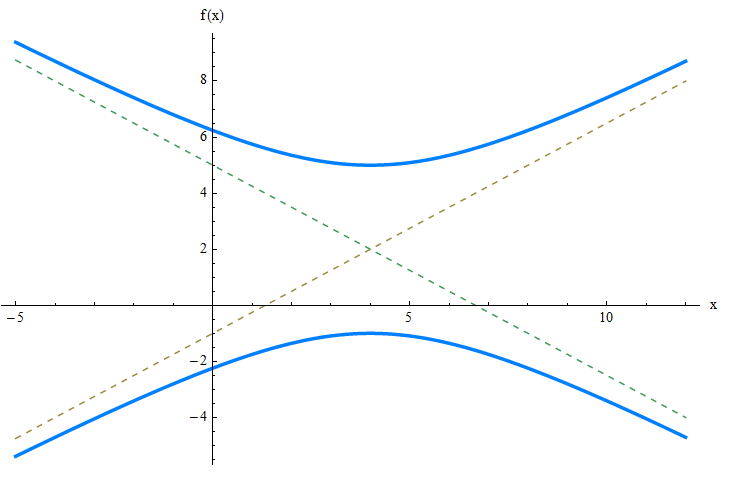
Find the foci, vertices and slant asymptotes of the hyperbola:
\[\large \displaystyle \frac{(y-2)^2}{9} - \frac{(x-4)^2}{16} = 1 \]ANSWER:
This hyperbola opens along the y-axis. In this case, the translation values are \(k = 4\) and \(h = 2\). Also, we get that \(a = \sqrt{16} = 4\) and \(b = \sqrt{9} = 3\). Hence, we get that \(c = \sqrt{a^2+b^2} = \sqrt{4^2+3^2} = \sqrt{25} = 5\).
Hence, the foci are \((k, h-c) = (4, 2 - 5) = (4, -3)\) and \((k, h+c) = (4, 2 + 5) = (4, 7)\).
The vertices are \((k, h-b) = (4, 2 - 3) = (4, -1)\) and \((k, h+b) = (4, 2 + 3) = (4, 5)\).
The slant asymptotes are
\[\displaystyle y = \frac{b}{a}(x-k) + h = \frac{3}{4}(x-4) + 2\] \[\displaystyle y = -\frac{b}{a}(x-k) + h = \frac{3}{4}(x-4) + 2\]Graphically:
EXAMPLE 2
Find the equation of the hyperbola with foci at \((-4, 0)\) and \((4, 0)\) vertex, focus at \((6, 0\).
ANSWER:
Notice that the foci and vertices are on the x-axis, so then the hyperbola opens along the x-axis. Also, since the foci are symmetric with respect to the origin, and one vertex is \((4, 0)\), we get that \(a = 4\). And since one focus is at \((6, 0)\), we get that \(b = \sqrt{6^2 - 4^2} = \sqrt{20} = 2\sqrt 5\).
Therefore, the equation of the hyperbola is:
\[\large \displaystyle \frac{(y-h)^2}{b^2} - \frac{(x-k)^2}{a^2} = 1 \] \[\large \displaystyle \Rightarrow \frac{x^2}{16} - \frac{y^2}{20} = 1 \]The Hyperbola and general Conic Sections
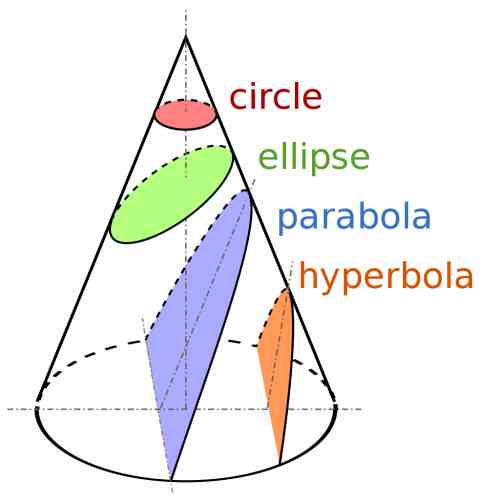
Same as with the case of the parabola, the hyperbola is tightly related to the cone. Indeed a Greek mathematicians named Apollonius is the one who discovered this connection, by understanding the concept of conic sections.
A conic section occurs when you make a cut of a cone with a plane, and depending on the relative angle of the cone and the plane at the point of cut, the cone is cut in a way in which the cross section has a specific shape.
So, depending on the relative angle of cut we have different shapes of the section, and these are the parabola, circle, ellipse, and hyperbola. See the graph below:
More About the Hyperbola
A hyperbola with vertex at the origin, that opens along the x-axis has equation \(\displaystyle \frac{x^2}{a^2} - \frac{y^2}{a^2} = 1 \), whereas a hyperbola, that opens along the y-axis has equation \(\displaystyle \frac{y^2}{a^2} - \frac{x^2}{a^2} = 1 \).
Then, a general vertex can be obtained simply by applying a translation to a given point \((k, h)\).
Applications
The hyperbola has many applications in the practical world, as well as in Astronomy. One difference with the parabola is that the hyperbola has slant asymptotes, which the parabola does not have.
Algebraically speaking, a hyperbola resembles an ellipse much more than it does a parabola, although the difference in sign with the ellipse makes a world of difference in its shape and properties.
Another important type of conic section is the parabola, of which you can learn about in this tutorial . Also, you can also learn all there is to learn about the circle and the ellipse .
