More on this this Scalene Triangle

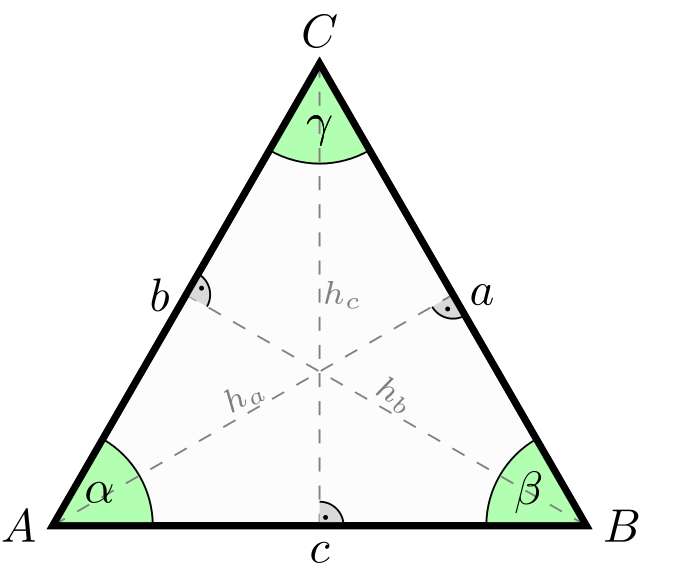
The idea of this triangle calculator is that you have an scalene triangle, which has no special type of symmetry, where potentially all sides are different. Then you will need to feed the calculator with the three sides so then you can find the three corresponding angles.

Once you provide valid numeric expressions for the 3 sides of the triangle, the next step you need to take is to click on the "Calculate" button, and you will get all of the steps of the calculation shown.

What is a Scalene Triangle?

A scalene triangle is a type of triangle where all three sides are of different lengths, and all angles are different. This comes as a consequence of the lack of symmetry found in this type of triangle. Indeed, this unique property sets it apart from other triangles like isosceles or equilateral triangles.

Key Properties of a Scalene Triangle

What defines a scalene triangle? Here are the defining characteristics of a scalene triangle:

• All sides are unequal in length.
• All angles are different.
• It has no lines of symmetry.
• The sum of any two sides is always greater than the third side.

These unique lack of symmetry properties make it often time necessary use the most powerful tools we have available, including the Law of Sines and Law of Cosines.

How to Identify a Scalene Triangle?

Here are the steps you can take to determine if a triangle is scalene:

• Measure the lengths of all three sides.
• Check if all sides are different.
• Verify that all angles are different.

Nothing too hard there, just compare the measurements available. Likely you will have the sides given so use the first criterion.

Scalene Triangle Formulas

Here are some key formulas for scalene triangles:

• Perimeter: \( P = a + b + c \), where \( a \), \( b \), and \( c \) are the side lengths.
• Area: Use Heron's formula: \[ A = \sqrt{s(s-a)(s-b)(s-c)} \] where \( s \) is the semi-perimeter \( \frac{a+b+c}{2} \).

Interestingly enough, there are some remarkable properties for scalene triangles, namely, the above area expression, called Heron's Formula for the area, which has the great benefit of computing the area the triangle without requiring the calculation of the height explicitly.

Calculating the Area of a Scalene Triangle

Here's how you can find the area of a scalene triangle:

• First, find the semi-perimeter \( s \) using \( s = \frac{a+b+c}{2} \).
• Then, apply Heron's formula to find the area, by plugging in the value of \(s\).

Scalene Triangle vs. Other Triangles

Here's how a scalene triangle compares to other types of triangles:

• Scalene vs. Isosceles: Isosceles triangles have at least two sides equal, while scalene triangles have all sides different.
• Scalene vs. Equilateral: Equilateral triangles have all sides and angles equal, whereas scalene triangles have no equal sides or angles.
• Scalene vs. Obtuse: A scalene triangle can be obtuse if one of its angles is greater than 90 degrees.

Examples of Scalene Triangles

Here are some examples of scalene triangles:

• A triangle with sides of 3 cm, 4 cm, and 5 cm.
• A triangle with angles of 40°, 60°, and 80°.

Notice that a scalene triangle can also be a right triangle, which is the case of the scalene triangle with sides of 3 cm, 4 cm, and 5 cm.

Can a Scalene Triangle be Obtuse?

Yes, a scalene triangle can be obtuse. An obtuse triangle has one angle greater than 90 degrees, and since all angles in a scalene triangle are different, one of them can certainly be obtuse.

What are the Angles in a Scalene Triangle?

The angles in a scalene triangle are:

• Always different from each other.
• Can be acute, right, or obtuse.
• The sum of all angles is always 180 degrees.

Scalene Triangle in Geometry

What are the uses of scalene triangles? In geometry, scalene triangles are used to:

• Study properties of triangles with no equal sides or angles.
• Explore the concept of triangle inequality.
• Understand the relationship between sides and angles in non-regular polygons.

A scalene triangle is to certain degree a sort of a "typical" triangle, which lacks of any special symmetry, and requires an as generic as it comes treatment.

FAQs on Scalene Triangles

What are the 3 properties of a scalene triangle?

The three main properties of a scalene triangle are:

• All sides are of different lengths.
• All angles are different.
• It has no lines of symmetry.

What are the 7 types of triangles?

The seven types of triangles based on their sides and angles include:

• Scalene
• Isosceles
• Equilateral
• Acute
• Right
• Obtuse
• Equiangular

What is a scalene vs obtuse triangle?

A scalene triangle has all sides of different lengths, while an obtuse triangle has one angle greater than 90 degrees. A scalene triangle can be obtuse if one of its angles exceeds 90 degrees.

Scalene triangle formula

The key formulas for a scalene triangle include:

• Perimeter: \( P = a + b + c \)
• Area: Heron's formula \[ A = \sqrt{s(s-a)(s-b)(s-c)} \]

Scalene triangle pronunciation

The word "scalene" is pronounced as skay-leen.

Scalene triangle angles

In a scalene triangle, all angles are different, and their sum is always 180 degrees.

Scalene triangle area

The area of a scalene triangle can be calculated using Heron's formula:

\[ A = \sqrt{s(s-a)(s-b)(s-c)} \]

Scalene triangle anatomy

The anatomy of a scalene triangle includes:

• Three unequal sides.
• Three different angles.
• No lines of symmetry.

Example of scalene triangle

An example of a scalene triangle would be one with sides measuring 3 cm, 4 cm, and 5 cm.

Scalene triangle properties

The properties of a scalene triangle include:

• All sides are unequal.
• All angles are different.
• No lines of symmetry.

Acute scalene triangle

An acute scalene triangle has all three angles less than 90 degrees, and all sides are of different lengths.

Explore More Triangle Calculators

When dealing with different types of triangles, understanding their unique properties can be quite beneficial. For instance, if you're curious about triangles with all sides of equal length, our Equilateral Triangle Calculator can help you explore their symmetrical beauty and calculate their properties with ease.

On the other hand, if you're working with a triangle where all sides are known, our Triangle Calculator with three sides known will provide you with all the necessary angles and area calculations.

Additionally, if your triangle has one right angle, our Right Triangle Calculator can be particularly useful for understanding the relationship between its sides and angles, which is fundamental in many areas of geometry and trigonometry. Each of these calculators offers a unique perspective on triangles, enhancing your understanding of their geometric properties.