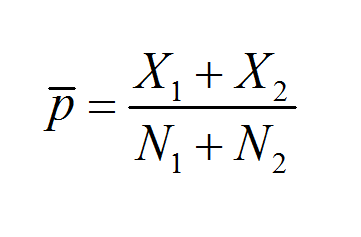Калькулятор пропорций

Этот калькулятор поможет вам с расчетом соотношения пропорциональности A / B = C / D, для которого вам нужно предоставить три из четырех числовых выражений, чтобы найти недостающее. Также вы можете предоставить все четыре из них, и в этом случае калькулятор оценит, выполняется ли пропорциональность для предоставленных чисел.

После того, как вы предоставите запрошенные числовые выражения (которые могут быть числами или любым допустимым числовым выражением), вы можете нажать кнопку "Рассчитать", чтобы увидеть результат вычислений.

Как пользоваться этим калькулятором пропорций?

Использование этого калькулятора пропорций упростит для вас решение математических пропорций. Вот шаги, которые вам следует выполнить:

• Определите пропорциональность: Установите пропорцию, которую вам нужно вычислить
• Введите известные значения: Введите известные значения в предоставленные поля. Вам понадобятся три из четырех чисел, участвующих в пропорции.
• Рассчитать: Нажмите кнопку "Рассчитать", чтобы получить результат. Калькулятор покажет вам недостающее значение.

Шаги по решению пропорций

Вот как можно вручную решать пропорции:

• Установите пропорцию: Запишите соотношения в виде дробей, например \(\frac{A}{B} = \frac{C}{D}\).
• Перекрестное Умножение: Умножьте числитель первой дроби на знаменатель второй и наоборот: \(A \times D = B \times C\).
• Решите неизвестное: Если вы ищете \(x\), переставьте уравнение так, чтобы выделить \(x\).
• Проверьте Свою Работу: Убедитесь, что соотношения равны, подставив найденное значение обратно в исходную пропорцию.

Объяснение формулы пропорции

Основная формула пропорции:

\[ \frac{A}{B} = \frac{C}{D} \]

Где \(A\) и \(B\) — это первое отношение, а \(C\) и \(D\) — это второе отношение. Эту формулу можно также выразить как произведение \(B \times C\)) равным произведению \(A \times D\)). Это отношение играет фундаментальную роль в понимании того, как работают пропорции.

Типы пропорций

Существует несколько типов пропорций:

• Прямая Пропорция: Когда одно количество увеличивается, другое увеличивается с той же скоростью. Например, если вы удваиваете количество рабочих, то и проделанная работа удваивается.
• Обратная Пропорция: При увеличении одной величины другая уменьшается. Например, если вы увеличиваете скорость движения, время достижения пункта назначения уменьшается из-за физической формулы время = расстояние / скорость.
• Разделительная Пропорция: Используется при делении целого на части в соответствии с заданными соотношениями.

Прямая пропорция против обратной пропорциональности

Очень важно понять количественную разницу между прямыми и обратными пропорциями:

• Прямая Пропорция: Когда \(x\) прямо пропорционально \(y\), мы имеем \(x = ky\), где \(k\) — константа.
• Обратная Пропорция: Когда \(x\) обратно пропорционально \(y\), мы имеем \(xy = k\), где \(k\) — константа.

Применение пропорций в реальной жизни

Пропорции — это не просто теоретическая конструкция, они могут иметь множество практических применений, включая:

• Приготовление: Масштабирование рецептов в зависимости от количества порций.
• Финансы: Расчет процентных ставок или доходности инвестиций.
• Строительство: Определение количества материалов, необходимых для проекта.
• Лекарство: Расчет дозировки производится на основе веса и возраста пациента.

Как рассчитать пропорцию?

Чтобы рассчитать пропорцию:

• Определите известные значения в пропорции.
• Составьте уравнение пропорции.
• Используйте перекрестное умножение для нахождения неизвестного.
• Проверьте свое решение, подставив его обратно в исходное уравнение.

Образуют ли соотношения 14:7 и 8:4 пропорцию?

Нам нужно это проверить:

\[ \frac{14}{7} = \frac{8}{4} \]

Упрощая, получаем просто:

\[ 2 = 2 \]

что подразумевает, что обе стороны равны. Так что, да, соотношения 14:7 и 8:4 образуют пропорцию, потому что они равны при упрощении.

Образуют ли 15, 2 и 4/30 пропорцию?

Для проверки:

\[ \frac{15}{2} = \frac{4}{30} \]

Упрощая:

\[ \frac{15}{2} = 7.5 \] \[ \frac{4}{30} = \frac{2}{15} = 0.1333 \]

Поэтому ответ — НЕТ, они не образуют пропорцию, поскольку соотношения не равны.

Калькулятор пропорций с шагами

Вот как работает наш калькулятор пропорций с шагами:

• Введите известные значения, обычно это 3 из 4 значений.
• Калькулятор покажет пошаговый процесс решения пропорции на основе предоставленных входных данных, включая все необходимые перекрестные умножения и решение для неизвестной переменной.
• Он предоставит окончательный ответ для неизвестного значения, а также шаги, предпринятые для получения ответа.

Калькулятор пропорций с 2 переменными

При работе с двумя переменными в пропорции ситуация немного иная, поскольку вы не можете сразу найти решение относительно одной переменной, а скорее выразите одну из неизвестных через другую:

• Шаг 1: Вам необходимо составить уравнение с известными значениями и переменными.
• Шаг 2: Затем вы используете алгебраические преобразования, чтобы выразить одну переменную через другую.
• Шаг 3: Наконец, вам нужно ввести известное значение, чтобы найти неизвестную переменную.

Калькулятор пропорции дроби

Часто вы можете рассматривать пропорции как дроби Калькулятор пропорций дробей помогает:

• Преобразование дробей в десятичные дроби или проценты для более удобного сравнения.
• Проверка эквивалентности дробей путем их упрощения.
• Решение неизвестных дробей в пропорции.

Пропорции в математике

Вы обнаружите, что пропорции играют важную роль в различных областях математики, включая следующие:

• Геометрия: Подобные треугольники и масштабирование напрямую применяют пропорции между сторонами
• Алгебра: Решение уравнений, включающих соотношения. Это также может произойти в исчислении, когда имеешь дело с соответствующими ставками
• Статистика: Используется для понимания различных пропорциональных отношений в наборах данных. Обычно анализируется в форме выборочных пропорций.

Понимая и применяя пропорции, вы можете с легкостью решать сложные математические задачи и реальные сценарии. Независимо от того, корректируете ли вы рецепт, рассчитываете финансовую прибыль или масштабируете чертеж, пропорции — ваш математический союзник.

Больше калькуляторов пропорций

Если вы работаете с пропорциями, вам может быть полезно также наткнуться на смежные области, такие как образцы пропорций. Наши Калькулятор Пропорции Образца может помочь вам понять, как работают и рассчитываются пропорции в выборке, что особенно полезно при статистическом анализе или при работе с опросами и голосованиями.

Кроме того, если ваша работа связана с финансовым анализом, бизнес-показателями или вы просто хотите начать работу с финансовыми отчетами и их интерпретацией, наши Калькулятор Коэффициента Быстрой Ликвидности может быть интересен. Это помогает оценить способность компании выполнять свои краткосрочные обязательства с помощью наиболее ликвидных активов, что косвенно связано с пониманием пропорций в финансовом плане.

Наконец, для тех, кто часто конвертирует разные формы чисел, наш Калькулятор доли в процентах и Калькулятор процентов к дробям может упростить эти преобразования, гарантируя вам наличие нужных инструментов для работы с пропорциями в различных форматах.