Solving Logarithmic Equations
Solving Logarithmic Equations is something you will have to do often when dealing with algebraic procedures, and it is worth to developing a concrete strategy to deal with them.
![]() What you will learn in this tutorial is the main strategies you need to follow to solve logarithmic equations.
What you will learn in this tutorial is the main strategies you need to follow to solve logarithmic equations.
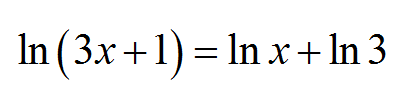
What is logarithmic equation?
The first thing we need to is to define what a logarithmic equation is.
![]() A logarithmic equation is an equation which involves at least one unknown variable, where a logarithmic expression appears in at least one side of the equation
.
A logarithmic equation is an equation which involves at least one unknown variable, where a logarithmic expression appears in at least one side of the equation
.
An example of a logarithmic equation is
\[\ln x = 2\ln x - \ln 3\]or also
\[ \ln(3x-1) - \ln(2x + 1) = 1\]
![]() Notice that a logarithmic equation can contain more than one unknown, like for example
Notice that a logarithmic equation can contain more than one unknown, like for example
Strategies for Solving Logarithmic Equations
The first disclaimer is that there are no bullet-proof ways of solving a logarithmic equation, nor a general equation for that matter. The reason for that is all methods assume a certain structure in the equation, that is not necessarily there in all equations.
So, we cannot find THE way of solving logarithmic equations, because there is no one way that will deal with all possible cases.
Still, there is a couple of strategies to follow that will give you the best chance to go through the equation and find a solution, if one exists.
![]() First, try to group all logarithmic expression into one logarithmic expression.
First, try to group all logarithmic expression into one logarithmic expression.
This is achieved typically by using the most common log rules , that allow you to compact a logarithmic expression, if the structure of the expression allows it so.
![]() Second, once the logarithmic expressions are compacted as much as possible, you will get rid of them, by typically applying the exponential function to both sides of the equality.
Second, once the logarithmic expressions are compacted as much as possible, you will get rid of them, by typically applying the exponential function to both sides of the equality.
This last step, hopefully, will remove all logarithms from the picture, and it will allow you to solve for the unknown(s).
So, in other words, solving a logarithmic equation consists of grouping the logarithmic expressions, eliminating them by applying exponential, and then solve the equation as a regular equation.
Obviously, when you have got rid of the logarithms, you face an equation which could have its own challenges.
Solving different examples of logarithmic equations
There is no better way of learning how to solve equations than actually practice solving them:
EXAMPLE 1:
Solve the following equation:
\[\large 4 \log(\sqrt x) = \log(6x-1)\]ANSWER:
Let us follow the strategies. The idea is to compact the logarithmic expressions as much as possible. This is a judgement call, because the main idea is to essentially get rid of the logarithms.
Using the log rules we can put the "4" inside of the logarithm as
\[\large 4 \log(\sqrt x) = \log(6x-1)\] \[\large \Rightarrow \log((\sqrt x)^4) = \log(6x-1)\] \[\large \Rightarrow \log(x^2) = \log(6x-1)\]Now that the logarithmic expressions are as compacted as possible, we need to get rid of the logarithms.
One way of doing it is to apply the exponential function \(10^x\) to each side of the equality. What do I mean by that???
Well, you have two sides in that equality. Since both sides are the same, when used as arguments of the function \(10^x\), it should preserve the equality. So we have
\[\large \log(x^2) = \log(6x-1)\] \[\large \Rightarrow 10^{\log(x^2)} = 10^{\log(6x-1)}\] \[\large \Rightarrow x^2 = 6x-1\]because we know that \(10^{\log a} = a\), which is one of the basic log rules.
So now that we have eliminated the logarithms, we can solve the equation that is left:
\[\large x^2 = 6x-1\] \[\large \Rightarrow x^2 - 6x + 1 = 0\] \[\large \Rightarrow x = \frac{-(-6) \pm \sqrt{(-6)^2-4(1)(1)}}{2(1)}\] \[\large \Rightarrow x = \frac{6 \pm \sqrt{36-4}}{2}\] \[\large \Rightarrow x = \frac{6 \pm \sqrt{32}}{2}\] \[\large \Rightarrow x = \frac{6 \pm 4\sqrt{2}}{2}\] \[\large \Rightarrow x = 3 \pm 2\sqrt 2\]so then \(x_1 = 3 + 2\sqrt 2\) and \(x_2 = 3 - 2\sqrt 2\). Technically, you need to check whether these two are solutions of the original equation, so to make sure they belong to the domain of the logarithmic expressions.
In this case, both \(x_1 = 3 + 2\sqrt 2\) and \(x_2 = 3 - 2\sqrt 2\) are the solutions of the original equation.
EXAMPLE 2:
Solve the following logarithmic equation:
\[\large \ln 5 - \ln(6-x) = \ln x\]ANSWER:
Using the log rules we can compact the log expressions, we get that
\[\large \ln 5 - \ln(6-x) = \ln x\] \[\large \displaystyle \Rightarrow \ln\left(\frac{5}{6-x}\right) = \ln x\] \[\large \displaystyle \Rightarrow e^{\ln\left(\frac{5}{6-x}\right)} = e^{\ln x}\] \[\large \displaystyle \Rightarrow \frac{5}{6-x} = x\]because we know that \(e^{\ln a} = a\), which is one of the basic log rules.
Therefore, now that we have eliminated the logarithms, we can solve the equation that we have left:
\[\large \displaystyle \frac{5}{6-x} = x\] \[\large \displaystyle \Rightarrow 5 = x(6-x)\] \[\large \displaystyle \Rightarrow 5 = 6x - x^2\] \[\large \displaystyle \Rightarrow x^2 -6x + 5 = 0\] \[\large \displaystyle \Rightarrow (x-1)(x-5) = 0\]so then \(x_1 = 1\) and \(x_2 = 5\). Let us plug these values into the original equation to see if they are in fact solutions:
![]() For \(x_1 = 1\):
For \(x_1 = 1\):
which is the same as:
\[\large \ln 5 - \ln(5) = 0\]which is true, so the equation holds.
![]() For \(x_1 = 5\):
For \(x_1 = 5\):
which is the same as:
\[\large \ln 5 - \ln(1) = \ln(5)\]which is true, so the equation holds.
Therefore, the solutions to the equation are \(x_1 = 1\) and \(x_2 = 5\).
More About Solving Logarithmic Equations
One thing that students are most concerned about is how do you get rid of log in an equation. But we have seen that is actually the easy part. What is harder is to actually algebraically work the expression so that the logs can be removed.
That brings up the question of how to deal with different bases, which requires its own paragraph.
Solving logarithmic equations with different bases
In the above examples we only dealt with \(\log\) (logarithm with base 10) and \(\ln\) (logarithm with base \(e\)). How do you do it when you have a logarithm with a different base, like \(\log_a\)???
The answer is simple: In order to eliminate logarithms with a different base, say \(\log_a\) which has base \(a\) we simply use the exponential function \(a^x\). Simple right??
Indeed, eliminating the logarithm is the easy part of solving log equations. The harder part of the process is to group and compact the logarithmic expressions in a form that you eliminate them.
You can learn more about how the logarithmic function works by seeing the properties of its graph and studying the basic log rules .
