सर्कल का समीकरण
एक सर्कल सबसे उल्लेखनीय ज्यामितीय आंकड़ों में से एक है।इसमें कुछ उल्लेखनीय समरूपता है, इस तथ्य के आधार पर कि सर्कल में सभी बिंदु केंद्र से समान हैं, जिसका अर्थ है कि सर्कल के सभी बिंदु केंद्र से समान दूरी हैं।यह सामान्य दूरी \(r\) कहा जाता है सराय ।
सर्कल में कुछ महत्वपूर्ण ज्यामितीय अनुप्रयोग हैं, जो इसे ज्यामिति और बीजगणित दोनों में वास्तव में महत्वपूर्ण वस्तु बनाते हैं।
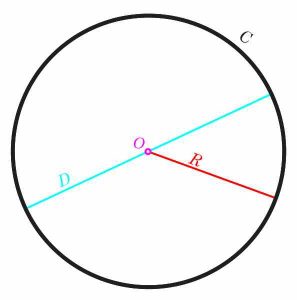
सर्कल की एक और महत्वपूर्ण संपत्ति यह है कि यह बहुत आसानी से बीजगणितीय रूप से प्रतिनिधित्व करता है।इसका मतलब है कि हम किसी दिए गए सर्कल में सभी बिंदुओं का प्रतिनिधित्व करने के लिए आसानी से एक समीकरण सेट कर सकते हैं।इसे और अधिक संलग्न करने के लिए, निर्देशांक विमान \(X - Y\) पर विचार करें।इसका मतलब यह है कि हमारे पास एक्स और वाई एक्सिस हैं, जो एक दूसरे के लिए लंबवत हैं
सर्कल का समीकरण
अब, हम उस समीकरण के बारे में बात करते हैं जो किसी दिए गए सर्कल के सभी बिंदुओं का प्रतिनिधित्व करता है।दरअसल, त्रिज्या के एक सर्कल के लिए \(r\), निम्नलिखित समीकरण में अंक का वर्णन है \((x, y)\) जो सर्कल पर हैं:
\[\Large x^2 + y^2 = r^2\]उपरोक्त त्रिज्या के एक सर्कल के समीकरण से मेल खाती है \(r\), CENTER पर स्थित है, \((0,0)\), समन्वय अक्षों की उत्पत्ति।
जब त्रिज्या \(r = 1\) है, तो हमारे पास वह है जिसे कहा जाता है व rayrत ।
उपरोक्त समीकरण को देखते समय, ज्यामितीय व्याख्या यह है कि \(x\) और \(y\) एक त्रिभुज के पक्ष हैं और \(r\) इसका हाइपोटेनस है
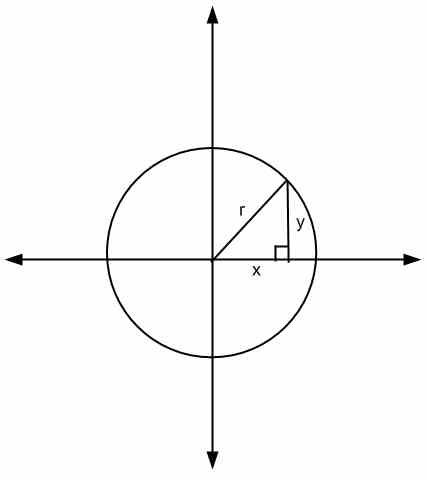
सर्कल के समीकरण को देखने का एक और तरीका समीकरण के दोनों किनारों पर वर्गमूल को ले जाना है, इसलिए हमें \(\sqrt{x^2+y^2} = r\) मिलेगा, जो इंगित करता है कि किसी भी बिंदु के लिए \((x,y)\) सर्कल पर, । (इस मामले में, सर्कल का केंद्र) \(r\) के बराबर है।
एक सर्कल का समीकरण जो मूल में केंद्रित नहीं है
समन्वित कुल्हाड़ियों पर काम करने का एक फायदा यह है कि सर्कल पर अंक, और केंद्र, हो सकता है तमाम कुल्हाड़ियों में, और एक समीकरण द्वारा प्रतिनिधित्व किया जा सकता है, जैसा कि ऊपर दिखाया गया है।लेकिन सामान्य तौर पर, सर्कल के केंद्र को मूल होने की आवश्यकता नहीं है, यह समन्वित अक्षों में कोई भी बिंदु \((x_0, y_0\) हो सकता है, जिस स्थिति में, सर्कल का समीकरण बन जाता है:
\[\Large (x-x_0)^2 + (y-y_0)^2 = r^2\]जिसे के रूप में जाना जाता है अफ़र्याश ।उदाहरण के लिए, कहते हैं कि आपको त्रिज्या के एक सर्कल के समीकरण की गणना करने की आवश्यकता है \(r = 4\), जो कि बिंदु पर केंद्रित है \((1,2)\)।तो इस मामले में, हमारे पास \(x_0 = 1\), \(y_0 = 2\) और \(r = 4\) है, और फिर हम इन नंबरों को उपरोक्त समीकरण में प्लग करते हैं और हम प्राप्त करते हैं
\[\large (x-1)^2 + (y-2)^2 = 4^2\]या हम भी लिख सकते हैं
\[\large (x-1)^2 + (y-2)^2 = 16\]उदाहरण 1
मूल में केंद्र के साथ त्रिज्या 3 के सर्कल के समीकरण को लिखें।समीकरण का उपयोग करना, यह निर्धारित करें कि बिंदु (1, 2) सर्कल से संबंधित है या नहीं।
उत्तर:
सबसे पहले, हम सर्कल के समीकरण को निर्धारित करते हैं।इस मामले में, सर्कल मूल में केंद्रित है, इसलिए \((x_0, y_0) = (0, 0)\)।इसलिए, समीकरण है
\[\large x^2 + y^2 = 3^2\]जो वैसा ही है
\[\large x^2 + y^2 = 9\]अब, सवाल यह है कि क्या बिंदु (1, 2) सर्कल पर है या नहीं।हम जानते हैं कि सर्कल पर अंक ऐसे होंगे जो \(x^2 + y^2 = 9\)।
बिंदु के लिए \((1, 2)\) हमें लगता है कि \(x = 1\) और \(y=2\), तो उस बिंदु के इस मामले के लिए, \(x^2 + y^2 = 1^2 + 2^2 = 1+ 4 = 5\) जो 9 से अलग है, और इसलिए \((1,2)\)>सर्कल से संबंधित नहीं है।
सर्कल के समीकरण के बारे में अधिक
सर्कल एक महत्वपूर्ण गणित इकाई है, कि पुस्तक के संस्करणों को इसके बारे में लिखा गया है।सर्कल ज्यामिति, त्रिकोणमिति और बीजगणित को पार करते हैं, इसलिए यह गणित में हर जगह ट्रांसवर्सल उपस्थिति के रूप में है।
एक सर्कल के समीकरण को कैसे काम करें?
जब हम एक सर्कल के साथ काम करते हैं, तो काम करने के लिए कई चीजें होती हैं।पहली बात सर्कल के समीकरण का निर्माण करना है।उदाहरण के लिए, त्रिज्या के एक सर्कल पर विचार करें \(r = 3\), जो कि बिंदु पर केंद्रित है \((1,1)\)।
एक सर्कल के सामान्य समीकरण के आधार पर, समीकरण है
\[\large (x-1)^2 + (y-1)^2 = 3^2\]उपरोक्त समीकरण का उपयोग किया जा सकता है, उदाहरण के लिए, यह निर्धारित करने के लिए कि एक बिंदु सर्कल से संबंधित है या नहीं।सर्कल के समीकरण को बाहर करने के लिए आप और क्या कर सकते हैं?आप संभावित रूप से वर्गों का विस्तार कर सकते हैं, इसलिए हमें मिलता है
\[\large x^2 - 2x + 1 + y^2 -2y + 1 = 9\]जिसे सरल किया जा सकता है
\[\large x^2 - 2x + y^2 -2y = 7\]इसलिए, दोनों समीकरण समकक्ष हैं, इस अर्थ में कि वे एक ही सर्कल का निर्धारण करते हैं।आपको कौन सा पसंद है?\((x-1)^2 + (y-1)^2 = 3^2\) या \(x^2 - 2x + y^2 -2y = 7\)?यह स्वाद की बात है और आप किस लिए सूत्र का उपयोग करेंगे।
एक सर्कल का क्षेत्र
दिलचस्प बात यह है कि गणना करने के लिए एक raurcun kadauthir , आपको पूर्ण समीकरण की आवश्यकता नहीं है, आपको बस त्रिज्या जानने की आवश्यकता है।दूसरे शब्दों में, एक वृतthun kadauraur कry इसके केंद्र पर निर्भर न हों।
क्या एक सर्कल का समीकरण एक फ़ंक्शन है?
यह एक ऐसा सवाल है जो कई छात्रों के पास है, और हमें स्पष्ट करने की आवश्यकता है।सबसे पहले, सराय एक समीकरण है, एक संबंध या एक फ़ंक्शन नहीं।
अब, सर्कल का समीकरण एक संबंध निर्धारित करता है, और नहीं तमाम , जब आप बीजगणितीय रूप से X के rurcaus में y के हल हल क क क ।वास्तव में, अगर हम \(y\) के लिए हल करते हैं तो हमें मिलता है:
\[\large x^2 + y^2 = 9 \Rightarrow y^2 = 9 - x^2 \] \[\large \Rightarrow y = \pm \sqrt{ 9 - x^2} \]इसका मतलब है कि किसी दिए गए \(x\) के लिए, \(y\) के दो मान हैं जो जुड़े हुए हैं, जो \(\sqrt{ 9 - x^2}\) और \(-\sqrt{ 9 - x^2}\) हैं, जो इंगित करता है कि सर्कल का समीकरण एक निर्धारित करता हैएक फ़ंक्शन के बजाय संबंध।
सर्कल का एक विशिष्ट मामला है व rayrत , समीकरण के साथ \(x^2 + y^2 = 1\), जो मूल में केंद्रित है।यूनिट सर्कल विशेष रूप से काम करने के लिए उपयुक्त है तmur अभिव बहुत ही दृश्य तरीके से।
