كيف تجد المدى
يمكن أن يثبت تعلم كيفية العثور على نطاق دالة ما أنه مهم جدًا في الجبر وحساب التفاضل والتكامل , لأنه يمنحك القدرة على تقييم القيم التي تصل إليها الدالة. أو بمعنى آخر , يسمح لك بالعثور على مجموعة جميع الصور عبر الوظيفة
مهمة العثور على النقاط التي يمكن الوصول إليها بواسطة دالة هي مهمة مفيدة للغاية. على سبيل المثال , قد يكون لديك دالة إنتاج \(q(x)\) , والتي تمنحك مقدار المخرجات التي تم الحصول عليها لوحدات الإدخال \(x\).
نرغب في معرفة عدد وحدات الإدخال المطلوبة لإنتاج \(b\) وحدات من المخرجات. بمعنى آخر , نحتاج إلى إيجاد \(x\) بحيث \(q(x) = b\) , وهي طريقة أخرى للسؤال عما إذا كان \(b\) يقع في نطاق الدالة \(q(x)\) أم لا.
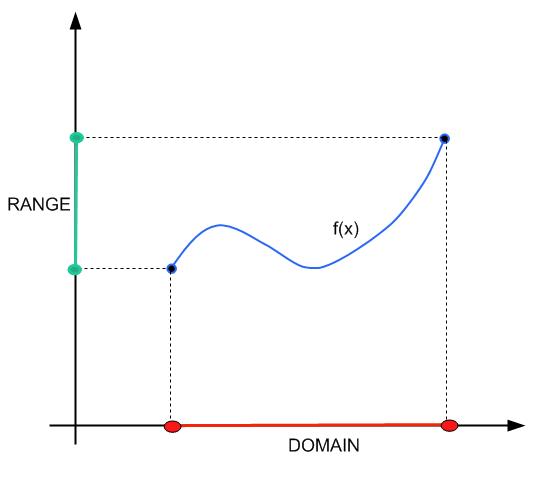
في هذا البرنامج التعليمي سوف نركز أكثر على آليات إيجاد النطاق. للحصول على نهج مفاهيمي أكثر للمجال والنطاق , يمكنك ذلك تحقق من هذا البرنامج التعليمي .
الطريقة الجبرية لإيجاد مدى دالة
كما هو الحال عندما تعلمنا كيفية حساب المجال , لا توجد وصفة واحدة للعثور على النطاق , إنها تعتمد حقًا على بنية الوظيفة \(f(x)\).
ومع ذلك , هناك تقنية جبرية واحدة سيتم استخدامها دائمًا. هذه هي الطريقة التي تجد بها النطاق. انتبه:
لنفترض أننا بحاجة إلى الحصول على نطاق دالة معينة \(f(x)\). بعد ذلك , سننظر في رقم حقيقي عام \(y\) وسنحاول حل \(x\) المعادلة التالية:
\[f(x) = y\]نحتاج إلى تحديد قيم \(y\) التي يمكن حل المعادلة أعلاه لـ \(x\). هذا هو. بالطبع , قد يكون من الصعب القيام بذلك , اعتمادًا على هيكل الوظيفة \(f(x)\) , ولكن هذا ما عليك القيام به.
إذن فهذه هي الطريقة الجبرية , طريقة إيجاد مدى دالة بدون رسم بياني.
مثال 1
ابحث عن نطاق الوظيفة \(\displaystyle f(x) = \frac{x+1}{x-3}\):
إجابه:
ننتقل باستخدام الطريقة الجبرية: لنفترض أن \(y\) يكون رقمًا وسنحل مشكلة \(x\) في المعادلة التالية: \(f(x) = y\). تقع القيمة \(y\) في النطاق إذا كان من الممكن حل \(f(x) = y\) من أجل \(x\).
في هذه الحالة لدينا:
\[\large f(x) = y \Leftrightarrow \frac{x+1}{x-3} = y\] \[\Rightarrow \,\,\,x+1 = y\left( x-3 \right)\] \[\Rightarrow \,\,\,x+1 = yx-3y\] \[\Rightarrow \,\,\,x-yx=-1-3y\] \[\Rightarrow \,\,\,x\left( 1-y \right)=-1-3y\] \[\Rightarrow \,\,\,x=\frac{3y+1}{y-1}\]لذلك , متى سيتم تحديد \(x\) تحديدًا جيدًا؟ تقريبًا لجميع \(y\) , باستثناء الوقت \(y = 1\) , لأنه في هذه الحالة لدينا قسمة على \(0\). ومن ثم , فإن نطاق \(f\) في هذه الحالة هو الخط الحقيقي بالكامل , باستثناء 1.
إذا استخدمنا تدوين الفاصل الزمني , فيمكننا كتابة \(Range(f) = (-\infty, 1) \cup (1, +\infty)\).
مثال 2
ابحث عن نطاق الوظيفة \(f(x) = x^2 - 4x + 3\):
إجابه:
مرة أخرى , نواصل استخدام الطريقة الجبرية , حتى تعرف التمرين: دع \(y\) يكون رقمًا وسنحل لـ \(x\) في المعادلة التالية: \(f(x) = y\). تقع القيمة \(y\) في النطاق إذا كان من الممكن حل \(f(x) = y\) من أجل \(x\).
في هذه الحالة لدينا:
\[\large f(x) = y \Leftrightarrow x^2 - 4x + 3 = y\] \[\Rightarrow \,\,\, x^2 - 4x + 3 - y = 0 \text{ (This is a quadratic equation in x)}\] \[\Rightarrow \displaystyle \,\,\, x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\] \[\Rightarrow \displaystyle \,\,\, x = \frac{-(-4) \pm \sqrt{(-4)^2 - 4(1)(3-y)}}{2(1)}\] \[\Rightarrow \displaystyle \,\,\, x = \frac{4 \pm \sqrt{16 - 4(3-y)}}{2}\] \[\Rightarrow \displaystyle \,\,\, x = \frac{4 \pm \sqrt{16 - 12 + 4y}}{2}\] \[\Rightarrow \displaystyle \,\,\, x = \frac{4 \pm \sqrt{4 + 4y}}{2}\] \[\Rightarrow \displaystyle \,\,\, x = 2 \pm \sqrt{1+y}\]الآن , برؤية هذا التعبير النهائي , متى سيتم تعريف \(x\) جيدًا؟ نحتاج إلى أن تكون سعة الجذر التربيعي غير سالبة , لذا فنحن بحاجة إلى:
\[1+y \ge 0\]مما يعني أن \(y \ge -1\). إذا استخدمنا تدوين الفاصل الزمني , فيمكننا كتابة \(Range(f) = [-1, +\infty)\).
في هذا المثال , كان بإمكاننا حلها باستخدام حقيقة أن \(f(x) = x^2 - 4x + 3\) دالة تربيعية , وأن رسمها البياني عبارة عن قطع مكافئ يفتح لأعلى.
يتم الوصول إلى النقطة الدنيا لهذا القطع المكافئ عند الرأس. إحداثي س للرأس هو:
\[\displaystyle x_V = \frac{-b}{2a} =\frac{-(-4)}{2(1)} =\frac{4}{2} = 2\]الآن , يمكن إيجاد إحداثي y للرأس ببساطة عن طريق إدخال القيمة \(x_V = 2\) في الدالة التربيعية:
\[y_V = f(x_V) = 2^2 - 4(2) + 3 = -1\]نظرًا لأن القيمة الدنيا التي تم الوصول إليها بواسطة القطع المكافئ هي \(-1\) , فإننا نستنتج أن النطاق هو \([-1, +\infty)\) , وهو نفس النتيجة التي تم العثور عليها جبريًا.
الرسم البياني للوظيفة \(f(x) = x^2 - 4x + 3\) يجعل الأمر أكثر وضوحًا:
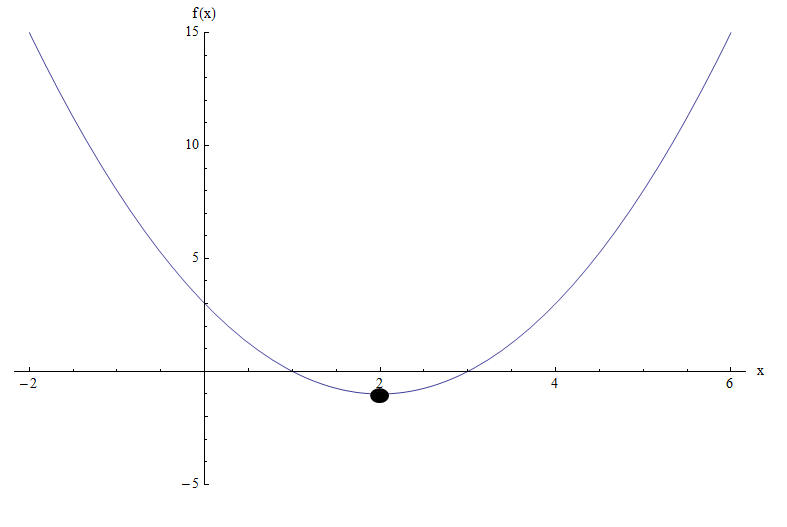
يمكننا أن نرى أنه , بناءً على الرسم البياني , تم الوصول إلى الحد الأدنى عند \(x = 2\) , وهو بالضبط ما تم العثور عليه في الإحداثي x للرأس.
تتمثل مخاطر استخدام الرسم البياني للعثور على النطاق في احتمال إساءة قراءة النقاط الحرجة في الرسم البياني وإعطاء تقييم غير دقيق للمكان الذي تصل فيه الوظيفة إلى الحد الأقصى أو الحد الأدنى.
استراتيجيات أخرى لإيجاد مدى دالة
كما رأينا في المثال السابق , يمكننا أحيانًا إيجاد نطاق دالة بمجرد النظر إلى الرسم البياني الخاص بها.
على سبيل المثال , لنفترض أنك تريد العثور على نطاق الوظيفة \(f(x) = x + 3\). يظهر الرسم البياني أدناه:
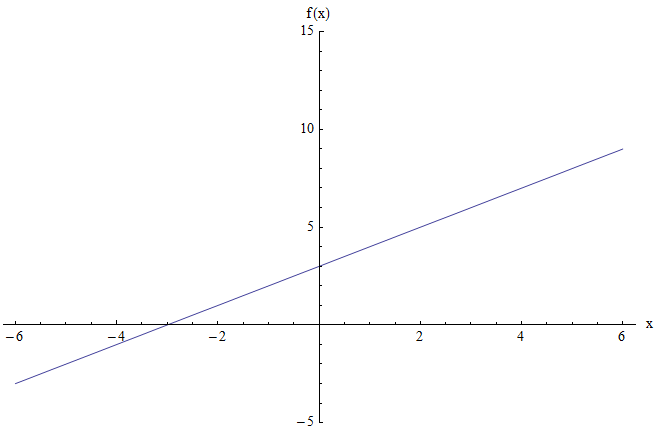
لا يُظهر الرسم البياني أعلاه أي حد أدنى أو أقصى للنقاط. علاوة على ذلك , عندما تكون \(x\) كبيرة وموجبة , تكون قيمة الوظيفة أيضًا كبيرة وموجبة. وبالمثل , عندما تكون \(x\) سالبة جدًا , تكون قيمة الدالة سالبة جدًا أيضًا.
الحدس هو أن الوظيفة يمكن أن تأخذ قيمًا سلبية وإيجابية كما نريد , عن طريق تحديد قيم \(x\) كبيرة بما يكفي (إيجابية أو سلبية). وبعد ذلك , الخلاصة هي أن النطاق هو الخط الحقيقي بأكمله , وهو \((-\infty, +\infty)\) باستخدام تدوين الفترة.
مثل هذا التحليل صحيح من حيث النتيجة , لكنه واه من حيث المنطق. توجد هذه المشكلة في "الطريقة الرسومية" للعثور على النطاق: فهي جذابة من وجهة نظر بديهية , لكنها ضعيفة نوعًا ما من حيث المحتوى.
عادة , إذا أمكن , يجب أن نفضل الطريقة التحليلية / الجبرية. في المثال , نحتاج إلى حل مشكلة \(x\):
\[x + 3 = y\] \[\Rightarrow \,\, x = y - 3\]إذن , هل هناك أي قيود على \(y\) لكي يتم تعريف \(x\) جيدًا؟ لا على الإطلاق , إذن , لا توجد قيود على \(y\) والاستنتاج هو أن النطاق هو الخط الحقيقي بأكمله.
يمكنك التحقق من هذه المقالة التي تريدها تعرف كيف تجد مجال الوظيفة في حين أن.
هناك العديد من الأسباب الجبرية الجيدة لإيجاد النطاق , أحدها لأنه جزء من عمليات إيجاد معكوس دالة .
