الجبر دروس

القطط الأول

Hyperbola هو المكان الرئيسي للنقاط الهندسية في محاور الإحداثيات التي تحتوي على الممتلكات التي يكون لها الفرق بين المسافات إلى نقطتين ثابتتين (بؤر), يساوي ثابتا, والتي ننفها \(2a\).

بطبيعة الحال, هذا يبدو تخويفا بعض الشيء وتقنية للغاية, لكنه في الواقع الطريقة التي يتم بها تعريف hyperbola.

ربما, إذا أعطيتك معادلة Hyperbola, فستتعرف عليها ".

دعونا نحاول: هذه هي معادلة Hyperbola العامة للغاية:

\[\large \displaystyle \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 \]

هل يمكن أن تكتشف كيف تبدو عن طريق التحقق من معادلاتها فقط؟على الاغلب لا.لذلك أنا أعرض Hyperbola, بيانيا لك:

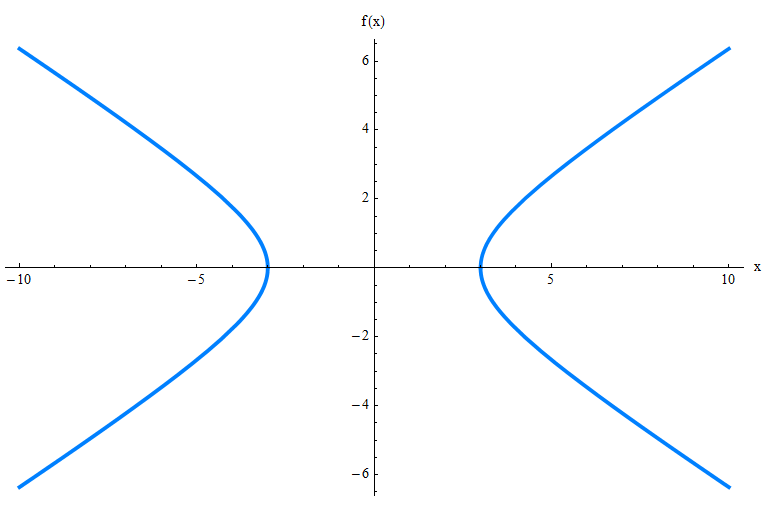
يوضح لك الرسم البياني أعلاه الرسم البياني فقط من HYPERBOLA, ولكن هناك العديد من العناصر الأخرى التي تحتاج إلى أن تكون على دراية بها, مثل المقاييس المائلة, والقمم والبونتي.تحقق من الرسم البياني أدناه.

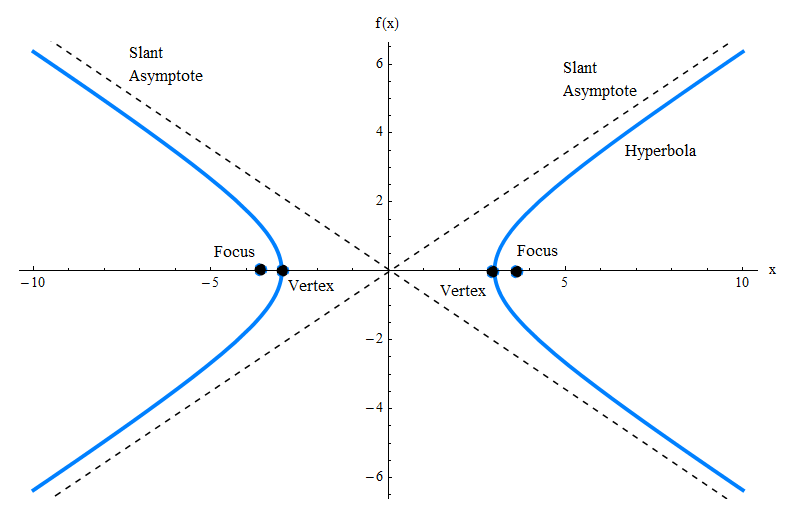
المعادلة العامة لقطyPOLA

بدون الكثير من المناقشة النظرية, سنذكر أن المعادلة العامة لقطyPOLA مع بؤر على المحور X

\[\large \displaystyle \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 \]

بالنسبة للقنفذ الأول الذي وصفه المعادلة المذكورة أعلاه, فإنه يحتوي على رؤوس عند النقاط \((-a, 0)\) و \((a, 0)\) ولديه بؤر في النقاط \((-c, 0)\) و \((c, 0)\), حيث \(c = \sqrt{a^2 + b^2}\).

ميزة مثيرة للاهتمام لهذه القطط الباطنية هي أنه يحتوي على اثنين من المتفظالات المائلة

asymptote 1. : \(\displaystyle y = \frac{b}{a}x\)

asymptote 2. : \(\displaystyle y = -\frac{b}{a}x\)

الآن ما يحدث مع معادلة Hyperbola, إذا تم ترجمة القمم بدلا من ذلك بواسطة نقطة معينة \((k,h)\)؟

كل ما عليك فعله في هذه الحالة هو استبدال \(x\) بواسطة \(x-k\), واستبدال \(y\) بواسطة \(x-h\).

وبالتالي, من خلال القيام ترجمة, نحصل على معادلة Hyperbola العامة

\[\large \boxed{\displaystyle \frac{(x-k)^2}{a^2} - \frac{(y-h)^2}{b^2} = 1 }\]

يحتوي Hyperbola أعلاه على رؤوس عند النقاط \((k-a, h)\) و \((k+a, h)\) ولديه بؤر في النقاط \((k-c, h)\) و \((k+c, h)\), حيث \(c = \sqrt{a^2 + b^2}\).

معادلات الأقاليم المائلة هي \(y = \frac{b}{a}(x-k) + h\) و \(y = -\frac{b}{a}(x-k) + h\).

ماذا يحدث مع القطط الرائعة التي تفتح على طول محور y؟

بالتناظر, كل ما يتعين علينا القيام به هو ببساطة استبدال أدوار \(x\) و \(y\) في المعادلة العامة لقطyPOLA لدينا بالفعل.في التطبيق العملي, هذا يعني أنه أينما يظهر \(x\) في معادلة Parabola لدينا, نقوم بتغييره \(y\), والعكس صحيح بالنسبة ل \(y\).

إذن, في حالة Hyperbola التي تفتح طويل المحور X, المعادلة العامة هي

\[\large \boxed{\displaystyle \frac{(y-h)^2}{b^2} - \frac{(x-k)^2}{a^2} = 1 }\]

يحتوي Hyperbola أعلاه على رؤوس عند النقاط \((k, h - b)\) و \((k, h+b\) ولديه بؤر في النقاط \((k, h-c)\) و \((k, h+c)\), حيث \(c = \sqrt{a^2 + b^2}\).

معادلات الأقاليم المائلة هي \(y = \frac{b}{a}(x-k) + h\) و \(y = -\frac{b}{a}(x-k) + h\).

مثال 1

ابحث عن بؤر, والقمم وأعربطة مائلة من hyperbola:

\[\large \displaystyle \frac{(y-2)^2}{9} - \frac{(x-4)^2}{16} = 1 \]

إجابه:

هذا hyperbola يفتح على طول محور y.في هذه الحالة, قيم الترجمة هي \(k = 4\) و \(h = 2\).أيضا, نحصل على ذلك \(a = \sqrt{16} = 4\) و \(b = \sqrt{9} = 3\).وبالتالي, نحصل على ذلك \(c = \sqrt{a^2+b^2} = \sqrt{4^2+3^2} = \sqrt{25} = 5\).

وبالتالي, فإن البؤر هي \((k, h-c) = (4, 2 - 5) = (4, -3)\) و \((k, h+c) = (4, 2 + 5) = (4, 7)\).

القمم هي \((k, h-b) = (4, 2 - 3) = (4, -1)\) و \((k, h+b) = (4, 2 + 3) = (4, 5)\).

مقطورات مائلة هي

\[\displaystyle y = \frac{b}{a}(x-k) + h = \frac{3}{4}(x-4) + 2\] \[\displaystyle y = -\frac{b}{a}(x-k) + h = \frac{3}{4}(x-4) + 2\]

بيانيا:

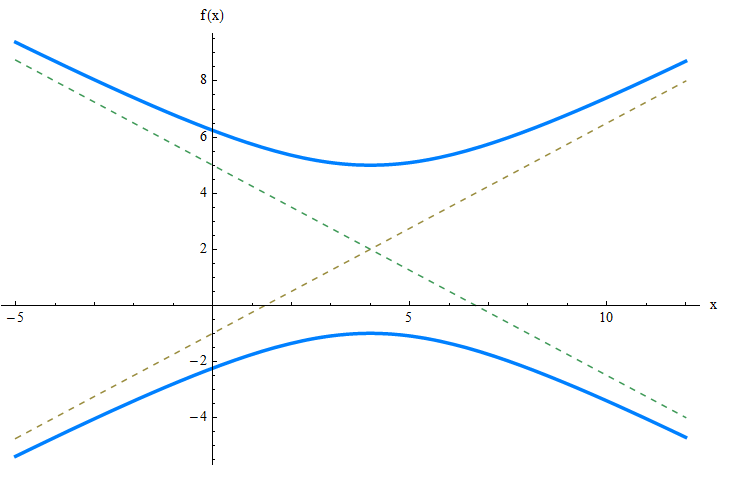
مثال 2

ابحث عن معادلة Hyperbola مع FOUSI في \((-4, 0)\) و \((4, 0)\) Vertex, ركز في \((6, 0\).

إجابه:

لاحظ أن البؤر والأثياء موجودة على المحور X, لذلك ثم يفتح Hyperbola على طول المحور X.أيضا, نظرا لأن البؤر متناظرة فيما يتعلق بالأصل, فستكون قمة واحدة \((4, 0)\), نحصل على ذلك \(a = 4\).وبما أن التركيز واحد في \((6, 0)\), نحصل على ذلك \(b = \sqrt{6^2 - 4^2} = \sqrt{20} = 2\sqrt 5\).

لذلك, معادلة Hyperbola هي:

\[\large \displaystyle \frac{(y-h)^2}{b^2} - \frac{(x-k)^2}{a^2} = 1 \] \[\large \displaystyle \Rightarrow \frac{x^2}{16} - \frac{y^2}{20} = 1 \]

أقسام Hyperbola والمكونات العامة

كما هو الحال مع حالة Parabola, فإن Hyperbola مرتبط بإحكام بالمخروط.في الواقع, فإن علماء الرياضيات اليونانيين يدويون باسم Apollonius هو الشخص الذي اكتشف هذا الاتصال, من خلال فهم مفهوم أقسام مخروطية.

يحدث قسم مخروطي عند قطع مخروط من مخروط بطائرة, واعتمادا على الزاوية النسبية للمخروط والطائرة عند نقطة قطع, يتم قطع المخروط بطريقة يكون بها القسم العرضي شكل محددوبعد

لذلك, اعتمادا على الزاوية النسبية للقطع لدينا أشكال مختلفة من القسم, وهذه هي parabola, دائرة, القطع الناقص, و hyperbola.انظر الرسم البياني أدناه: