关于通过转换为 z 分数进行规范化的更多信息

标准化分数的概念,或者 z分数标准化 相当于计算数据集中所有分数的 z 分数。也就是说,对于数据集中的每个 \(X_i\) 分数,我们按照以下公式计算相应的归一化分数（z 分数）

. \[ X_i = \frac{X_i - \mu}{\sigma}\]

如果不知道总体平均值 \(\mu\) 或总体标准差 \(\sigma\),我们通过计算样本平均值 \(\bar X\) 和样本标准差 \(s\) 来近似它们。

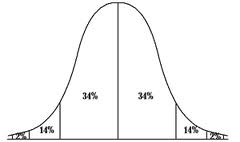
这些标准化的 z 分数响应 标准正态分布 ,并可使用标准正态表或Excel等计算工具轻松计算。

Z 分数的必要性

为什么我们需要标准化分数？标准化分数有很多优点：首先,它们是无量纲的,因此非常适合比较不同的人群。其次,它们往往能提供对量表的清晰解读,就像心理学或其他社会科学中通常的做法一样。

如果您需要计算样本数据的完整描述统计数据,请使用此 完整的描述统计计算器 ,或者如果你使用这个 正态概率计算器 计算和绘制与正常概率相关的任何内容,包括 z 分数概率。