如何查找范围
学习如何找到函数的范围在代数和微积分中被证明是非常重要的,因为它使您能够评估函数达到的值。或者换句话说,它允许您通过函数找到所有图像的集合
寻找函数可以到达哪些点的任务是一项非常有用的任务。例如,您可能有一个生产函数 \(q(x)\),它为您提供了 \(x\) 个单位的输入所获得的输出量。
我们想知道需要多少个输入单元才能产生 \(b\) 个输出单元。所以换句话说,我们需要找到 \(x\) 以便 \(q(x) = b\),这是另一种询问 \(b\) 是否在函数 \(q(x)\) 范围内的方法。
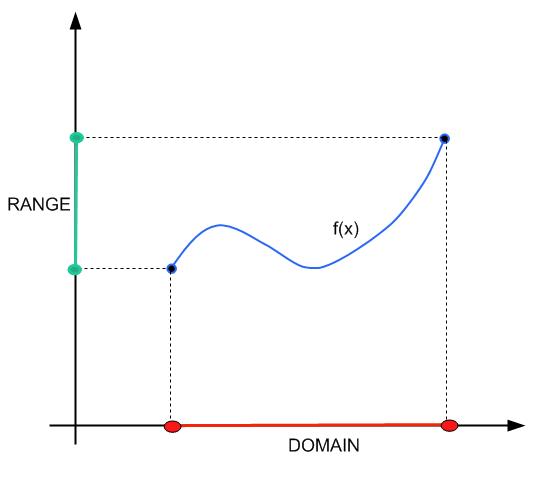
在本教程中,我们将更多地关注寻找范围的机制。对于域和范围的更概念化的方法,您可以 检查本教程 .
求函数范围的代数方法
与我们学习如何计算域时一样,没有一种方法可以找到范围,它实际上取决于函数 \(f(x)\) 的结构。
然而,总有一种代数技术会被使用。这是您找到范围的方式。请注意:
假设我们需要获取给定函数 \(f(x)\) 的范围。然后,我们将考虑一个通用实数 \(y\),我们将尝试求解 \(x\) 以下方程:
\[f(x) = y\]我们需要确定 \(y\) 的哪些值可以为 \(x\) 求解上述方程。这就对了。当然,这可能很难做到,这取决于函数 \(f(x)\) 的结构,但它是您需要做的。
所以这是代数方法,即如何在不绘制图形的情况下找到函数范围的方法。
例 1
求函数 \(\displaystyle f(x) = \frac{x+1}{x-3}\) 的范围:
回答:
我们继续使用代数方法:让 \(y\) 是一个数字,我们将在以下等式中求解 \(x\):\(f(x) = y\)。如果 \(f(x) = y\) 可以求解 \(x\),则 \(y\) 值在范围内。
在这种情况下,我们有:
\[\large f(x) = y \Leftrightarrow \frac{x+1}{x-3} = y\] \[\Rightarrow \,\,\,x+1 = y\left( x-3 \right)\] \[\Rightarrow \,\,\,x+1 = yx-3y\] \[\Rightarrow \,\,\,x-yx=-1-3y\] \[\Rightarrow \,\,\,x\left( 1-y \right)=-1-3y\] \[\Rightarrow \,\,\,x=\frac{3y+1}{y-1}\]因此,\(x\) 什么时候会被明确定义?几乎所有 \(y\),除了 \(y = 1\) 时,因为在这种情况下,我们有一个被 \(0\) 的除法。因此,在这种情况下 \(f\) 的范围是整条实线,除了 1。
如果我们使用区间表示法,我们可以写成 \(Range(f) = (-\infty, 1) \cup (1, +\infty)\)。
例2
求函数 \(f(x) = x^2 - 4x + 3\) 的范围:
回答:
同样,我们继续使用代数方法,所以你知道练习:让 \(y\) 是一个数字,我们将在以下等式中求解 \(x\):\(f(x) = y\)。如果 \(f(x) = y\) 可以求解 \(x\),则 \(y\) 值在范围内。
在这种情况下,我们有:
\[\large f(x) = y \Leftrightarrow x^2 - 4x + 3 = y\] \[\Rightarrow \,\,\, x^2 - 4x + 3 - y = 0 \text{ (This is a quadratic equation in x)}\] \[\Rightarrow \displaystyle \,\,\, x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\] \[\Rightarrow \displaystyle \,\,\, x = \frac{-(-4) \pm \sqrt{(-4)^2 - 4(1)(3-y)}}{2(1)}\] \[\Rightarrow \displaystyle \,\,\, x = \frac{4 \pm \sqrt{16 - 4(3-y)}}{2}\] \[\Rightarrow \displaystyle \,\,\, x = \frac{4 \pm \sqrt{16 - 12 + 4y}}{2}\] \[\Rightarrow \displaystyle \,\,\, x = \frac{4 \pm \sqrt{4 + 4y}}{2}\] \[\Rightarrow \displaystyle \,\,\, x = 2 \pm \sqrt{1+y}\]现在,看到这个最后的表达式, \(x\) 什么时候会被明确定义?我们需要让平方根的参数必须是非负的,所以我们需要:
\[1+y \ge 0\]这意味着 \(y \ge -1\)。如果我们使用区间表示法,我们可以写 \(Range(f) = [-1, +\infty)\)。
在这个例子中,我们可以使用 \(f(x) = x^2 - 4x + 3\) 是一个二次函数,并且它的图形是一个向上开口的抛物线这一事实来解决它。
该抛物线的极小点在顶点处达到。顶点的 x 坐标为:
\[\displaystyle x_V = \frac{-b}{2a} =\frac{-(-4)}{2(1)} =\frac{4}{2} = 2\]现在,只需将值 \(x_V = 2\) 代入二次函数即可找到顶点的 y 坐标:
\[y_V = f(x_V) = 2^2 - 4(2) + 3 = -1\]由于抛物线所达到的最小值是\(-1\),我们得出的范围是\([-1, +\infty)\),这与代数求得的结论相同。
函数 \(f(x) = x^2 - 4x + 3\) 的图形使它更加清晰:
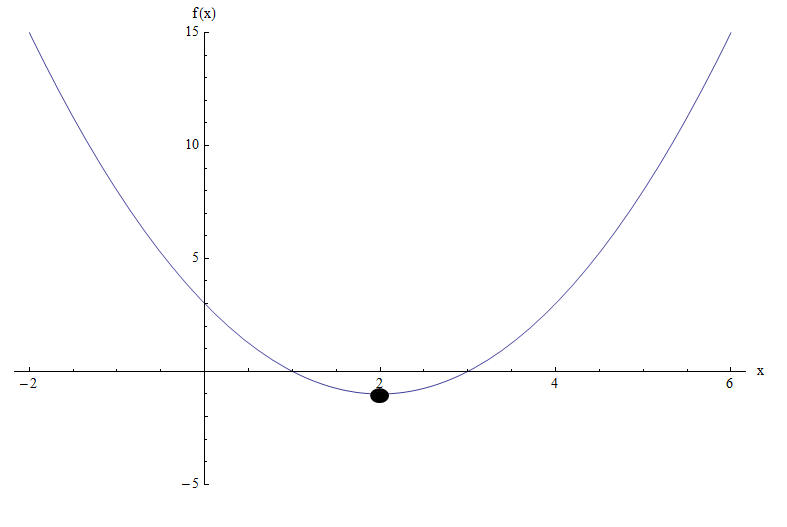
我们可以看到,根据该图,最小值在 \(x = 2\) 处达到,这正是在顶点 x 坐标处找到的值。
使用图形来查找范围的风险在于,您可能会误读图形中的临界点,并对函数达到最大值或最小值的位置给出不准确的评估。
查找函数范围的其他策略
正如我们在前面的例子中看到的,有时我们可以通过查看它的图形来找到函数的范围。
例如,假设您要查找函数 \(f(x) = x + 3\) 的范围。图表如下所示:
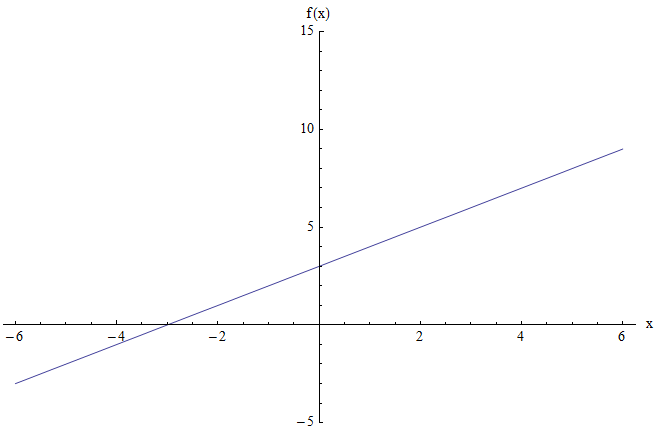
上图未显示任何最小值或最大值。而且,当 \(x\) 大且为正时,函数的值也大且为正。类似地,当 \(x\) 非常负时,函数的值也非常负。
直觉是,通过选择足够大(正或负)的 \(x\) 值,函数可以根据我们想要的值取负值和正值。然后,结论是范围是整条实线,即使用区间表示法的 \((-\infty, +\infty)\)。
这种分析从结果上看是正确的,但从推理上看却是站不住脚的。查找范围的“图形方法”存在这个问题:从直观的角度来看它很有吸引力,但在内容方面却相当薄弱。
通常,如果可能,我们应该更喜欢分析/代数方式。在示例中,我们需要求解 \(x\):
\[x + 3 = y\] \[\Rightarrow \,\, x = y - 3\]那么,对于要明确定义的 \(x\) 是否对 \(y\) 有任何限制?完全没有,因此,对 \(y\) 没有限制,结论是范围是整条实线。
你可以查看你想看的这篇文章 知道如何找到函数的域 反而。
找到范围有很多很好的代数理由,其中之一是因为它是 求函数的逆 .
