学习如何找到函数的域是代数中的一项关键技能,因为它使您能够评估函数的正确定义位置。或者换言之,可以操作该功能的区域

找到操作函数的有效位置的任务是一项有用的任务。例如,考虑函数 \(f(x) = \sqrt x\)。我们知道该函数操作值使得 \(x \ge 0\)。我们不能处理负数,因为我们会得到类似 \(f(-1) = \sqrt{-1}\) 的东西,它没有明确定义（至少作为实数）

您可以查看我们之前的教程,我们在其中深入讨论了 域和范围 .本教程将面向查找域的操作部分。

为什么我们需要找到域？

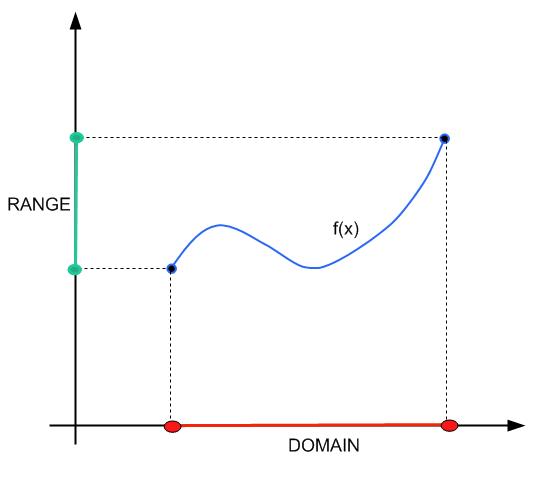
我们需要找到函数域的原因是每个函数在定义它的地方都有一组特定的值。并非所有函数都在实数行中的任何地方定义。

域 实线中的区域 有效的 与函数 \(f(x)\) 一起使用,就 \(x\) 可以采用的值而言。

我们需要做什么才能找到域？

真的,没有一种技巧适合所有尺寸。每个函数都是不同的,需要使用不同的策略来查找域,具体取决于函数。

您始终需要考虑两种技术：

技巧一 : 确保除以零。

此外,那些导致除以零的点需要从域中排除。

技巧二 ：确保存在带有负参数的除法平方根（如 \(\sqrt{-1}\)）。

此外,那些导致负数平方根的点需要从域中排除。

最终,使用这两种技术,您应该能够清除不在域中的点。实线中的其余点只是域的一部分。

因此,这两种技术解决了知道如何代数地找到函数域的问题。另一种方法是查看图表（如果有）。

例 1

找到函数 \(f(x) = \sqrt{x+4}+3\) 的域

回答：

我们需要做的第一件事,也是我们找到域的成功所在,是确定我们可能在哪里找到无效的操作,例如除以零或负平方根。

对于函数 \(f(x) = \sqrt{x+4}+3\),没有潜在的零除,但有一个平方根。为了有有效的参数,平方根内的参数必须是非负的。

因此,为了使 \(x\) 在函数的域中,我们需要有 \(x\ge 0\)。这意味着 \(f\) 的域是 \(\{x: x\ge 0\}\),如果我们使用区间表示法,则是 \([0, +\infty)\)。

总是那么容易吗？？不是真的,它可以变得尽可能困难,这取决于函数 \(f(x)\) 的复杂性。

但是,通常情况下,您在测试和作业中看到的示例相当简单。让我们在难度方面再上一个台阶。

例2

现在找到函数 \(\displaystyle f(x) = \sqrt{\frac{x+4}{x-3}}\) 的域

回答：

这个函数有点复杂,需要更仔细的处理。在这种情况下,我们需要担心被零除法和负平方根的可能除法。

首先,当 \(x = 3\) 时可能会被零除,这表明 \(x = 3\) 应该从域中排除。

现在,我们需要处理潜在的负平方根。我们需要评估 \(\displaystyle \frac{x+4}{x-3}\) 的符号。此外,我们需要它是非负的,所以我们需要解决：

为了使除法为非负,我们需要分子和分母都为正,或者分子和分母都为负。

换句话说,我们需要 \(x+4 \ge 0\) 和 \(x-3 > 0\),或者 \(x+4 \le 0\) 和 \(x-3 < 0\)。

这与 \(x \ge -4\) 和 \(x > 3\) 或 \(x \le -4\) 和 \(x < 3\) 相同。

这可以写成 \(x > 3\),或者两者都写成 \(x \le -4\),它对应于区间 \( (-\infty, -4] \cup (3, +\infty)\)。

结论是函数 \(\displaystyle f(x) = \sqrt{\frac{x+4}{x-3}}\) 的定义域是：

如您所见,难度级别有所增加,您实际上可以根据需要增加难度。

如何找到有理函数的域

首先,让我们回想一下有理函数是两个多项式的商,形式为：

你如何找到上述有理函数的域？我们需要遵循我们的规则：通过零和负平方根寻找潜在的除法。

在这种情况下,不存在潜在的负平方根,但可以被零除,只要分母中的多项式为零。

结论很简单：有理函数的域是整条实线,除了那些分母多项式为零的点。

例3

查找域

回答：

首先,我们需要明白这是一个有理函数,因为分子和分母中分别有两个多项式\(p(x) = x^2 + x + 1\) 和\(q(x) = x^3 - 6x^2 + 11x - 6\)。

那么,第一步就是在分母中找到多项式的零点,所以我们需要求解：\[ x^3 - 6x^2 + 11x - 6 = 0\]

这个方程有点难解,所以我会告诉你确实是 \(x^3 - 6x^2 + 11x - 6 = (x-1)(x-2)(x-3)\),所以我们需要解决：

这意味着分母中多项式的根是\(x_1 = 1, x_2 = 2, x_3 = 3\)。结论是该函数的域是整条实线,除了点 1,2 和 3。使用区间表示法,域是 \((-\infty, +\infty) \backslash \{1,2,3\}\)。

查找函数域的其他策略

通过查看零或负平方根的潜在除法来查找函数域的替代方法（这是一种分析方法）是查看图形。

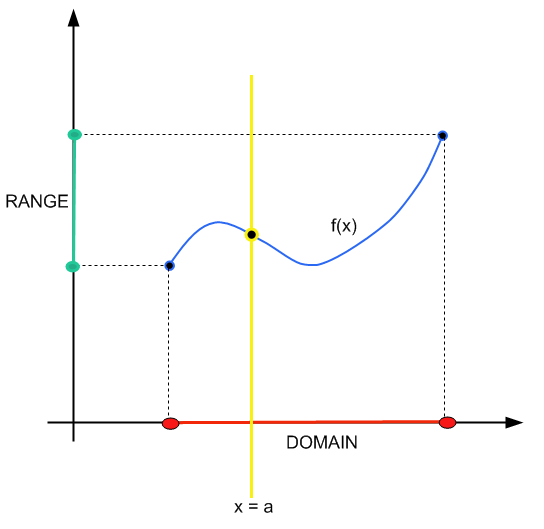
方法很简单：你构造一条垂直线\(x = a\)。如果该垂直线在一个且仅一个点与函数图相交,则 \(x = a\) 属于域。

简短而甜蜜。

最后,你如何找到一个具有平方根的函数的域

这是我们一直在谈论的其中一项技术的核心,即寻找潜在的负平方根。那么,当您有一个具有一个或多个平方根的函数时,您就知道很可能有一个潜在的负根,您需要检测它。

然而,情况并非总是如此。想想函数 \(f(x) = \sqrt{x^2}\)。该函数有一个平方根,但里面的参数是\(x^2\),它不能为负,所以我们有一个函数的平方根没有负平方根的情况。