如何分解
学习如何分解是您可以学习的最重要的技能之一。保理有如此多的应用,您会很高兴花时间了解它的所有内容。
因式分解通常是我们认为理所当然的事情,并且基于不同的属性,例如可交换的,结合的和分配的属性。这些属性允许您以方便的方式移动和分组术语。
关于交换,结合和分配属性的快速更新。对于实数 \(x\),\(y\) 和 \(z\),我们有以下性质
（加法的结合性）\((x+y)+z = x+(y+z)\)
加法的交换性）\( x + y = y + x\)
（分配属性）\( x \cdot (y+z) = x \cdot y + x \cdot z\)
其中 \(+\) 和 \(\cdot\) 分别是实数的和和乘积。
为什么知道如何分解是有用的？
原因有很多,但其中一个关键的原因是因式分解为我们提供了一种求解方程的简单方法。事实上,因式分解是我们解方程的方法。
例如,考虑我们试图求解 \(x\) 的方程：
\[\large xy +xz = 0\]我们该怎么做？那么,我们可以使用分配属性得到：
\[\large x y + x z = x(y+z) = 0\]因此,在最后一个表达式 \( x(y+z) = 0\) 中,我们有一个因式分解的例子。实际上,我们采用了初始表达式 \(xy+xz\) 并将其分解为 \( x(y+z)\)。
所以,现在我们需要求解一个更简单的方程,即 \( x(y+z) = 0\)。为什么更容易？这是因为现在我们知道乘积 \( x(y+z)\) 等于零,那么因子之一需要等于零。
所以,如果我们知道 \(y+z = \not 0\),那么我们就知道我们需要有那个 \(x = 0\)。
课
：因式分解的一个优点是能够将方程写为等于零的因子的乘法。那么,至少有一个因素必须为零。
例如,当我们需要在以下等式中求解 \(x\) 时：
\[\large 5x + 3x = 0\]当我们这样做时,我们没有意识到我们实际上是在考虑因素
\[\large 5x + 3x = (5+3)x = 8x = 0\]所以我们将方程简化为等于零的因子乘积：\(8x = 0\)。由于 \(8\) 因素之一不等于零,因此唯一可能的解决方案是 \(x = 0\)。
换句话说
: 如果你知道如何分解,你可能会知道
如何解方程
.
如何分解多项式
就解方程的有用性而言,因式分解的作用现在应该很清楚了。唯一的问题是没有一个通用的单一策略可以用来分解所有可能的代数表达式。
所以,通常情况下,我们很乐意分解相对简单的表达式,但理想情况下,我们想知道如何分解尽可能多的表达式。
平衡是通过一类非常通用的表达式来实现的,我们通常可以非常系统地考虑这些表达式。该类是多项式类。例如,表达式
\[\large 2x^2 + 5x + 3\]是 2 次多项式。 或者下面的表达式
\[\large x^3 - 3x^2 + 4x+2\]是 3 次多项式。
一般来说,形式的表达
\[\large a_n x^n + a_{n-1}x^{n-1} + ... + a_1 x + a_0\]是 \(n\) 次多项式。自然,表达式越简单,化简就越容易,所以我们应该先尝试学习如何对二次表达式进行因式分解。这就是二阶多项式。
例 1
分解以下二次表达式
\[\large x^2 + x - 2\]回答：
这个例子将故意向您展示,即使是最简单的表达式,如上面的表达式,也可能很难分解。你会怎么做？
如果我告诉你,你需要加零怎么办？这有点可笑,对吧？让我们来看看：
\[\large x^2 + x - 2 = x^2 + x + 0 - 2 \]你同意上面的说法吗？我刚刚添加了 \(0\)。什么也没有变。但是,如果我告诉你 \(0 = 2x - 2x\) 呢？那么
\[\large x^2 + x - 2 = x^2 + x + 0 - 2 = x^2 + x + (2x - 2x) - 2 \]全部都一样！它有效,因为我添加了零,所以没有任何变化。但是现在我们将其展开并分组：
\[\large x^2 + x - 2 = x^2 + x + 0 - 2 \] \[\large = x^2 + x + (2x - 2x) - 2 \] \[ \large = x^2 + x - 2x + 2x - 2 \] \[\large = x^2 + (x - 2x) + 2x - 2 \] \[\large = x^2 - x + 2x - 2 \] \[\large = x(x-1) + 2(x-1)\] \[\large = (x+2)(x-1)\]那么,最后,\(x^2 + x - 2 = (x+2)(x-1)\)。棘手？也许吧,但这是一种方法。尽管这是一种聪明的方法,但我们更喜欢更系统的方法。
分解二次多项式
聪明的技巧很好,所有这些,但通常我们会更喜欢一种系统的方法,它永远不会失败。对于二次多项式（2 次多项式）,有一种进行因式分解的系统方法：
第1步
：给定二次表达式\(ax^2 + bx + c\),我们首先解方程
第2步
：如果上述方程的解（根）是实数（即使只有一个根）,我们称这些根为 \(x_1\) 和 \(x_2\)。有了这些根,我们得到以下因素：
所以解 \(x_1\) 和 \(x_2\) 完全确定了因素。
自然在这种情况下,正如预期的那样,求解二次方程与分解二次方程密切相关。
例2
分解以下二次方程
\[\large x^2 - 4x + 3\]通过计算其根。
回答：
我们从求解相应的二次方程开始：
\[\large x^2 - 4x + 3 = 0\]使用著名的和众所周知的 二级公式 ：
\[\large\displaystyle x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \] \[\large\displaystyle = \frac{-(-4) \pm \sqrt{(-4)^2 - 4(1)(3)}}{2(1)} \] \[\large\displaystyle = \frac{4 \pm \sqrt{16 - 12}}{2} \] \[\large\displaystyle = \frac{4 \pm \sqrt{4}}{2} \] \[\large\displaystyle = \frac{4 \pm 2}{2} \]这意味着解（根）是 \(x_1 = 1\) 和 \(x_2 = 1\)。然后,二次表达式 \(x^2 - 4x + 3\) 可以分解如下：
\[\large x^2 - 4x + 3 = a(x - x_1)(x - x_2) = (x-1)(x-3) \]请注意,在这种情况下,与 \(x^2\) 项相乘的项是 1,因此在这种情况下是 \(a = 1\)。
阶数大于 2 的因式分解多项式
因此,要分解二次多项式,我只需计算相应二次方程的根。我如何分解更高阶的多项式？ 使用完全相同的方法 .
第1步：
给定多项式表达式 \(a_n x^n + a_{n-1}x^{n-1} + ... + a_1 x + a_0\),我们首先解方程
\[\large a_n x^n + a_{n-1}x^{n-1} + ... + a_1 x + a_0 = 0\]
第2步：
如果上述方程的解（根）是实数（即使它们重复）,我们称这些根为 \(x_1\),\(x_2\),...,\(x_n\)。有了这些根,我们得到以下因素：
\[\large a_n x^n + a_{n-1}x^{n-1} + ... + a_1 x + a_0 = a_n(x - x_1)(x - x_2)\cdots (x - x_n)\]
因此,似乎对 2 次多项式进行因式分解与对 10 次多项式进行因式分解一样简单。理论上,答案是肯定的。
唯一的问题是没有一个简单的封闭代数公式可以求解 5 次或更高阶多项式方程的根。
有时,我们可以通过查看图表,甚至使用计算器来求解更高阶的方程。例如,检查下图：
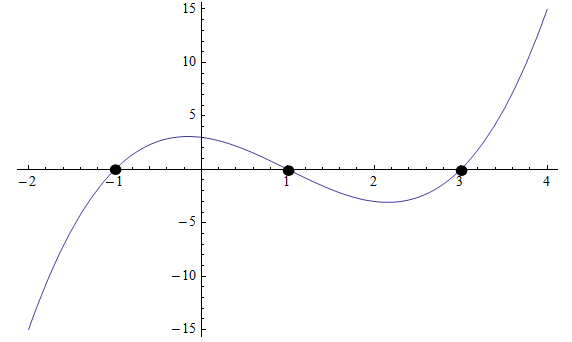
从图形上看,我们可以看到多项式在三个点与 x 轴交叉：\(x_1 = -1\),\(x_2 = 1\) 和 \(x_3 = 3\),因此这些是根。
那么,我们知道多项式必须是 \(p(x) = a(x+1)(x-1)(x-3)\) 形式。我们还需要知道一点才能知道常量 \(a\)。
更多关于保理
我们只是用因式分解的概念触及皮毛,尽管对于一般表达式可以做的并不多。我们能做的最好的事情就是对因子多项式给出一个系统的方法。
但是,对因式多项式进行一般处理并不是一件小事,使用根来因式多项式的想法无异于代数基本定理。所以,至少通过标题,你可以看出它并不小。
分解一般表达式
没有一般规则可以分解一般表达式。我们需要靠耳朵玩耍并尝试利用表达式的结构。有时我们可以考虑因素,有时我们不能。这一切都取决于表达。唯一的一般规则是尝试分组并尝试找到共同因素,以便进一步分组和简化。
如何通过分组进行分解
这是我们做的第一个例子。说你有：
\[\large x^2 - x + 2x - 2 \]所以我们将前两项和后两项分组以获得：
\[\large (x^2 - x) + (2x - 2) \]并且这些组中的每一个都可以被分解为
\[\large x(x - 1) + 2(x - 1) \]现在我们有两个具有公因数 \(x-1\) 的项,因此我们将其分解为
\[\large (x+2)(x - 1) \]有时使用计算器来计算因子更实用。您可以使用我们的 二次方程求解器 求二次表达式的因数。
请注意,当您需要分解表达式时,有几种技术可以帮助您,具体取决于其结构。其中之一是方法 分组因素 当它起作用时,可以大大简化简化过程。