代数教程

求解对数方程

解决对数方程式是您在处理代数程序时必须做的事情,值得开发一个具体的战略来处理它们。

在本教程中您将学习的是您需要遵循的主要策略来解决对数方程。

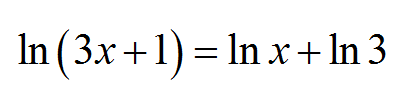
什么是对数方程式？

我们需要的第一件事是定义对数方程是什么。

对数等式是涉及至少一个未知变量的等式,其中对数表达式出现在等式的至少一侧 。

对数方程的一个例子是

\[\ln x = 2\ln x - \ln 3\]

或者

\[ \ln(3x-1) - \ln(2x + 1) = 1\]

请注意,对数方程可以包含多个未知,例如

\[ \ln(x-1) = \ln(2y + 1)\]

求解对数方程的策略

第一个免责声明是没有防弹方法来解决对数方程,也没有概述这一事件的一般方程。这就是所有方法的原因在等式中假设某些结构,这在所有方程中不一定存在。

因此,我们无法找到解决对数方程的方式,因为没有一种方式可以处理所有可能的情况。

尽管如此,还有几种策略将为您提供最佳机会,并找到解决方案,如果存在。

首先,尝试将所有对数表达式分组为一个对数表达式。

这通常通过使用最常见的方式实现日志规则如果表达式的结构允许,则允许您紧凑地表达对数表达式。

其次,一旦尽可能地压缩了对数表达式,您将通过通常将指数函数应用于平等的两侧来摆脱它们。

最后一步,希望将从图片中删除所有对数,并且它将允许您为未知来解决。

因此,换句话说,求解对数方程包括分组对数表达式,通过应用指数来消除它们,然后将等式作为常规方程求解。

显然,当你摆脱了对数的时候,你面临一个可以拥有自己挑战的等式。

解决对数方程的不同示例

没有更好的学习如何解决方程而不是实际练习解决它们：

例1：

解决以下等式：

\[\large 4 \log(\sqrt x) = \log(6x-1)\]

回答：

让我们遵循战略。该想法是尽可能地紧凑的对数表达式。这是一个判断呼叫,因为主要的想法是基本上摆脱了对数。

使用日志规则我们可以将“4”放在对数的内部

\[\large 4 \log(\sqrt x) = \log(6x-1)\] \[\large \Rightarrow \log((\sqrt x)^4) = \log(6x-1)\] \[\large \Rightarrow \log(x^2) = \log(6x-1)\]

现在,对数表达式尽可能压缩,我们需要摆脱对数。

这样做的一种方法是将指数函数\(10^x\)应用于平等的每一侧。我的意思是什么???

好吧,你有双方的平等。由于双方都是相同的,当用作函数的参数\(10^x\)时,它应该保持平等。所以我们有

\[\large \log(x^2) = \log(6x-1)\] \[\large \Rightarrow 10^{\log(x^2)} = 10^{\log(6x-1)}\] \[\large \Rightarrow x^2 = 6x-1\]

因为我们知道\(10^{\log a} = a\),它是基本日志规则之一。

所以现在我们已经消除了对数的,我们可以解决剩下的等式：

\[\large x^2 = 6x-1\] \[\large \Rightarrow x^2 - 6x + 1 = 0\] \[\large \Rightarrow x = \frac{-(-6) \pm \sqrt{(-6)^2-4(1)(1)}}{2(1)}\] \[\large \Rightarrow x = \frac{6 \pm \sqrt{36-4}}{2}\] \[\large \Rightarrow x = \frac{6 \pm \sqrt{32}}{2}\] \[\large \Rightarrow x = \frac{6 \pm 4\sqrt{2}}{2}\] \[\large \Rightarrow x = 3 \pm 2\sqrt 2\]

所以那么\(x_1 = 3 + 2\sqrt 2\)和\(x_2 = 3 - 2\sqrt 2\)。从技术上讲,您需要检查这两个是否是原始方程的解决方案,以确保它们属于对数表达式的域。

在这种情况下,\(x_1 = 3 + 2\sqrt 2\)和\(x_2 = 3 - 2\sqrt 2\)是原始方程的解决方案。

例2：

解决以下对数方程：

\[\large \ln 5 - \ln(6-x) = \ln x\]

回答：

使用日志规则我们可以压缩日志表达式,我们得到了

\[\large \ln 5 - \ln(6-x) = \ln x\] \[\large \displaystyle \Rightarrow \ln\left(\frac{5}{6-x}\right) = \ln x\] \[\large \displaystyle \Rightarrow e^{\ln\left(\frac{5}{6-x}\right)} = e^{\ln x}\] \[\large \displaystyle \Rightarrow \frac{5}{6-x} = x\]

因为我们知道\(e^{\ln a} = a\),它是基本日志规则之一。

因此,现在我们已经消除了对数,我们可以解决我们离开的等式：

\[\large \displaystyle \frac{5}{6-x} = x\] \[\large \displaystyle \Rightarrow 5 = x(6-x)\] \[\large \displaystyle \Rightarrow 5 = 6x - x^2\] \[\large \displaystyle \Rightarrow x^2 -6x + 5 = 0\] \[\large \displaystyle \Rightarrow (x-1)(x-5) = 0\]

所以那么\(x_1 = 1\)和\(x_2 = 5\)。让我们将这些值插入原始方程,以查看它们是否实际上解决方案：

对于\(x_1 = 1\)：

\[\large \ln 5 - \ln(6-1) = \ln 1\]

这与：

\[\large \ln 5 - \ln(5) = 0\]

这是真的,所以等式持有。

对于\(x_1 = 5\)：

\[\large \ln 5 - \ln(6-5) = \ln 5\]

这与：

\[\large \ln 5 - \ln(1) = \ln(5)\]

这是真的,所以等式持有。

因此,对等式的解决方案是\(x_1 = 1\)和\(x_2 = 5\)。