表格的弧弹性公式

需求弧弹性公式允许您估计需求计划表中给定点的弹性,而无需需求函数的明确公式。

您需要提供的是一张表格,其中一栏为价格,一栏为需求量。在提供的电子表格中输入或粘贴该表格后,您将单击"计算"以计算相应的弧弹性。

请注意,这只是一个近似值：理想的情况是 使用需求函数计算弹性 通过使用导数。

对表使用弧弹性的步骤

这 弧弹性公式 是。

\[ \varepsilon_{ARC} = \displaystyle \left(\frac{Q_2 - Q_1}{P_2 - P_1}\right) \left(\frac{P_1 + P_2}{Q_1 + Q_2}\right)\]

这可以应用于需求计划表中的连续点。您将遵循以下步骤：

• 步骤1： 正确列出价格（P）和需求量（Q）的值
• 第2步： 如果要使计算更清晰,您可以创建 Q2 - Q1,P2 - P1,Q1 + Q2 和 P1 + P2 的列,或者直接计算公式
• 第3步： 表中将有一个跳过的点,因为弧弹性取表上的一个点和表中紧随其后的点

使用这种弧弹性近似值将为您提供对正在分析的特定商品的价格变化敏感度的绝佳图像,即使它只是近似值。

需求点越多,近似值就越好,特别是当这些价格点接近时。

弧弹性测量什么？

弧弹性旨在提供给定点真实弹性的近似值。需求曲线的实际弹性通过以下公式计算：

\[ \varepsilon = \displaystyle \frac{dQ}{dP} \cdot \frac{P}{Q}\]

有人可能会说弧弹性只是一种近似值,那么它怎么会有价值呢？答案是,对于弹性分析以及一般经济学中的敏感性分析,我们更感兴趣的是范围,而不是非常具体的点。

事实上,对于微观经济学而言,了解我们是否处于无弹性范围是有用的,而不是了解弹性的具体值

并不是说具体值不重要,因为有它确实是件好事,但是弧弹性通常是一个很好的近似值,它们可以非常精确地表示我们所面临的弹性范围类型。

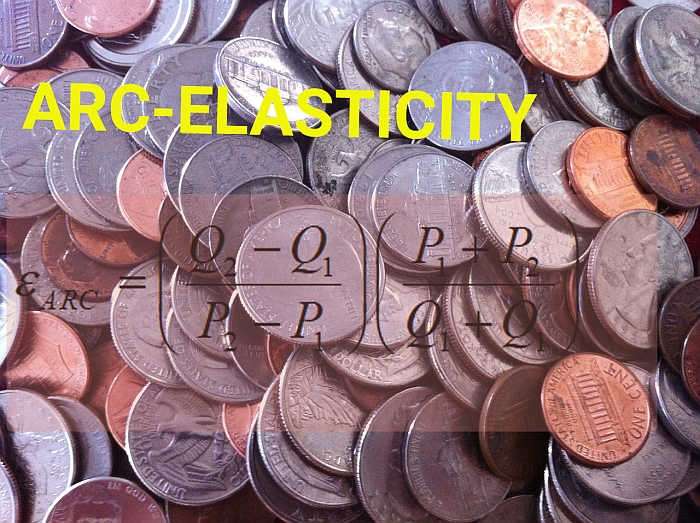
例子

考虑以下需求表,其中包含有关价格和需求量的信息

提供此表中数据点的弧弹性近似值。

磷	问
1	200
1.5	190
2	170
2.5	155
3	130
3.5	110
4	90
4.5	60

解决方案： 为了从这些数据中近似计算需求价格弹性,我们需要使用以下弧弹性公式

\[ \varepsilon_{ARC} = \displaystyle \left(\frac{Q_2 - Q1}{P2_P1}\right)\left(\frac{P_1 + P_2}{Q_1 + Q_2}\right)\]

通过将上述公式应用于所有连续数据点对,我们发现以下弧弹性：

磷	问	弧弹性
1	200	-
1.5	190	\(\left(\frac{ 190 - 200}{ 1.5 - 1}\right) \left(\frac{ 1 + 1.5}{ 200 + 190}\right) = -0.13\)
2	170	\(\left(\frac{ 170 - 190}{ 2 - 1.5}\right) \left(\frac{ 1.5 + 2}{ 190 + 170}\right) = -0.39\)
2.5	155	\(\left(\frac{ 155 - 170}{ 2.5 - 2}\right) \left(\frac{ 2 + 2.5}{ 170 + 155}\right) = -0.42\)
3	130	\(\left(\frac{ 130 - 155}{ 3 - 2.5}\right) \left(\frac{ 2.5 + 3}{ 155 + 130}\right) = -0.96\)
3.5	110	\(\left(\frac{ 110 - 130}{ 3.5 - 3}\right) \left(\frac{ 3 + 3.5}{ 130 + 110}\right) = -1.08\)
4	90	\(\left(\frac{ 90 - 110}{ 4 - 3.5}\right) \left(\frac{ 3.5 + 4}{ 110 + 90}\right) = -1.5\)
4.5	60	\(\left(\frac{ 60 - 90}{ 4.5 - 4}\right) \left(\frac{ 4 + 4.5}{ 90 + 60}\right) = -3.4\)

解释

下表显示了每个价格点的近似需求价格弹性。这些值可以大致用于确定所提供需求计划的弹性和非弹性范围。

其他经济计算器

如果你从事计量经济学工作,这 回归计算器 可能会很有用,特别是因为它展示了 回归系数的计算 .

您还可以使用 对数对数方程 估计 恒定弹性需求曲线 .