Умение учитывать фактор - один из важнейших навыков, которым вы можете научиться. У факторинга так много приложений, что вы будете рады потратить время, чтобы узнать о нем все, что есть.

Коротко о свойствах коммутативности, ассоциативности и распределения. Для действительных чисел \(x\), \(y\) и \(z\) у нас есть следующие свойства

(Ассоциативность сложения) \((x+y)+z = x+(y+z)\)

Коммутативность сложения) \( x + y = y + x\)

(Распределительная собственность) \( x \cdot (y+z) = x \cdot y + x \cdot z\)

где \(+\) и \(\cdot\) - сумма и произведение действительных чисел соответственно.

Почему полезно знать, как учитывать факторы?

Причин много, но одна из важнейших состоит в том, что разложение на множители дает нам простой способ решения уравнений. Фактически, факторинг - это ТОЧНЫЙ способ решения уравнений.

Например, рассмотрим уравнение, в котором мы пытаемся решить для \(x\):

Как мы это делаем? Что ж, мы можем использовать свойство distributive, чтобы получить:

Следовательно, с этим последним выражением \( x(y+z) = 0\) у нас есть пример факторинга. Действительно, мы взяли исходное выражение \(xy+xz\) и разложили его на \( x(y+z)\).

Итак, теперь нам нужно решить более простое уравнение \( x(y+z) = 0\). Почему так проще? Это потому, что теперь, когда мы знаем, что произведение \( x(y+z)\) равно нулю, тогда один из факторов НЕОБХОДИМО равняться нулю.

Итак, если мы знаем, что \(y+z = \not 0\), тогда мы знаем, что нам нужен этот \(x = 0\).

УРОК : Одним из преимуществ факторинга является возможность написать уравнение как произведение множителей, равное нулю. Тогда, ПО крайней мере, ОДИН ИЗ ФАКТОРОВ ДОЛЖЕН БЫТЬ НУЛЕМ.

Например, когда нам нужно найти \(x\) в следующем уравнении:

мы не осознаем, что на самом деле производим факторинг, когда делаем

поэтому мы свели наше уравнение к произведению факторов, равному нулю: \(8x = 0\). Поскольку один из факторов \(8\) не равен нулю, единственно возможное решение - \(x = 0\).

Другими словами : если вы знаете, как фактор, вы, вероятно, будете знать как решать уравнения .

Как разложить многочлены на множители

Баланс достигается с помощью очень общего класса выражений, который мы можем зачастую очень систематически учитывать. Этот класс - класс многочленов. Например, выражение

является многочленом степени 2. Или приведенное ниже выражение

- многочлен степени 3.

В общем, выражение вида

является многочленом степени \(n\). Естественно, чем проще выражение, тем легче его будет упростить, поэтому сначала мы должны попытаться научиться разложить квадратные выражения на множители. Это полиномы второй степени.

ПРИМЕР 1

Разложите на множители следующее квадратное выражение

ОТВЕЧАТЬ:

Этот пример специально покажет вам, что может быть сложно разложить на множители даже самое простое выражение, подобное приведенному выше. Что бы вы сделали, чтобы это учесть?

Что, если я скажу вам, что вам нужно добавить ноль? Это просто смешно, правда? Давайте посмотрим:

Вы согласны с вышеизложенным? Я только что добавил \(0\). Ничего не изменилось. Но что, если я скажу вам, что \(0 = 2x - 2x\)? Итак, тогда

Все так же! Работает, потому что я добавил ноль, поэтому ничего не меняется. Но теперь мы расширяем его и группируем:

Итак, наконец, \(x^2 + x - 2 = (x+2)(x-1)\). Сложный? Возможно, но это один из способов сделать это. Несмотря на то, что это умный способ сделать это, мы бы предпочли более систематический.

Разложите квадратичный многочлен на множители

Умные трюки - это хорошо, и все такое, но обычно мы предпочитаем систематический подход, который никогда не подводит. Для квадратичных многочленов (многочленов степени 2) существует систематический способ продолжения факторизации:

Шаг 1 : Учитывая квадратное выражение \(ax^2 + bx + c\), мы сначала решаем уравнение

Шаг 2 : Если решения (корни) приведенного выше уравнения действительны (даже если есть только один корень), мы называем эти корни \(x_1\) и \(x_2\). С этими корнями мы получаем следующие факторы:

поэтому решения \(x_1\) и \(x_2\) полностью определяют факторы.

Естественно, что в этом случае, как и следовало ожидать, решение квадратного уравнения тесно связано с факторизацией квадратного уравнения.

ПРИМЕР 2

Разложите на множители следующее квадратное уравнение

вычисляя его корни.

ОТВЕЧАТЬ:

Начнем с решения соответствующего квадратного уравнения:

используя известные и хорошо известные квадратичная формула :

что означает, что решения (корни) - это \(x_1 = 1\) и \(x_2 = 1\). Тогда квадратное выражение \(x^2 - 4x + 3\) можно разложить на множители следующим образом:

Обратите внимание, что в этом случае член умножения члена \(x^2\) равен 1, поэтому в этом случае \(a = 1\).

Факторинг полиномов со степенью больше 2

Итак, чтобы разложить квадратные полиномы на множители, я просто вычисляю корни соответствующего квадратного уравнения. Как разложить на множители многочлены более высокой степени ?? Используя точно такой же метод .

Шаг 1: Учитывая полиномиальное выражение \(a_n x^n + a_{n-1}x^{n-1} + ... + a_1 x + a_0\), мы сначала решаем уравнение

Шаг 2: Если решения (корни) приведенного выше уравнения действительны (даже если они повторяются), мы называем эти корни \(x_1\), \(x_2\), ..., \(x_n\). С этими корнями мы получаем следующие факторы:

Таким образом, может показаться, что разложить на множители многочлен степени 2 так же просто, как разложить на множители многочлен степени 10. Теоретически ответ - да.

Единственная проблема заключается в том, что не существует простой близкой алгебраической формулы, которая могла бы найти корни для полиномиального уравнения степени 5 или выше.

Иногда мы можем решить уравнения более высокой степени, глядя на график или даже используя калькулятор. Например, посмотрите график ниже:

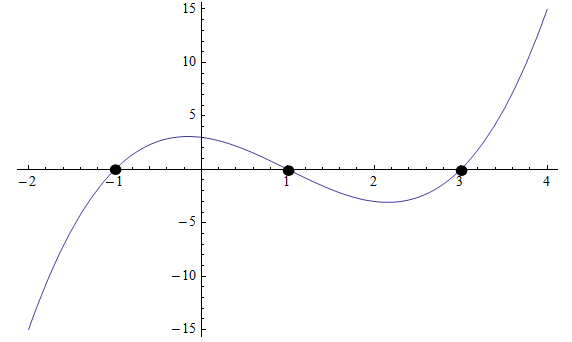
Графически мы можем видеть, что многочлен пересекает ось x в трех точках: \(x_1 = -1\), \(x_2 = 1\) и \(x_3 = 3\), так что это корни.

Итак, мы знаем, что многочлен должен иметь форму \(p(x) = a(x+1)(x-1)(x-3)\). Нам нужно знать еще один момент, чтобы узнать константу \(a\).