Как найти домен
Умение находить область определения функции - важный навык в алгебре, потому что он дает вам возможность оценить, где функция определена правильно. Или, другими словами, регион, в котором допустимо использовать функцию
Задача найти, где допустимо использовать функцию, является полезной. Например, рассмотрим функцию \(f(x) = \sqrt x\). Мы знаем, что функция оперирует такими значениями, что \(x \ge 0\). Мы не можем работать с отрицательными числами, потому что мы получили бы что-то вроде \(f(-1) = \sqrt{-1}\), что не совсем точно (по крайней мере, как действительное число)
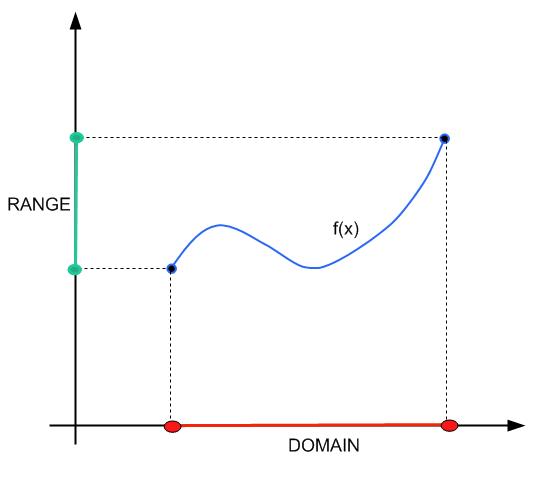
Вы можете проверить наш предыдущий урок, в котором мы подробно говорили о домен и диапазон . Это руководство будет ориентировано на оперативную часть поиска домена.
Зачем нам нужно искать домен?
Причина, по которой нам нужно найти область определения функции, заключается в том, что каждая функция имеет определенный набор значений, в которых она определена. Не все функции определены везде в реальной строке.
Домен, область на реальной линии, где он находится действительный для работы с функцией \(f(x)\) в терминах значений, которые может принимать \(x\).
Что нам нужно сделать, чтобы найти домен?
На самом деле не существует одной хитрости, подходящей для всех размеров. Каждая функция отличается, и для поиска области необходимо использовать разные стратегии в зависимости от функции.
Вы ВСЕГДА должны учитывать два метода:
Техника 1.
: Убедитесь, что есть деления на ноль.
Причем те точки, которые приводят к делению на ноль, нужно исключить из области.
Техника 2.
: Убедитесь, что есть квадратные корни делений с отрицательными аргументами (например, \(\sqrt{-1}\)).
Более того, те точки, которые приводят к извлечению квадратного корня из отрицательного числа, необходимо исключить из домена.
В конечном итоге, используя эти два метода, вы сможете отсеять точки, которых нет в домене. Остальные точки на реальной линии просто ЯВЛЯЮТСЯ частью домена.
Итак, эти два метода решают проблему знания того, как найти область определения функции алгебраически. Другой способ сделать это - посмотреть на график, если он доступен.
ПРИМЕР 1
Найдите домен функции \(f(x) = \sqrt{x+4}+3\)
ОТВЕЧАТЬ:
Первое, что нам нужно сделать, и именно в этом заключается наш успех в поиске домена, - это определить, где потенциально мы могли бы найти недопустимые операции, такие как деление на ноль или отрицательные квадратные корни.
Для функции \(f(x) = \sqrt{x+4}+3\) нет потенциальных делений на ноль, но есть квадратный корень. Чтобы иметь действительный аргумент, аргумент внутри квадратного корня должен быть неотрицательным.
Следовательно, чтобы \(x\) находилось в домене функции, нам нужно иметь \(x\ge 0\). Это означает, что домен \(f\) - это \(\{x: x\ge 0\}\) или \([0, +\infty)\), если мы используем обозначение интервала.
Всегда ли это просто ?? Не совсем, это может быть так сложно, как вы, в зависимости от сложности функции \(f(x)\).
Однако обычно примеры, которые вы видите в своих тестах и домашних заданиях, довольно просты. Давайте поднимемся на ступеньку выше с точки зрения сложности.
ПРИМЕР 2
Теперь найдите домен функции \(\displaystyle f(x) = \sqrt{\frac{x+4}{x-3}}\)
ОТВЕЧАТЬ:
Эта функция немного сложнее и требует более внимательного отношения. В этом случае нам нужно беспокоиться как о возможных делениях на ноль, так и на отрицательные квадратные корни.
Во-первых, может быть потенциальное деление на ноль, когда \(x = 3\), что указывает на то, что \(x = 3\) следует исключить из домена.
Теперь нам нужно позаботиться о потенциальном отрицательном квадратном корне. Нам нужно оценить признак \(\displaystyle \frac{x+4}{x-3}\). Более того, нам нужно, чтобы он был неотрицательным, поэтому нам нужно решить:
\[\displaystyle \frac{x+4}{x-3} \ge 0\]Чтобы деление было неотрицательным, нам нужно, чтобы числитель и знаменатель были положительными, либо числитель и знаменатель были отрицательными.
Другими словами, нам нужны оба \(x+4 \ge 0\) и \(x-3 > 0\), или оба \(x+4 \le 0\) и \(x-3 < 0\).
Это то же самое, что и \(x \ge -4\), и \(x > 3\), или оба \(x \le -4\) и \(x < 3\).
И это может быть записано как \(x > 3\) или как \(x \le -4\), что соответствует интервалу \( (-\infty, -4] \cup (3, +\infty)\).
Напрашивается вывод, что область определения функции \(\displaystyle f(x) = \sqrt{\frac{x+4}{x-3}}\):
\[ dom(f) = (-\infty, -4] \cup (3, +\infty)\]Как видите, уровень сложности немного увеличился, и вы можете увеличивать его сколько угодно.
Как найти область рациональной функции
Прежде всего, напомним, что рациональная функция - это частное двух многочленов вида:
\[f(x) = \frac{p(x)}{q(x)} = \frac{a_0 + a_1 x + ...+ a_m x^m}{b_0 + b_1 x + ...+ b_n x^n}\]Как найти область для указанной выше рациональной функции? Нам нужно следовать нашему правилу: ищите возможные деления на ноль и отрицательные квадратные корни.
В этом случае нет потенциальных отрицательных квадратных корней, но может быть деление на ноль, если многочлен в знаменателе равен нулю.
Вывод очень простой: область определения рациональной функции - это вся вещественная прямая, ЗА ИСКЛЮЧЕНИЕМ тех точек, в которых многочлен в знаменателе равен нулю.
ПРИМЕР 3
Найдите домен
\[f(x) = \frac{x^2 + x + 1}{x^3 - 6x^2 + 11x - 6}\]ОТВЕЧАТЬ:
Прежде всего, нам нужно понять, что это рациональная функция, потому что у вас есть два полинома \(p(x) = x^2 + x + 1\) и \(q(x) = x^3 - 6x^2 + 11x - 6\) в числителе и знаменателе соответственно.
Итак, первый шаг - найти нули многочлена в знаменателе, поэтому нам нужно решить: \[ x^3 - 6x^2 + 11x - 6 = 0\]
Это уравнение довольно сложно решить, поэтому я дам вам это действительно \(x^3 - 6x^2 + 11x - 6 = (x-1)(x-2)(x-3)\), поэтому нам нужно решить:
\[ x^3 - 6x^2 + 11x - 6 = (x-1)(x-2)(x-3) = 0\]что означает, что корни многочлена в знаменателе равны \(x_1 = 1, x_2 = 2, x_3 = 3\). Вывод состоит в том, что область определения функции - это вся вещественная линия, за исключением точек 1, 2 и 3. При использовании интервальной записи область определения \((-\infty, +\infty) \backslash \{1,2,3\}\).
Другие стратегии поиска области определения функции
Альтернативой поиска области определения функции путем рассмотрения возможных делений на нулевые или отрицательные квадратные корни, что является аналитическим способом, является просмотр графика.
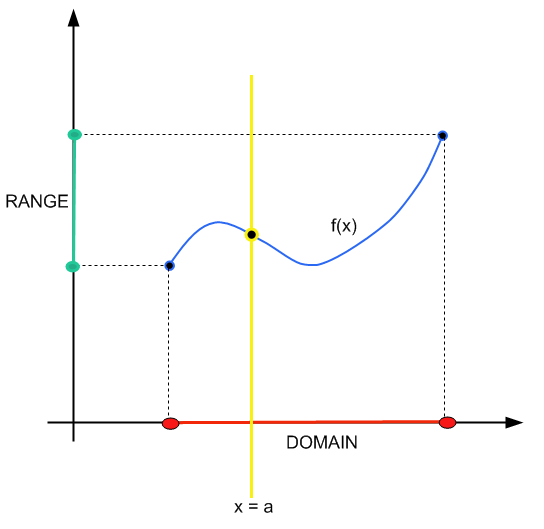
Метод прост: вы строите вертикальную линию \(x = a\). Если эта вертикальная линия пересекает график функции в одной и только одной точке, то \(x = a\) принадлежит домену.
Коротко и мило.
Наконец, как найти область определения функции с квадратным корнем
Это суть одной из техник, о которых мы говорили, а именно нахождения потенциальных отрицательных квадратных корней. Итак, когда у вас есть функция с одним или несколькими квадратными корнями, вы знаете, что очень вероятно, что у вас будет потенциальный отрицательный корень, и вам нужно его обнаружить.
Однако это не всегда так. Подумайте о функции \(f(x) = \sqrt{x^2}\). Эта функция имеет квадратный корень, но аргумент внутри - \(x^2\), который не может быть отрицательным, поэтому мы имеем дело с функцией с квадратным корнем, которая не имеет отрицательных квадратных корней.