Как найти диапазон
Изучение того, как найти диапазон функции, может оказаться очень важным в алгебре и исчислении, потому что это дает вам возможность оценить, какие значения достигаются функцией. Или, другими словами, позволяет найти набор всех изображений с помощью функции
Задача поиска точек, которые могут быть достигнуты функцией, очень полезна. Например, у вас может быть производственная функция \(q(x)\), которая дает вам объем вывода, полученный для \(x\) единиц ввода.
Мы хотели бы знать, сколько единиц ввода необходимо для производства \(b\) единиц вывода. Другими словами, нам нужно найти \(x\), чтобы \(q(x) = b\), что является еще одним способом узнать, находится ли \(b\) в диапазоне функции \(q(x)\).
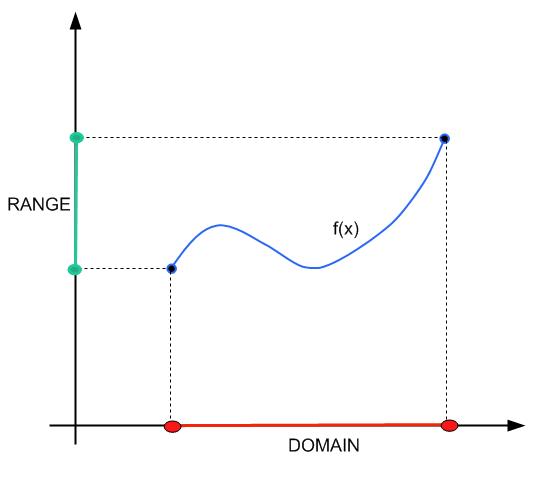
В этом уроке мы больше сконцентрируемся на механике нахождения диапазона. Для более концептуального подхода к домену и диапазону вы можете проверьте этот учебник .
Алгебраический способ определения диапазона функции
Так же, как когда мы узнали, как вычислить домен, не существует единого рецепта для нахождения диапазона, это действительно зависит от структуры функции \(f(x)\).
Тем не менее, всегда будет использоваться один алгебраический прием. ТАКИМ способом вы найдете диапазон. Обращать внимание:
Скажем, нам нужно получить диапазон заданной функции \(f(x)\). Затем мы рассмотрим типичное действительное число \(y\) и попытаемся решить для \(x\) следующее уравнение:
\[f(x) = y\]Нам нужно определить, для каких значений \(y\) приведенное выше уравнение может быть решено для \(x\). Вот и все. Конечно, это может быть сложно сделать, в зависимости от структуры функции \(f(x)\), но это то, что вам нужно сделать.
Итак, это алгебраический способ, способ найти диапазон функции без построения графиков.
ПРИМЕР 1
Найдите диапазон функции \(\displaystyle f(x) = \frac{x+1}{x-3}\):
ОТВЕЧАТЬ:
Мы продолжаем использовать алгебраический способ: пусть \(y\) будет числом, и мы решим для \(x\) в следующем уравнении: \(f(x) = y\). Значение \(y\) находится в диапазоне, если \(f(x) = y\) может быть решено для \(x\).
В этом случае мы имеем:
\[\large f(x) = y \Leftrightarrow \frac{x+1}{x-3} = y\] \[\Rightarrow \,\,\,x+1 = y\left( x-3 \right)\] \[\Rightarrow \,\,\,x+1 = yx-3y\] \[\Rightarrow \,\,\,x-yx=-1-3y\] \[\Rightarrow \,\,\,x\left( 1-y \right)=-1-3y\] \[\Rightarrow \,\,\,x=\frac{3y+1}{y-1}\]Следовательно, когда будет четко определено \(x\)? Почти для всех \(y\), кроме случая \(y = 1\), потому что в этом случае у нас есть деление на \(0\). Следовательно, диапазон \(f\) в этом случае - это вся вещественная линия, кроме 1.
Если мы используем обозначение интервалов, мы можем написать \(Range(f) = (-\infty, 1) \cup (1, +\infty)\).
ПРИМЕР 2
Найдите диапазон функции \(f(x) = x^2 - 4x + 3\):
ОТВЕЧАТЬ:
Опять же, мы продолжаем использовать алгебраический способ, поэтому вы знаете, что упражнение: Пусть \(y\) будет числом, и мы решим для \(x\) в следующем уравнении: \(f(x) = y\). Значение \(y\) находится в диапазоне, если \(f(x) = y\) может быть решено для \(x\).
В этом случае мы имеем:
\[\large f(x) = y \Leftrightarrow x^2 - 4x + 3 = y\] \[\Rightarrow \,\,\, x^2 - 4x + 3 - y = 0 \text{ (This is a quadratic equation in x)}\] \[\Rightarrow \displaystyle \,\,\, x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\] \[\Rightarrow \displaystyle \,\,\, x = \frac{-(-4) \pm \sqrt{(-4)^2 - 4(1)(3-y)}}{2(1)}\] \[\Rightarrow \displaystyle \,\,\, x = \frac{4 \pm \sqrt{16 - 4(3-y)}}{2}\] \[\Rightarrow \displaystyle \,\,\, x = \frac{4 \pm \sqrt{16 - 12 + 4y}}{2}\] \[\Rightarrow \displaystyle \,\,\, x = \frac{4 \pm \sqrt{4 + 4y}}{2}\] \[\Rightarrow \displaystyle \,\,\, x = 2 \pm \sqrt{1+y}\]Теперь, видя это последнее выражение, когда будет хорошо определено \(x\)? Нам нужно, чтобы аргумент квадратного корня был неотрицательным, поэтому нам нужно:
\[1+y \ge 0\]что означает, что \(y \ge -1\). Если мы используем обозначение интервалов, мы можем написать \(Range(f) = [-1, +\infty)\).
В этом примере мы могли бы решить эту проблему, используя тот факт, что \(f(x) = x^2 - 4x + 3\) является квадратичной функцией, а ее график представляет собой параболу, которая открывается вверх.
Точка минимума этой параболы достигается в вершине. Координата x вершины:
\[\displaystyle x_V = \frac{-b}{2a} =\frac{-(-4)}{2(1)} =\frac{4}{2} = 2\]Теперь координата y вершины просто определяется путем вставки значения \(x_V = 2\) в квадратичную функцию:
\[y_V = f(x_V) = 2^2 - 4(2) + 3 = -1\]Поскольку минимальное значение, достигаемое параболой, равно \(-1\), мы заключаем, что диапазон равен \([-1, +\infty)\), что является тем же выводом, что и найденный алгебраически.
График функции \(f(x) = x^2 - 4x + 3\) делает это еще более понятным:
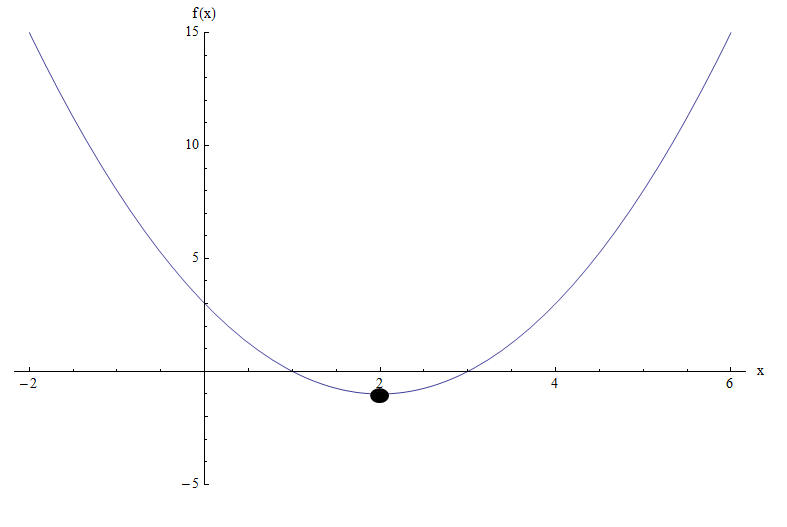
Мы можем видеть, что на основе графика минимум достигается в \(x = 2\), что в точности соответствует координате x вершины.
Риск использования графика для определения диапазона заключается в том, что вы потенциально можете неправильно прочитать критические точки на графике и дать неточную оценку того, где функция достигает своего максимума или минимума.
Другие стратегии поиска диапазона функции
Как мы видели в предыдущем примере, иногда мы можем найти диапазон функции, просто взглянув на ее график.
Например, вы хотите найти диапазон функции \(f(x) = x + 3\). График показан ниже:
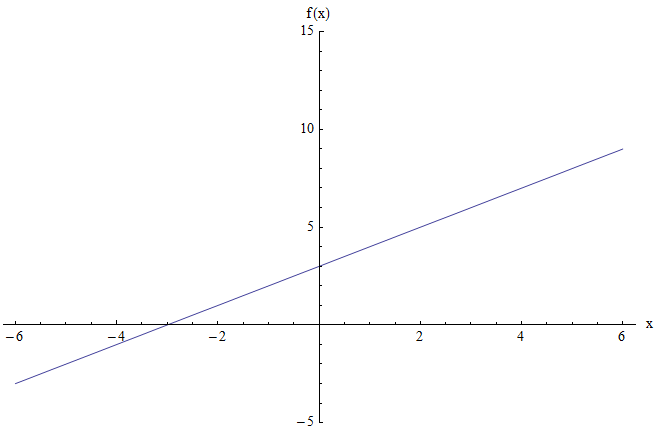
На графике выше не показаны минимальные или максимальные точки. Более того, когда \(x\) большое и положительное значение, значение функции также большое и положительное. И аналогично, когда \(x\) очень отрицательно, значение функции также очень отрицательное.
Интуиция подсказывает, что функция может принимать любые отрицательные и положительные значения, выбирая достаточно большие (положительные или отрицательные) значения \(x\). И тогда можно сделать вывод, что диапазон - это вся реальная линия, которая равна \((-\infty, +\infty)\) с использованием обозначения интервала.
Такой анализ верен с точки зрения результата, но ненадежен с точки зрения аргументации. У "графического метода" поиска диапазона есть та же проблема: он привлекателен с интуитивной точки зрения, но довольно скуден с точки зрения содержания.
Обычно, если возможно, мы должны предпочесть аналитический / алгебраический путь. В этом примере нам нужно найти \(x\):
\[x + 3 = y\] \[\Rightarrow \,\, x = y - 3\]Итак, есть ли какие-либо ограничения на \(y\) для правильного определения \(x\)? Вовсе нет, поэтому нет никаких ограничений на \(y\), и можно сделать вывод, что диапазон - это вся реальная линия.
Вы можете проверить эту статью, если хотите знать, как найти домен функции вместо.
Есть много веских алгебраических причин для нахождения диапазона, одна из них состоит в том, что он является частью процессов для найти обратную функцию .
