Алгебра Учебники

Горизонтальные асимптоты

В этом уроке мы рассмотрим концепцию горизонтальная асимптота и его наиболее важные приложения. Мы постараемся избежать каких-либо чрезмерно технических объяснений, но будем использовать некоторые элементы исчисления.

В основном, важная часть этого урока — это хорошее геометрическое представление о горизонтальных асимптотах. Давай начнем!

Что такое горизонтальная асимптота

Горизонтальная асимптота — это верхняя граница, которую можно представить в виде горизонтальной линии, задающей предел поведения графика заданной функции.

Это означает, что график функции \(f(x)\) как бы приближается к этой горизонтальной линии по мере увеличения значения \(x\).

Как найти горизонтальную асимптоту?

Понимание этого предельного горизонтального поведения функций, демонстрирующих эту характеристику, может оказаться очень полезным для поиска горизонтальных асимптот.

Действительно, при определенных обстоятельствах это ограничивающее поведение выглядит как горизонтальная линия для больших значений \(x\). См., например, функцию ниже.

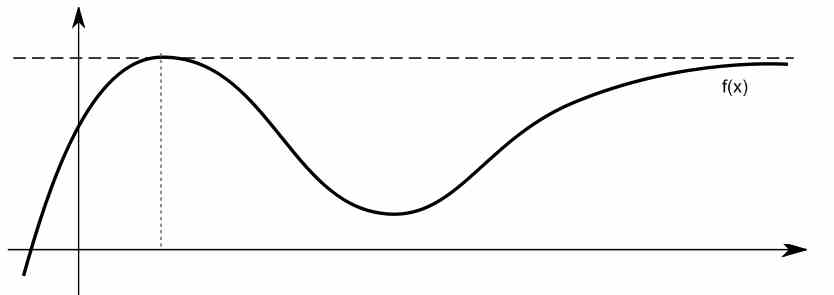
Как найти горизонтальную асимптоту функции, используя пределы?

Чтобы внести ясность в определение, горизонтальная линия \(y = h\) является горизонтальной асимптотой функции \(f(x)\), если

\[\large \lim_{x\to\infty} f(x) = h\]

если указанный выше предел существует и конечен. Для тех, кто еще не прошел курс математического анализа, горизонтальная линия \(y = h\) — это горизонтальная асимптота функции \(f(x)\), когда \(h\) — это предел \(f(x)\), когда \(x\) приближается к бесконечности. Что значит быть "пределом"? Это означает, что для достаточно больших значений \(x\) значение \(f(x)\) будет настолько близко к \(h\), насколько мы заранее определили. Фантазийно, правда?

Какова формула горизонтальной асимптоты?

Чтобы найти формулу горизонтальной асимптоты, нам сначала нужно найти соответствующий предел. Предположим, что у вас есть

\[\large \lim_{x\to\infty} f(x) = h\]

В этом случае мы скажем, что горизонтальная асимптота — это \(h\), а формула горизонтальной асимптоты — \(y = h\). Другими словами, горизонтальная асимптота проста – это горизонтальная линия, это линия с нулевым наклоном.

Это придает смысл тому, что означает горизонтальная асимптота с точки зрения пределов: найденный предел соответствует определению горизонтальной линии, которая называется горизонтальной асимптотой.

Пример 1

Найдите горизонтальную асимптоту функции

\[ \large f(x) = \frac{x^2}{x^2+1} \]

Отвечать:

Чтобы найти горизонтальную асимптоту, нам нужно найти предел функции \(f(x)\) при стремлении \(x\) к бесконечности. Если вы не знакомы с исчислением, сначала попробуйте вычислить функцию с очень большим значением \(x\).

Например, скажем, что \(x = 1,000,000\). Подставим это число в функцию:

\[ \large f(1,000,000) = \frac{1,000,000^2}{1,000,000^2+1} = \frac{1,000,000,000,000}{1,000,000,000,000+1}\] \[ = \frac{1,000,000,000,000}{1,000,000,000,001} = 0.999999999999 \]

что чертовски близко к 1. Тогда следует подозревать, что предел равен 1. На самом деле оказывается, что, когда \(x\) велико, значение \(x^2\) настолько велико по отношению к 1, что \(x^2\) очень похож на \(x^2 + 1\), по крайней мере, в относительном выражении. Итак, разделив числитель и знаменатель на \(x^2\):

\[ \large f(x) = \frac{x^2}{x^2+1} = \frac{1}{1+\frac{1}{x^2}} \rightarrow \frac{1}{1+0} = 1 \]

потому что \(\frac{1}{x^2}\) приближается к 0, а \(x\) приближается к бесконечности. Поэтому нетрудно доказать или убедиться в том, что

\[\large \lim_{x\to\infty} f(x) =\large \lim_{x\to\infty} \frac{x^2}{x^2+1} = 1\]

что означает, что горизонтальная асимптота равна \(y = 1\). Теперь будьте осторожны с ответом, если вы отвечаете на тест или домашнее задание. Некоторые люди скажут: "Горизонтальная асимптота равна 1", что неверно.

Технически горизонтальная асимптота — это функция \(y = 1\), а НЕ число 1. Горизонтальная асимптота — это постоянная функция, которая не совпадает с числом. Просто говорю, потому что есть некоторые привередливые оценщики.

Пример 2

Найдите горизонтальную асимптоту, если она существует для функции

\[ \large f(x) = \frac{x^3}{x^2+1} \]

Отвечать:

Разделив числитель и знаменатель на \(x^2\):

\[ \large f(x) = \frac{x}{1+\frac{1}{x^2}} \]

Но ждать! Здесь трюк не сработал? Да, это так. Обратите внимание, что знаменатель станет очень близким к 1, поскольку \(x\) станет очень большим, а числитель станет очень большим.

Нетрудно поверить, что \(f(x)\) сходится к бесконечности, так что горизонтальной асимптоты не существует. Каждый раз, когда мы видим неограниченную функцию, как в случае \(f(x)\) в этом примере, у нас не будет горизонтальной асимптоты.

Горизонтальная асимптота или горизонтальные асимптоты?

Технически может быть две горизонтальные асимптоты: одна слева и одна справа. Левая горизонтальная асимптота равна \(y = h_L\), если

\[\large \lim_{x \to -\infty} f(x) = h_L\]

Аналогично, правая горизонтальная асимптота равна \(y = h_R\), если

\[\large \lim_{x \to +\infty} f(x) = h_R\]

в случае, если любой из вышеуказанных пределов существует и конечен. Может случиться так, что функция имеет две горизонтальные асимптоты, имеет только одну горизонтальную асимптоту или не имеет ни одной.

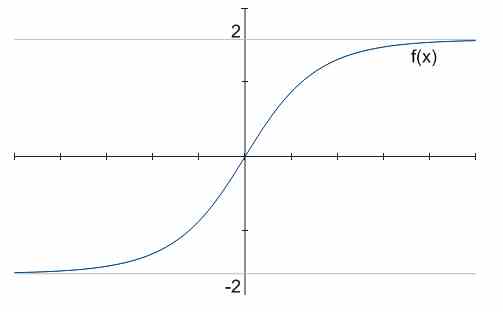
Например, на графике выше есть две горизонтальные асимптоты: \(y = -2\) и \(y = 2\).

По какому правилу находят горизонтальную асимптоту?

Не существует общих правил, подходящих для всех случаев. В общем случае нам нужно вычислить предел при приближении \(x\) к \(-\infty\) и предел при приближении \(x\) к \(+\infty\).

Если какой-либо из этих пределов существует и конечен, мы будем иметь горизонтальные асимптоты.

Одно конкретное правило можно разработать для случая, когда данная функция \(f(x)\) является частным двух многочленов. Если это так, предположим, что \(m\) — это порядок многочлена в числителе, а \(n\) — это порядок многочлена в знаменателе. Тогда мы имеем следующие случаи:

Дело 1: Если \(m < n\), то горизонтальная асимптота равна \(y = 0\).

Случай 2: Если \(m = n\) и \(a\) — старший коэффициент многочлена в числителе, а \(b\) — старший коэффициент многочлена в знаменателе, то горизонтальная асимптота равна \(\displaystyle y = \frac{a}{b}\).

Случай 3: Если \(m > n\), то горизонтальной асимптоты нет.

Пример 2

Найдите, если существует, горизонтальную асимптоту функции

\[\large f(x) = \frac{3x^2+2x-1}{2x^2 -x+2}\]

Отвечать:

Функция состоит из частного двух многочленов. Полином в числителе — это \(3x^2+2x-1\), который является многочленом порядка 2, поэтому \(m = 2\) и старшие коэффициенты 3.

Полином в знаменателе — это \(2x^2 -x+2\), который является многочленом порядка 2, поэтому \(n = 2\) и ведущей константой 2. Вы можете использовать нашу Калькулятор полиномов провести это разделение с указанием всех шагов.

Следовательно, поскольку в этом случае \(m = n\) существует горизонтальная асимптота, и она представляет собой частное старших коэффициентов, то в этом случае горизонтальная асимптота равна

\[\large y = \frac{3}{2}\]

Подробнее о горизонтальных асимптотах

Итак, ваш вопрос в том, как найти асимптоты уравнения, верно? Прежде всего, вы найдете асимптоты функция , а не уравнения. Затем вам нужно начать с общего определения, используя пределы.

Если вы не знаете математического анализа и не знаете, как вычислять пределы, то вам следует хотя бы попытаться подставить в функцию очень большие значения \(x\), а также очень отрицательные значения \(x\) и посмотреть, как функция ведет себя.

Даже построение графика функции с помощью какого-либо программного обеспечения может дать вам четкое представление о наличии горизонтальных асимптот.

В конечном счете, в очень ограниченном случае, когда функция является частное многочленов , то вы можете применить правило на основе ордеров \(m\) и \(n\).