Иногда простой вопрос, такой как квадратный корень из 64, имеет ответ, который может запутать несколько.В этом случае мы рассеиваем пару мифов.

Основная цель в этом уроке состоит в том, чтобы узнать несколько вещей о квадратных корнях и радикалах, чтобы вы могли отвечать на вопросы об этом без колебаний.

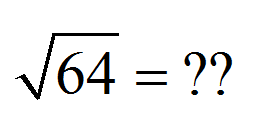
Первое, во-первых.Давайте изложим определение квадратного корня:

Квадратный корень данного номера положительный номер (или ноль) так что при квадратах приводит к тому данному количеству Отказ

Вот и все.Итак, учитывая номер __xxyz_a__, его квадратный корень - это номер \(b\), так что \(b \ge 0\) и

Посмотрев на вышеуказанное выражение, мы видим, что если \(b\) будет квадратный корень \(x\), то \(x = b^2\), и поскольку квадратный номер не может быть отрицательным, \(x\) может быть неотрицательным (если мы хотим иметь возможностьНайдите его квадратный корню).

Заключение : Мы можем только вычислить квадратные корни неотрицательных значений \(x\).Или сказал по-другому, Домен функции \(\sqrt x\) - \([0,+\infty)\).

Итак, отвечая на наш начальный вопрос: Что такое квадратный корень из 64?

На основании того, что мы определили, нам нужно найти неотрицательное значение \(b\), так что \(b^2 = 64\).Любое число встречи с этими свойствами приходят на ум?

Ну да, что если мы попробовали с \(b = 8\)?Хорошо, так \(b = 8\) неотрицательно, а \(b^2 = 8^2 = 64\).

Итак, мы нашли квадратный корень из 64, что составляет 8, потому что 8 не отрицательный, а \(8^2 = 64\).Мы пишем это как:

Миф о квадратной корневой функции

Теперь мы идем к теме, которая мотивировала этот учебник ... Вышеуказанное определение, приведенное к квадратному корню, позволяет отменить общее утверждение, что "квадратный корень из 64 плюс или минус 8", что не так.Действительно

Теперь мы можем понять, почему такой миф несет.Действительно, оба 8 и -8 имеют свойство, которое \(8^2 = 64\) и \((-8)^2 = 64\).Итак, почему -8 не квадратный корень из 64?

Потому что по определению мы сказали, что квадратный корню должен быть таким неотрицательным номером, который имеет свойство, которое при квадрате они равны данному числу.И -8 не удается, состояние неотрицательного.

График функции квадратной корневой

Посмотрите на график функции квадратного корня ниже:

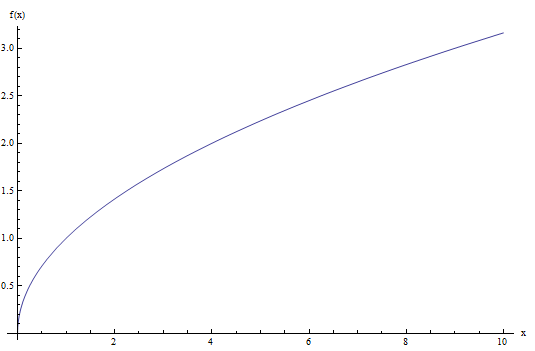
Как видите, эта функция принимает только не отрицательные значения, и она фактически проходит тест вертикальной линии, поэтому это функция.

Таким образом, в конце концов, определение квадратного корня в виде неотрицательного \(b\), так что \(b^2 = x\) делает квадратный корневой функцию.

Если на самом деле у нас было то, что \(\sqrt{64} = \pm 8\), то \(\sqrt x\) не будет функцией, вместо этого будет отношение, потому что вертикальная линия в \(x = 64\) будет пересекать график дважды (в 8 и -8).

Как насчет других радикальных функций?

Есть и другие типы радикальных функций.Например, кубический корня \(\sqrt[3] x\).В этом случае нет необходимости делать правило для того, что радикально выбрать, потому что кубический корень данного числа \(x\) - это число \(b\), так что \(b^3 = x\).

Кубический корень

Для кубического корня нет необходимости делать различия, потому что для данного \(x\) будет всего один номер \(b\) такой, что \(b^3 = x\).

Например

Просто потому, что \(4^3 = 64\).Или

Просто потому, что \((-4)^3 = -64\).Это, нет неоднозначности, как в случае квадратного корня.

Кварцевый корень

Для корня кварцевого корня он похож на квадратный корень.У нас будет это \(\sqrt[4] x = b\), если \(b \ge 0\) и \(b^4 = x\).

Например

Потому что \(2^4 = 16\) и \(2 \ge 0\).Но

Потому что хотя \((-2)^4 = -16\), у нас есть что \(-2 < 0\), так что то, что нетриское состояние не выполнено.

Как насчет N-го корня \(\sqrt[n] x\) в целом ???.

Я уверен, что вы угадали это.

Для \(n\) даже ситуация похожа на квадратный корню: \(\sqrt[n] x = b\), если \(b \ge 0\) и \(b^n = x\).

Для \(n\) странно, ситуация похожа на квадратный корню: \(\sqrt[n] x = b\), если \(b^n = x\).