Residual Sum of Squares Calculator
Instructions: Use this residual sum of squares to compute \(SS_E\), the sum of squared deviations of predicted values from the actual observed value. You need type in the data for the independent variable \((X)\) and the dependent variable (\(Y\)), in the form below:
What is the Residual Sum of Squares?
Mathematically speaking, a sum of squares corresponds to the sum of squared deviation of a certain sample data with respect to its sample mean. For a simple sample of data \(X_1, X_2, ..., X_n\), the sum of squares (\(SS\)) is defined as:
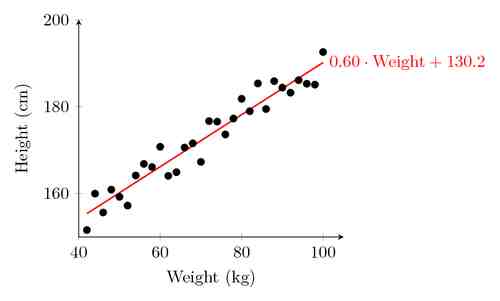
\[ SS = \displaystyle \sum_{i=1}^n (X_i - \bar X)^2 \]Now, when we are dealing with linear regression, what do we mean by Residual Sum of Squares? In this case we have paired sample data \( (X_i , Y_i) \), where X corresponds to the independent variable and Y corresponds to the dependent variable. The residual sum of squares \(SS_E\) is computed as the sum of squared deviation of predicted values \(\hat Y_i\) with respect to the observed values \(Y_i\). Mathematically:
\[ SS_E = \displaystyle \sum_{i=1}^n (\hat Y_i - Y_i)^2 \]A simpler way of computing \(SS_E\), which leads to the same value, is
\[ SS_E = SS_T - SS_E = SS_T - \hat \beta_1 \times SS_{XY} \]Other calculated Sums of Squares
There are other types of sum of squares. For example, if instead you are interested in the squared deviations of predicted values with respect to the average, then you should use this regression sum of squares calculator . There is also the cross product sum of squares, \(SS_{XX}\), \(SS_{XY}\) and \(SS_{YY}\).
What else can you do with pair data like these?
There are other things you could do with paired data like (\(X_i, Y_i\), such as computing the associated correlation coefficient , or also you may be interested in computing the linear regression equation with all the steps .