हाइपरबोला
एक हाइपरबोला समन्वय अक्षों में बिंदुओं का ज्यामितीय स्थान है जिसमें संपत्ति है कि दो निश्चित बिंदुओं (foci) तक दूरी के बीच का अंतर एक स्थिर के बराबर है, जिसे हम \(2a\) को कम करते हैं।
स्वाभाविक रूप से, यह थोड़ा सा भयभीत और बहुत तकनीकी लगता है, लेकिन वास्तव में एक हाइपरबोला परिभाषित किया गया है।
शायद, अगर मैं आपको हाइपरबोला का समीकरण देता हूं, तो आप इसे "पहचान" लेंगे।
आइए कोशिश करें: यह एक बहुत ही सामान्य हाइपरबोला का समीकरण है:
क्या आप यह समझ सकते हैं कि यह सिर्फ इसके समीकरण की जांच करके कैसा दिखता है?शायद नहीं।तो मैं आपके लिए ग्राफिक रूप से हाइपरबोला पेश करता हूं:
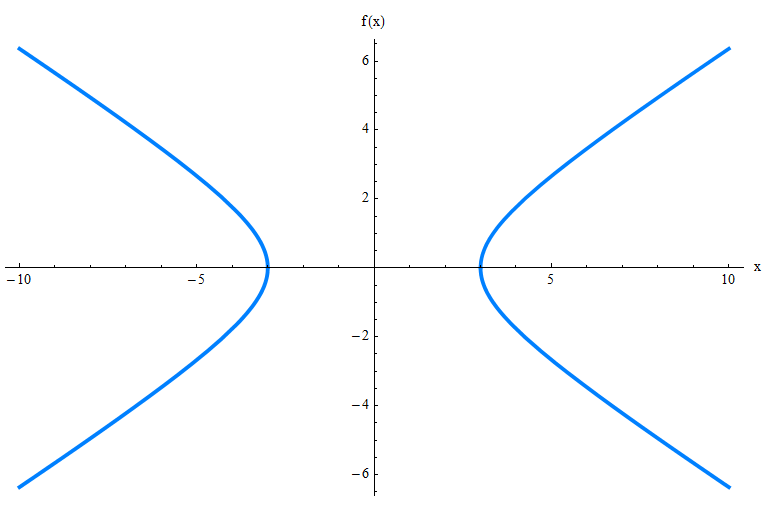
उपर्युक्त ग्राफ आपको केवल हाइपरबोला का ग्राफ दिखाता है, लेकिन कई अन्य तत्व हैं जिन्हें आपको अवगत होने की आवश्यकता है, जैसे कि पतला asymptotes, costices और foci।नीचे दिए गए ग्राफ की जाँच करें।
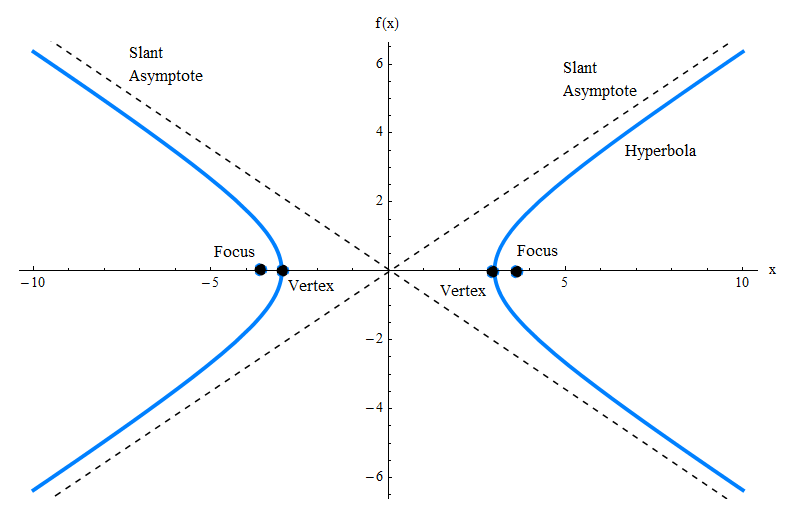
हाइपरबोला के सामान्य समीकरण
सैद्धांतिक चर्चा के बिना, हम बताएंगे कि एक्स-अक्ष पर फॉसी के साथ हाइपरबोला का सामान्य समीकरण है
\[\large \displaystyle \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 \]
उपरोक्त समीकरण द्वारा वर्णित हाइपरबोला के लिए, यह अंक \((-a, 0)\) और \((a, 0)\) पर शिखर है और इसमें अंक \((-c, 0)\) और \((c, 0)\) पर foci है, जहां \(c = \sqrt{a^2 + b^2}\)।
इस हाइपरबोला की एक दिलचस्प विशेषता यह है कि इसमें दो स्लंट एसिम्प्टोट्स हैं
Asymptote 1
: \(\displaystyle y = \frac{b}{a}x\)
Asymptote 2
: \(\displaystyle y = -\frac{b}{a}x\)
अब हाइपरबोला के समीकरण के साथ क्या होता है, यदि इसके बजाय किसी दिए गए बिंदु \((k,h)\) द्वारा शिखर का अनुवाद किया जाता है?
आपको बस उस मामले में करना है \(x\) \(x-k\) द्वारा प्रतिस्थापित किया गया है, और \(y\) को \(x-h\) द्वारा प्रतिस्थापित करें।
इसलिए, अनुवाद करके, हम प्राप्त करते हैं कि एक सामान्य हाइपरबोला का समीकरण है
\[\large \boxed{\displaystyle \frac{(x-k)^2}{a^2} - \frac{(y-h)^2}{b^2} = 1 }\]उपरोक्त हाइपरबोला में अंक \((k-a, h)\) और \((k+a, h)\) पर शिखर है और इसमें अंक \((k-c, h)\) और \((k+c, h)\) पर foci है, जहां \(c = \sqrt{a^2 + b^2}\)।
Slant asymptotes के समीकरण \(y = \frac{b}{a}(x-k) + h\) और \(y = -\frac{b}{a}(x-k) + h\) हैं।
वाई-अक्ष के साथ खुलने वाले हाइपरबोलास के साथ क्या होता है?
समरूपता द्वारा, हमें बस इतना करना है कि हम पहले से ही हाइपरबोला के सामान्य समीकरण में \(x\) और \(y\) की भूमिकाओं को प्रतिस्थापित करना है।व्यावहारिकता में, इसका मतलब यह है कि जहां भी \(x\) पराबोला के समीकरण में दिखाई देता है, हम इसे \(y\) बदलते हैं, और इसके विपरीत \(y\) के लिए।
तो फिर, एक हाइपरबोला के मामले में जो लंबे समय तक एक्स-अक्ष खोलता है, सामान्य समीकरण है
\[\large \boxed{\displaystyle \frac{(y-h)^2}{b^2} - \frac{(x-k)^2}{a^2} = 1 }\]उपरोक्त हाइपरबोला में अंक \((k, h - b)\) और \((k, h+b\) पर शिखर है और इसमें अंक \((k, h-c)\) और \((k, h+c)\) पर foci है, जहां \(c = \sqrt{a^2 + b^2}\)।
Slant asymptotes के समीकरण \(y = \frac{b}{a}(x-k) + h\) और \(y = -\frac{b}{a}(x-k) + h\) हैं।
उदाहरण 1
हाइपरबोला के foci, शिखर और slant asymptotes खोजें:
\[\large \displaystyle \frac{(y-2)^2}{9} - \frac{(x-4)^2}{16} = 1 \]उत्तर:
यह हाइपरबोला वाई-अक्ष के साथ खुलता है।इस मामले में, अनुवाद मान \(k = 4\) और \(h = 2\) हैं।इसके अलावा, हम उस \(a = \sqrt{16} = 4\) और \(b = \sqrt{9} = 3\) प्राप्त करते हैं।इसलिए, हम उस \(c = \sqrt{a^2+b^2} = \sqrt{4^2+3^2} = \sqrt{25} = 5\) को प्राप्त करते हैं।
इसलिए, foci \((k, h-c) = (4, 2 - 5) = (4, -3)\) और \((k, h+c) = (4, 2 + 5) = (4, 7)\) हैं।
शिखर \((k, h-b) = (4, 2 - 3) = (4, -1)\) और \((k, h+b) = (4, 2 + 3) = (4, 5)\) हैं।
पतला asymptotes हैं
\[\displaystyle y = \frac{b}{a}(x-k) + h = \frac{3}{4}(x-4) + 2\] \[\displaystyle y = -\frac{b}{a}(x-k) + h = \frac{3}{4}(x-4) + 2\]ग्राफिक रूप से:
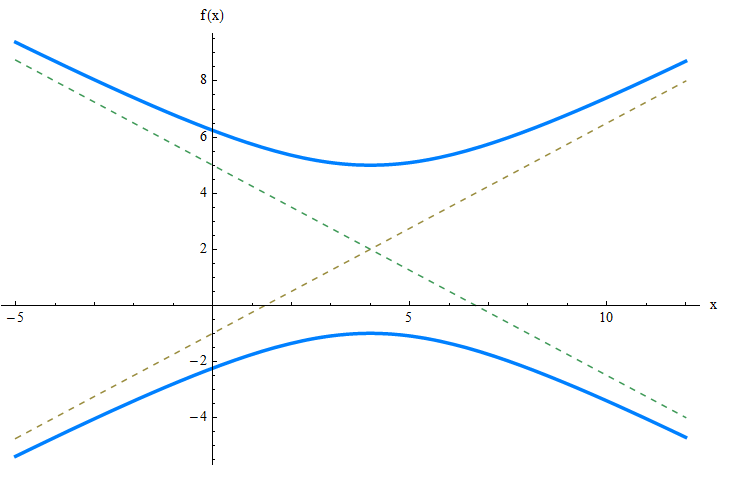
उदाहरण 2
\((-4, 0)\) और \((4, 0)\) Vertex पर foci के साथ हाइपरबोला के समीकरण को खोजें, \((6, 0\) पर ध्यान केंद्रित करें।
उत्तर:
ध्यान दें कि एफओसीआई और शिखर एक्स-अक्ष पर हैं, इसलिए हाइपरबोला एक्स-अक्ष के साथ खुलता है।इसके अलावा, चूंकि फॉसी मूल के संबंध में सममित हैं, और एक वर्टेक्स \((4, 0)\) है, हमें वह \(a = 4\) मिलता है।और चूंकि एक फोकस \((6, 0)\) पर है, इसलिए हमें वह \(b = \sqrt{6^2 - 4^2} = \sqrt{20} = 2\sqrt 5\) मिलता है।
इसलिए, हाइपरबोला का समीकरण है:
\[\large \displaystyle \frac{(y-h)^2}{b^2} - \frac{(x-k)^2}{a^2} = 1 \] \[\large \displaystyle \Rightarrow \frac{x^2}{16} - \frac{y^2}{20} = 1 \]हाइपरबोला और सामान्य शंकु वर्ग
पैराबोला के मामले के साथ ही, हाइपरबोला शंकु से कसकर संबंधित है।दरअसल अपोलोनियस नामक एक यूनानी गणितज्ञ एक व्यक्ति है जिसने शंकु वर्गों की अवधारणा को समझकर इस कनेक्शन की खोज की।
एक शंकु खंड तब होता है जब आप एक विमान के साथ शंकु का कटौती करते हैं, और शंकु के सापेक्ष कोण और कट के बिंदु पर विमान के आधार पर, शंकु एक ऐसे तरीके से कट जाता है जिसमें क्रॉस सेक्शन में एक विशिष्ट आकार होता है।
इसलिए, कट के सापेक्ष कोण के आधार पर हमारे पास अनुभाग के विभिन्न आकार हैं, और ये पैराबोला, सर्कल, अंडाकार, और हाइपरबोला हैं।नीचे दिए गए ग्राफ को देखें:
हाइपरबोला के बारे में अधिक
उत्पत्ति पर वर्टेक्स के साथ एक हाइपरबोला, जो एक्स-अक्ष के साथ खुलता है, समीकरण \(\displaystyle \frac{x^2}{a^2} - \frac{y^2}{a^2} = 1 \) है, जबकि एक हाइपरबोला, जो वाई-अक्ष के साथ खुलता है, समीकरण \(\displaystyle \frac{y^2}{a^2} - \frac{x^2}{a^2} = 1 \) है।
फिर, किसी दिए गए बिंदु \((k, h)\) में अनुवाद लागू करके एक सामान्य वर्टेक्स प्राप्त किया जा सकता है।
अनुप्रयोग
हाइपरबोला में व्यावहारिक दुनिया, साथ ही खगोल विज्ञान में कई अनुप्रयोग हैं।PARABOLA के साथ एक अंतर यह है कि हाइपरबोला में slant asymptotes है, जो PARABOLA के पास नहीं है।
बीजगणितीय रूप से बोलते हुए, एक हाइपरबोला एक अंडाकार जैसा होता है जो एक पैराबोला करता है, हालांकि एलिप्स के साथ साइन इन अंतर इसके आकार और गुणों में अंतर की दुनिया बनाता है।
एक और महत्वपूर्ण प्रकार का शंकु अनुभाग पैराबोला है, जिसमें से आप इसमें सीख सकते हैं ट्यूटोरियल ।इसके अलावा, आप भी सब कुछ सीख सकते हैं सर्कल के बाद में जानें तथा दीधवोधत ।