दीर्घवृत्त
एक दीर्घवृत्त समन्वय अक्षों में बिंदुओं का ज्यामितीय स्थान है जिसमें संपत्ति है कि अंडाकार के किसी दिए गए बिंदु की दूरी की संख्या दो निश्चित बिंदुओं (foci) को एक स्थिर के बराबर है, जिसे हम \(2a\) को संप्रदाय मानते हैं।
एक "ज्यामितीय स्थान" की अवधारणा एक वैचारिक दृष्टिकोण से बहुत आकर्षक है, लेकिन यह आपको उस बारे में स्पष्ट दृष्टिकोण नहीं दे सकती है जिसे आप चित्रित करने की कोशिश कर रहे हैं।
कोशिश करें और नीचे समीकरण समीकरण देखने का अभ्यास करें और देखें कि क्या आप यह समझ सकते हैं कि यह ग्राफिक रूप से क्या दिखता है;
क्या आप यह समझ सकते हैं कि उपरोक्त समीकरण को देखकर ग्राफ कैसे हो सकता है।मुझे ऐसा लगा।मुझे आपके लिए दीर्घवृत्त पेश करने दें:
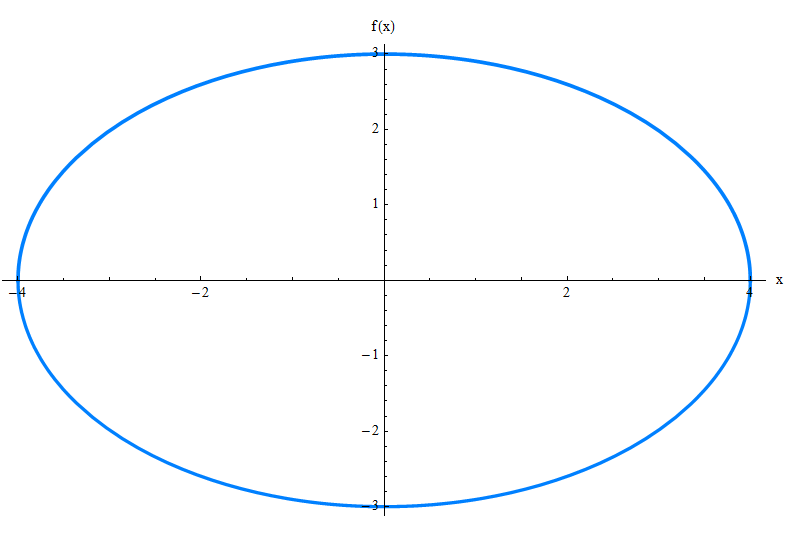
दीर्घवृत्त के सामान्य समीकरण
सैद्धांतिक चर्चा के बिना, हम बताएंगे कि मूल में केंद्र के साथ दीर्घवृत्त के सामान्य समीकरण, और एक्स-अक्ष पर foci के साथ, \(a \ge b\) के लिए है
\[\large \displaystyle \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \]
ऊपर वर्णित एलिप्स के लिए, इसमें अंक \((-c, 0)\) और \((c, 0)\) पर foci है, जहां \(c = \sqrt{a^2 - b^2}\)।
अब \(b > a\) जब उपरोक्त हाइपरबोला के समीकरण के साथ क्या होता है?
उस स्थान में, एफओसी वाई-अकष पर हैं, और वे \((0, -c)\) और \((0, c)\) हैं, जो \(c = \sqrt{b^2 - a^2}\)।
अब, अगर हुम केंद्र को एक बिन्दु \((k,h)\) पर विजापित करना चेके थे?
आपको बस उस में माले में करना है \(x\) \(x-k\) dva _ \(x-k\) dva वर __
इलिए, अनुवाद कर्क, कुछ मिलता है
\[\large \boxed{\displaystyle \frac{(x-k)^2}{a^2} + \frac{(y-h)^2}{b^2} = 1 }\]उपरोक्त एलिप्स में\((k,h)\)पर एक केंद्र है और इसमें\((k-c, h)\)और\((k+c, h)\)परफोकीहै जहां\(a \ge b\)के लिए\(a \ge b\),और\((k, h-c)\)और\((k, h+c)\)जहां\(c = \sqrt{b^2 - a^2}\)\(b>a\)के लिए।
उदाहरण 1
Ellipse के foci खोजाग:
\[\large \displaystyle \frac{x^2}{9} + \frac{y^2}{16} = 1 \]उत्तर:
सबसे पहले,ऊपर समीकरण की संरचना के आधार पर,एलिप्स मूल\((0, 0)\)पर केंद्रित है.ध्यान दें कि प्रमुख अर्ध अक्ष4है,जो\(9y\)से जुड़ा हुआ है,इसलिएफोकीवाई-अक्ष पर है।
समीकरण से हम \(a^2 = 9\) और \(b^2 = 16\) prapt ciya.hm पाटे हैं \(c = \sqrt{b^2 - a^2} = \sqrt{16 - 9} = \sqrt 7\)। Ilii, foci \((0, -\sqrt{7})\) और \((0, \sqrt{7})\) पर है।
उदाहरण 2
\((0, 2)\) पर केंद्रित एलिप्स के समीरन को \((6, 2)\) पर एक फोकस के साथ और 3 के लिए के लिए एक अर्ध-ममूली अक्ष के साथ।
उत्तर:
प्रडान की गड़ी जानकारी के आधार पर, \(c = 6 - 0 = 6\)। चक्की फोकि एक तर्धन से एक्स-अक्श के सिस्टम है, इसलिल हदह \(b = 3\) और फिर \(a = \sqrt{6^2 - 3^2} = \sqrt{27}\) मिलता है
इलिए, दीर्ज़वोधत का समीरन है:
\[\large \displaystyle \frac{x^2}{27} + \frac{(y-2)^2}{9} = 1 \]दीरहवतेत और सामन्य शंकु कुरग
पैराबोला,हाइपरबोला और सर्कल के मामले के समान,दीर्घवृत्त शंकु से संबंधित है.एपोलोनियस नामक प्राचीन यूनानी गणितज्ञ ने इस संबंध की खोज की,जिसे कहा जाता है शंकु अनुभूति ।
एक शंकु अनुभाग उन आकारों से मेल खाता है जब आप एक विमान के साथ एक शंकु के माध्यम से कटौती करते हैं,और शंकु और विमान के सापेक्ष कोण के आधार पर,क्रॉस सेक्शन के आकार में परिवर्तन करते हैं।
दरअसल,कोण और विमान कोण के आधार पर एक दूसरे का सामना करना पड़ता है,क्रॉस सेक्शन का आकार एक पैराबोला,सर्कल,एलिप्स,या हाइपरबोला हो सकता है.यह नीचे दिए गए ग्राफ में चित्रित किया गया है:
दीरवोधत के बाद में अधिकृत
समीरन \(\displaystyle \frac{x^2}{a^2} + \frac{y^2}{a^2} = 1 \) के साथ एक दीधवती के लिए, \(a \ge b\) के साथ, \(a\) को अर्ध-उपधुख धूरी ने जाबा है, और \(b\) को अर्ट-ममूली धूरी ने जा सका।
अब, \(b > a\) के लिए, कि मूलवर्ग को उलट दया है, इस्लिए \(a\) को अर्ट-ममूली धूरी नेगा, और \(b\) को अर्ध-प्रमूक धूरी 'जागता है।
सनक
उद्ध्ण सूत्र का उपयोग करने के लिए एक दीर्दवतनत की विलक्ष्य की गणना की जानी है:
\[\displaystyle e = \sqrt{1 - \left( \frac{b}{a}\right)^2}\]यह सनकी पैरामीटर शोर इंगित करता है कि एलआईपीएस का एएआरएआरएक्सएआरए के एक सम्यित संस्करणों से कितना प्रोस्थान करता है (जो सर्कल है, जिसमेन सनकीपन \(e = 1\) है)।
अनुप्र्योग
एलिप्स में इतने सारे एप्लिकेशन हैं.विज्ञान में,यह बड़े पैमाने पर खगोल विज्ञान में उपयोग किया जाता है.दरअसल,ग्रह सूर्य के चारों ओर अंडाकार कक्षाओं का वर्णन करते हैं।
बीजगण्यती रूप से एक दीर्दवोधित एक हाइपरोबोला के लिए बहुत सावधानी है, लेकिन बेईकी ग्यू म्यूल रूपर से अलग हैग।
आग पैराबोला के बाद में भी सेखने में रुची लेते हैं ट्यूटोरियल .आप हमरे पहाड़ी भी देखने के लिए हैं हिपरबोला ट्यूटोरियल नगर सर्कल के बाद में जानें ।