रेंज कैसे खोजें
बीजगणित और कैलकुलस में किसी फ़ंक्शन की सीमा को खोजने का तरीका सीखना बहुत महत्वपूर्ण साबित हो सकता है, क्योंकि यह आपको यह आकलन करने की क्षमता देता है कि किसी फ़ंक्शन द्वारा कौन से मान प्राप्त किए जाते हैं। या दूसरे शब्दों में, यह आपको फ़ंक्शन के माध्यम से सभी छवियों के सेट को खोजने की अनुमति देता है
किसी फ़ंक्शन द्वारा किन बिंदुओं तक पहुंचा जा सकता है, यह पता लगाने का कार्य बहुत उपयोगी है। उदाहरण के लिए, आपके पास एक उत्पादन फलन \(q(x)\) हो सकता है, जो आपको \(x\) इनपुट की इकाइयों के लिए प्राप्त आउटपुट की मात्रा देता है।
हम जानना चाहेंगे कि आउटपुट की \(b\) इकाइयों का उत्पादन करने के लिए कितनी इनपुट इकाइयों की आवश्यकता है। तो दूसरे शब्दों में, हमें \(x\) खोजने की आवश्यकता है ताकि \(q(x) = b\), जो यह पूछने का एक और तरीका है कि \(b\) फ़ंक्शन \(q(x)\) की सीमा में है या नहीं।
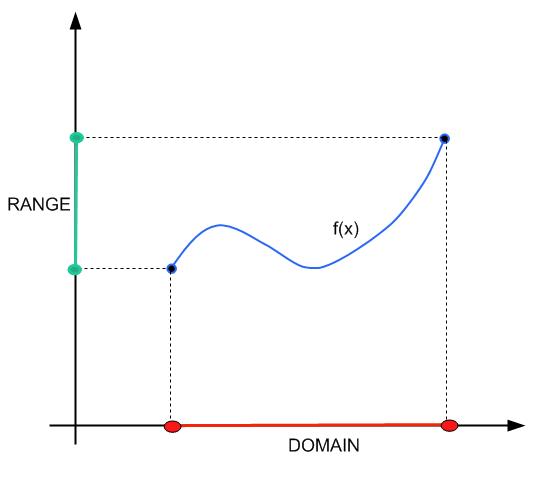
इस ट्यूटोरियल में हम परास खोजने के यांत्रिकी पर अधिक ध्यान देंगे। डोमेन और रेंज के लिए अधिक वैचारिक दृष्टिकोण के लिए, आप कर सकते हैं इस ट्यूटोरियल की जाँच करें .
किसी फलन का परिसर ज्ञात करने का बीजीय तरीका
उसी तरह जब हमने सीखा कि डोमेन की गणना कैसे की जाती है, तो रेंज खोजने के लिए एक नुस्खा नहीं है, यह वास्तव में \(f(x)\) फ़ंक्शन की संरचना पर निर्भर करता है।
फिर भी, एक बीजीय तकनीक है जिसका हमेशा उपयोग किया जाएगा। यह वह तरीका है जिससे आप सीमा का पता लगाते हैं। ध्यान दें:
मान लें कि हमें किसी दिए गए फ़ंक्शन \(f(x)\) की सीमा प्राप्त करने की आवश्यकता है। फिर, हम एक सामान्य वास्तविक संख्या \(y\) पर विचार करेंगे और हम \(x\) के लिए निम्नलिखित समीकरण को हल करने का प्रयास करेंगे:
\[f(x) = y\]हमें यह निर्धारित करने की आवश्यकता है कि \(y\) के किन मानों के लिए उपरोक्त समीकरण को \(x\) के लिए हल किया जा सकता है। यही वह है। बेशक, \(f(x)\) फ़ंक्शन की संरचना के आधार पर, ऐसा करना कठिन हो सकता है, लेकिन आपको यह करने की आवश्यकता है।
तो यह बीजीय तरीका है, बिना रेखांकन के किसी फ़ंक्शन की सीमा कैसे प्राप्त करें।
उदाहरण 1
फ़ंक्शन की सीमा ज्ञात करें \(\displaystyle f(x) = \frac{x+1}{x-3}\):
उत्तर:
हम बीजीय तरीके से आगे बढ़ते हैं: मान लीजिए \(y\) एक संख्या है और हम निम्नलिखित समीकरण में \(x\) के लिए हल करेंगे: \(f(x) = y\)। यदि \(f(x) = y\) को \(x\) के लिए हल किया जा सकता है, तो मान \(y\) सीमा में है।
इस मामले में हमारे पास है:
\[\large f(x) = y \Leftrightarrow \frac{x+1}{x-3} = y\] \[\Rightarrow \,\,\,x+1 = y\left( x-3 \right)\] \[\Rightarrow \,\,\,x+1 = yx-3y\] \[\Rightarrow \,\,\,x-yx=-1-3y\] \[\Rightarrow \,\,\,x\left( 1-y \right)=-1-3y\] \[\Rightarrow \,\,\,x=\frac{3y+1}{y-1}\]इसलिए, \(x\) को कब अच्छी तरह परिभाषित किया जाएगा? लगभग सभी \(y\) के लिए, जब \(y = 1\) को छोड़कर, क्योंकि उस स्थिति में हमारे पास \(0\) द्वारा एक विभाजन होता है। इसलिए, इस मामले में \(f\) का परिसर 1 को छोड़कर पूरी वास्तविक रेखा है।
यदि हम अंतराल संकेतन का उपयोग करते हैं, तो हम \(Range(f) = (-\infty, 1) \cup (1, +\infty)\) लिख सकते हैं।
उदाहरण 2
फ़ंक्शन की सीमा ज्ञात करें \(f(x) = x^2 - 4x + 3\):
उत्तर:
फिर से, हम बीजगणितीय तरीके से आगे बढ़ते हैं, ताकि आप ड्रिल को जान सकें: मान लें कि \(y\) एक संख्या है और हम निम्नलिखित समीकरण में \(x\) के लिए हल करेंगे: \(f(x) = y\)। यदि \(f(x) = y\) को \(x\) के लिए हल किया जा सकता है, तो मान \(y\) सीमा में है।
इस मामले में हमारे पास है:
\[\large f(x) = y \Leftrightarrow x^2 - 4x + 3 = y\] \[\Rightarrow \,\,\, x^2 - 4x + 3 - y = 0 \text{ (This is a quadratic equation in x)}\] \[\Rightarrow \displaystyle \,\,\, x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\] \[\Rightarrow \displaystyle \,\,\, x = \frac{-(-4) \pm \sqrt{(-4)^2 - 4(1)(3-y)}}{2(1)}\] \[\Rightarrow \displaystyle \,\,\, x = \frac{4 \pm \sqrt{16 - 4(3-y)}}{2}\] \[\Rightarrow \displaystyle \,\,\, x = \frac{4 \pm \sqrt{16 - 12 + 4y}}{2}\] \[\Rightarrow \displaystyle \,\,\, x = \frac{4 \pm \sqrt{4 + 4y}}{2}\] \[\Rightarrow \displaystyle \,\,\, x = 2 \pm \sqrt{1+y}\]अब, इस अंतिम अभिव्यक्ति को देखते हुए, \(x\) को कब अच्छी तरह परिभाषित किया जाएगा? हमें चाहिए कि वर्गमूल का तर्क गैर-ऋणात्मक होना चाहिए, इसलिए हमें चाहिए:
\[1+y \ge 0\]जिसका अर्थ है कि \(y \ge -1\)। यदि हम अंतराल संकेतन का उपयोग करते हैं, तो हम \(Range(f) = [-1, +\infty)\) लिख सकते हैं।
इस उदाहरण में, हम इस तथ्य का उपयोग करके इसे हल कर सकते थे कि \(f(x) = x^2 - 4x + 3\) एक द्विघात फलन है, और इसका ग्राफ एक परवलय है जो ऊपर की ओर खुलता है।
इस परवलय का न्यूनतम बिंदु शीर्ष पर पहुँच जाता है। शीर्ष का x-निर्देशांक है:
\[\displaystyle x_V = \frac{-b}{2a} =\frac{-(-4)}{2(1)} =\frac{4}{2} = 2\]अब, शीर्ष का y-निर्देशांक केवल द्विघात फलन में \(x_V = 2\) मान को प्लग करके पाया जाता है:
\[y_V = f(x_V) = 2^2 - 4(2) + 3 = -1\]चूँकि परवलय द्वारा पहुँचा गया न्यूनतम मान \(-1\) है, इसलिए हम यह निष्कर्ष निकालते हैं कि परास \([-1, +\infty)\) है, जो बीजगणितीय रूप से प्राप्त निष्कर्ष के समान ही है।
फंक्शन \(f(x) = x^2 - 4x + 3\) का ग्राफ इसे और भी स्पष्ट करता है:
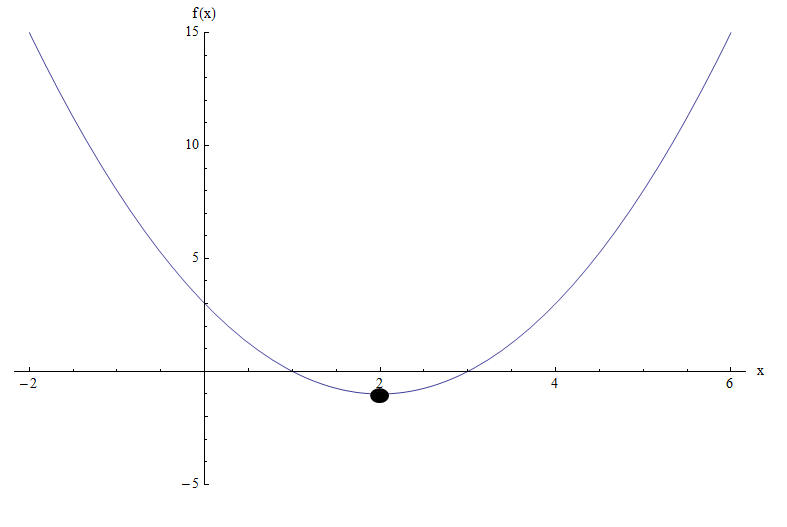
हम देख सकते हैं कि, ग्राफ के आधार पर, न्यूनतम \(x = 2\) पर पहुंच गया है, जो कि शीर्ष के x-निर्देशांक में ठीक वैसा ही पाया गया था।
श्रेणी को खोजने के लिए ग्राफ़ का उपयोग करने का जोखिम यह है कि आप संभावित रूप से ग्राफ़ में महत्वपूर्ण बिंदुओं को गलत तरीके से पढ़ सकते हैं और फ़ंक्शन के अधिकतम या न्यूनतम तक पहुंचने का गलत मूल्यांकन दे सकते हैं।
किसी फ़ंक्शन की रेंज ढूँढने के लिए अन्य रणनीतियाँ
जैसा कि हमने पिछले उदाहरण में देखा, कभी-कभी हम किसी फ़ंक्शन की सीमा केवल उसके ग्राफ़ को देखकर पा सकते हैं।
उदाहरण के लिए, मान लें कि आप \(f(x) = x + 3\) फ़ंक्शन की सीमा ज्ञात करना चाहते हैं। ग्राफ नीचे दिखाया गया है:
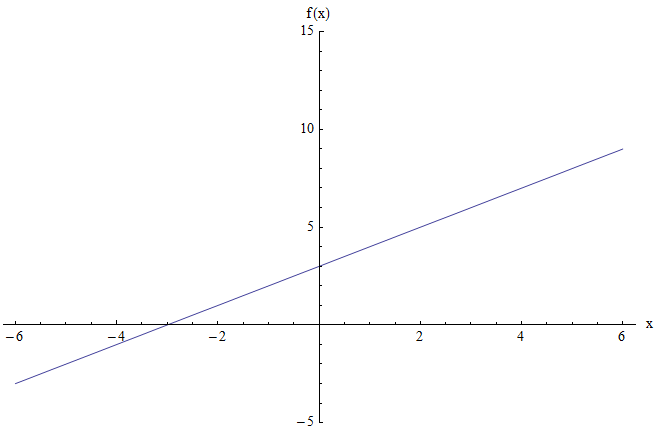
ऊपर दिया गया ग्राफ कोई न्यूनतम या अधिकतम अंक नहीं दिखाता है। इसके अलावा, जब \(x\) बड़ा और धनात्मक होता है, तो फलन का मान भी बड़ा और धनात्मक होता है। और इसी तरह, जब \(x\) बहुत ऋणात्मक होता है, तो फलन का मान भी बहुत ऋणात्मक होता है।
अंतर्ज्ञान यह है कि फ़ंक्शन बड़े पर्याप्त (सकारात्मक या नकारात्मक) \(x\) मानों का चयन करके, जितना चाहें उतना नकारात्मक और सकारात्मक ले सकता है। और फिर, निष्कर्ष यह है कि परास पूरी वास्तविक रेखा है, जो अंतराल संकेतन का उपयोग करते हुए \((-\infty, +\infty)\) है।
इस तरह का विश्लेषण परिणाम के संदर्भ में सही है, लेकिन तर्क के संदर्भ में यह कमजोर है। सीमा को खोजने के लिए "ग्राफिकल विधि" में वह समस्या है: यह सहज ज्ञान युक्त दृष्टिकोण से आकर्षक है, लेकिन सामग्री के मामले में यह पतली है।
आम तौर पर, यदि संभव हो तो, हमें विश्लेषणात्मक/बीजगणितीय तरीके से प्राथमिकता देनी चाहिए। उदाहरण में, हमें \(x\) के लिए हल करने की आवश्यकता है:
\[x + 3 = y\] \[\Rightarrow \,\, x = y - 3\]तो, क्या \(y\) पर \(x\) को अच्छी तरह परिभाषित करने के लिए कोई प्रतिबंध है? बिल्कुल नहीं, तो फिर, \(y\) पर कोई प्रतिबंध नहीं है और निष्कर्ष यह है कि सीमा पूरी वास्तविक रेखा है।
आप इस लेख की जांच कर सकते हैं जो आप चाहते हैं किसी फ़ंक्शन का डोमेन खोजने का तरीका जानें बजाय।
परास ज्ञात करने के कई अच्छे बीजीय कारण हैं, उनमें से एक यह है कि यह की प्रक्रियाओं का एक भाग है किसी फ़ंक्शन के व्युत्क्रम का पता लगाना .
