डोमेन कैसे खोजें
किसी फ़ंक्शन के डोमेन को खोजना सीखना बीजगणित में एक महत्वपूर्ण कौशल है, क्योंकि यह आपको यह आकलन करने की क्षमता देता है कि फ़ंक्शन को ठीक से परिभाषित किया गया है। या दूसरे शब्दों में, वह क्षेत्र जहां यह फ़ंक्शन संचालित करने के लिए मान्य है
किसी फ़ंक्शन को संचालित करने के लिए यह कहां मान्य है, यह पता लगाने का कार्य उपयोगी है। उदाहरण के लिए, फ़ंक्शन \(f(x) = \sqrt x\) पर विचार करें। हम जानते हैं कि फ़ंक्शन ऐसे मानों को संचालित करता है जैसे कि \(x \ge 0\)। हम ऋणात्मक संख्याओं के साथ काम नहीं कर सकते, क्योंकि हमें \(f(-1) = \sqrt{-1}\) जैसा कुछ मिलेगा, जो अच्छी तरह से परिभाषित नहीं है (कम से कम वास्तविक संख्या के रूप में)
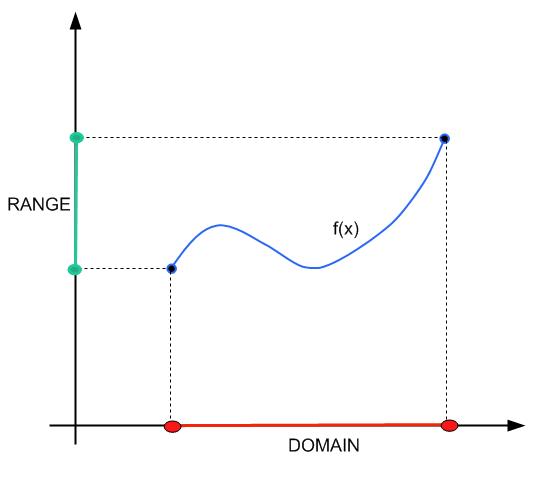
आप हमारे पिछले ट्यूटोरियल को देख सकते हैं जिसमें हमने के बारे में गहराई से बात की थी डोमेन और सीमा . यह ट्यूटोरियल डोमेन खोजने के परिचालन भाग की ओर उन्मुख होगा।
हमें डोमेन खोजने की आवश्यकता क्यों है?
किसी फ़ंक्शन के डोमेन को खोजने की आवश्यकता का कारण यह है कि प्रत्येक फ़ंक्शन में मानों का एक विशिष्ट सेट होता है जहां इसे परिभाषित किया जाता है। सभी कार्यों को वास्तविक रेखा में हर जगह परिभाषित नहीं किया गया है।
वास्तविक रेखा में वह क्षेत्र जहाँ यह है वैध फ़ंक्शन \(f(x)\) के साथ काम करने के लिए, उन मानों के संदर्भ में जो \(x\) ले सकते हैं।
डोमेन खोजने के लिए हमें क्या करना चाहिए?
वास्तव में, कोई एक तरकीब नहीं है जो सभी आकारों में फिट हो। प्रत्येक फ़ंक्शन अलग है और फ़ंक्शन के आधार पर डोमेन को खोजने के लिए विभिन्न रणनीतियों का उपयोग करने की आवश्यकता होती है।
ऐसी दो तकनीकें हैं जिन पर आपको हमेशा ध्यान देना चाहिए:
![]() तकनीक 1
: सुनिश्चित करें कि शून्य से विभाजन हैं।
तकनीक 1
: सुनिश्चित करें कि शून्य से विभाजन हैं।
इसके अलावा, वे बिंदु जो शून्य से विभाजन की ओर ले जाते हैं, उन्हें डोमेन से बाहर करने की आवश्यकता है।
![]() तकनीक 2
: सुनिश्चित करें कि विभाजन नकारात्मक तर्कों के साथ वर्गमूल हैं (जैसे \(\sqrt{-1}\))।
तकनीक 2
: सुनिश्चित करें कि विभाजन नकारात्मक तर्कों के साथ वर्गमूल हैं (जैसे \(\sqrt{-1}\))।
इसके अलावा, वे बिंदु जो ऋणात्मक संख्या के वर्गमूल की ओर ले जाते हैं, उन्हें डोमेन से बाहर करने की आवश्यकता है।
अंततः, इन दो तकनीकों का उपयोग करके आप उन बिंदुओं को हटाने में सक्षम होंगे जो डोमेन में नहीं हैं। वास्तविक रेखा में शेष बिंदु, बस डोमेन का हिस्सा हैं।
तो, ये दो तकनीकें बीजगणितीय रूप से किसी फ़ंक्शन के डोमेन को खोजने का तरीका जानने की समस्या को हल करती हैं। ऐसा करने का एक और तरीका है, यदि उपलब्ध हो तो ग्राफ को देखकर।
उदाहरण 1
फलन \(f(x) = \sqrt{x+4}+3\) का प्रांत ज्ञात कीजिए।
उत्तर:
पहली चीज जो हमें करने की जरूरत है, और वह जगह है जहां डोमेन खोजने में हमारी सफलता निहित है, यह निर्धारित करना है कि संभावित रूप से हमें अमान्य संचालन कहां मिल सकता है, जैसे शून्य से विभाजन, या नकारात्मक वर्गमूल।
फ़ंक्शन \(f(x) = \sqrt{x+4}+3\) के लिए, शून्य से कोई संभावित विभाजन नहीं है, लेकिन एक वर्गमूल है। वैध तर्क होने के लिए, वर्गमूल के अंदर का तर्क गैर-ऋणात्मक होना चाहिए।
इसलिए, \(x\) फ़ंक्शन के डोमेन में होने के लिए, हमारे पास \(x\ge 0\) होना चाहिए। इसका तात्पर्य यह है कि यदि हम अंतराल संकेतन का उपयोग करते हैं तो \(f\) का डोमेन \(\{x: x\ge 0\}\), या \([0, +\infty)\) है।
क्या हमेशा इतना आसान होता है ?? वास्तव में नहीं, यह \(f(x)\) फ़ंक्शन की जटिलता के आधार पर जितना कठिन हो उतना कठिन हो सकता है।
आम तौर पर, हालांकि, आप अपने परीक्षणों और गृहकार्य में जो उदाहरण देखते हैं, वे अपेक्षाकृत सरल होते हैं। आइए हम कठिनाई के मामले में एक पायदान ऊपर जाएं।
उदाहरण 2
अब फंक्शन \(\displaystyle f(x) = \sqrt{\frac{x+4}{x-3}}\) का डोमेन ज्ञात कीजिए।
उत्तर:
यह कार्य थोड़ा अधिक जटिल है और इसके लिए अधिक सावधानीपूर्वक उपचार की आवश्यकता होती है। इस मामले में, हमें शून्य और नकारात्मक वर्गमूल द्वारा संभावित विभाजन दोनों की चिंता करने की आवश्यकता है।
सबसे पहले, शून्य से एक संभावित विभाजन हो सकता है, जब \(x = 3\), जो इंगित करता है कि \(x = 3\) को डोमेन से बाहर रखा जाना चाहिए।
अब, हमें संभावित नकारात्मक वर्गमूल का ध्यान रखना होगा। हमें \(\displaystyle \frac{x+4}{x-3}\) के चिन्ह का आकलन करने की आवश्यकता है। इसके अलावा, हमें इसे गैर-नकारात्मक होने की आवश्यकता है, इसलिए हमें हल करने की आवश्यकता है:
\[\displaystyle \frac{x+4}{x-3} \ge 0\]विभाजन के गैर-ऋणात्मक होने के लिए, हमें या तो अंश और हर दोनों का धनात्मक होना चाहिए, या अंश और हर दोनों का ऋणात्मक होना चाहिए।
दूसरे शब्दों में, हमें \(x+4 \ge 0\) और \(x-3 > 0\), या \(x+4 \le 0\) और \(x-3 < 0\) दोनों की आवश्यकता है।
यह वही है जो \(x \ge -4\) और \(x > 3\), या दोनों \(x \le -4\) और \(x < 3\) दोनों हैं।
और इसे \(x > 3\), या दोनों \(x \le -4\) के रूप में लिखा जा सकता है, जो अंतराल \( (-\infty, -4] \cup (3, +\infty)\) से मेल खाती है।
निष्कर्ष यह है कि फ़ंक्शन \(\displaystyle f(x) = \sqrt{\frac{x+4}{x-3}}\) का डोमेन है:
\[ dom(f) = (-\infty, -4] \cup (3, +\infty)\]जैसा कि आप देख सकते हैं, कठिनाई का स्तर थोड़ा बढ़ गया है, और आप वास्तव में इसे जितना चाहें उतना बढ़ा सकते हैं।
एक परिमेय फलन का डोमेन कैसे खोजें
सबसे पहले, आइए याद करें कि एक परिमेय फलन, रूप के दो बहुपदों का भागफल होता है:
\[f(x) = \frac{p(x)}{q(x)} = \frac{a_0 + a_1 x + ...+ a_m x^m}{b_0 + b_1 x + ...+ b_n x^n}\]उपरोक्त परिमेय फलन के लिए आप प्रांत कैसे ज्ञात करते हैं? हमें अपने नियम का पालन करने की आवश्यकता है: शून्य और नकारात्मक वर्गमूल द्वारा संभावित विभाजन देखें।
इस मामले में, कोई संभावित नकारात्मक वर्गमूल नहीं हैं, लेकिन शून्य से विभाजन हो सकते हैं, जहां हर में बहुपद शून्य है।
निष्कर्ष बहुत सरल है: एक परिमेय फलन का प्रांत उन बिंदुओं को छोड़कर पूरी वास्तविक रेखा है जिसमें हर में बहुपद शून्य है।
उदाहरण 3
का डोमेन खोजें
\[f(x) = \frac{x^2 + x + 1}{x^3 - 6x^2 + 11x - 6}\]उत्तर:
सबसे पहले, हमें यह समझने की आवश्यकता है कि यह एक परिमेय फलन है, क्योंकि आपके अंश और हर में क्रमशः दो बहुपद \(p(x) = x^2 + x + 1\) और \(q(x) = x^3 - 6x^2 + 11x - 6\) हैं।
तो, पहला कदम हर में बहुपद के शून्य को खोजना है, इसलिए हमें हल करने की आवश्यकता है: \[ x^3 - 6x^2 + 11x - 6 = 0\]
उस समीकरण को हल करना मुश्किल है, इसलिए मैं आपको वह वास्तव में \(x^3 - 6x^2 + 11x - 6 = (x-1)(x-2)(x-3)\) दूंगा, इसलिए हमें हल करने की आवश्यकता है:
\[ x^3 - 6x^2 + 11x - 6 = (x-1)(x-2)(x-3) = 0\]जिसका अर्थ है कि हर में बहुपद की जड़ें \(x_1 = 1, x_2 = 2, x_3 = 3\) हैं। निष्कर्ष यह है कि 1, 2 और 3 बिंदुओं को छोड़कर, फ़ंक्शन का डोमेन संपूर्ण वास्तविक रेखा है। अंतराल संकेतन का उपयोग करते हुए, डोमेन \((-\infty, +\infty) \backslash \{1,2,3\}\) है।
किसी फ़ंक्शन का डोमेन ढूँढने के लिए अन्य रणनीतियाँ
शून्य या नकारात्मक वर्गमूल द्वारा संभावित विभाजनों को देखकर किसी फ़ंक्शन के डोमेन को खोजने का विकल्प, जो कि विश्लेषणात्मक तरीका है, ग्राफ को देखकर है।
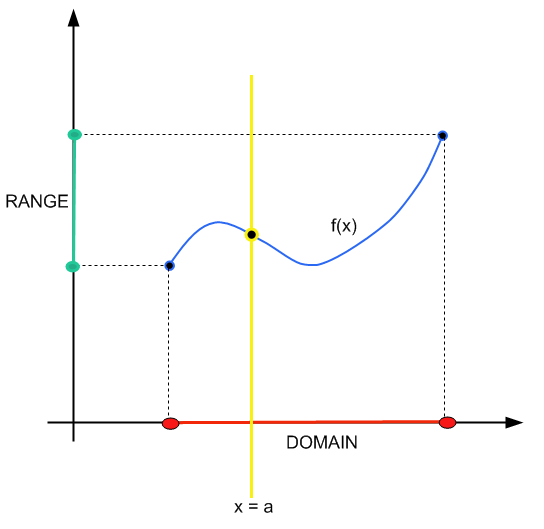
विधि सरल है: आप एक लंबवत रेखा \(x = a\) बनाते हैं। यदि वह लंबवत रेखा एक और केवल एक बिंदु पर फ़ंक्शन के ग्राफ़ को पार करती है, तो \(x = a\) डोमेन से संबंधित है।
छोटा एवं सुन्दर।
अंत में, आप वर्गमूल वाले किसी फलन का प्रांत कैसे ज्ञात करते हैं
यह उन तकनीकों में से एक का मूल है जिसके बारे में हम बात कर रहे हैं, जो संभावित नकारात्मक वर्गमूलों को खोजना है। तो फिर, जब आपके पास एक या अधिक वर्गमूल वाला कोई फ़ंक्शन होता है, तो आप जानते हैं कि यह बहुत संभावना है कि आपके पास संभावित नकारात्मक रूट होगा, और आपको इसका पता लगाने की आवश्यकता है।
हालांकि हमेशा ऐसा नहीं होता है। फ़ंक्शन \(f(x) = \sqrt{x^2}\) के बारे में सोचें। उस फलन का आ वर्गमूल है, लेकिन अंदर तर्क \(x^2\) है, जो ऋणात्मक नहीं हो सकता, इसलिए हमारे पास एक वर्गमूल वाले फलन का मामला है जिसमें ऋणात्मक वर्गमूल नहीं हैं।
