इस निर्धारक कैलकुलेटर के बारे में अधिक।

रैखिक बीजगणित में और मैट्रिस के उपयोग में, एक मैट्रिक्स के निर्धारक का विचार \(A\) सबसे गहरे महत्व की अवधारणा है।

ऐसा इसलिए है क्योंकि इसका उपयोग लगभग हर महत्वपूर्ण ऑपरेशन के साथ बंधा हुआ है जो आप मैट्रिसेस के साथ करना चाहते हैं, जैसे कि मैट्रिसेस की इनवर्टिबिलिटी को सत्यापित करना, अफ़्री या अफ़रिश ।

इसलिए, जहां भी आप मैट्रिस के साथ काम करते समय चारों ओर देखते हैं, आपको एक या दूसरे तरीके से निर्धारक मिलेंगे।इसलिए, उनसे परिचित होना बहुत महत्वपूर्ण है।

यह मैट्रिक्स कैलकुलेटर आपकी मदद कैसे कर सकता है

1. आपको बस अपने मैट्रिक्स को टाइप करने की आवश्यकता है
2. यह एक वर्ग मैट्रिक्स होने की आवश्यकता है, यह एक समान संख्या में पंक्तियों और स्तंभों के साथ एक मैट्रिक्स है
3. बस बटन पर क्लिक करें और कैलकुलेटर आपको सभी चरणों और निर्धारक के अंतिम मूल्य दिखाएगा
4. निर्धारक गणना पर काम करना बेहद श्रमसाध्य और प्रवण त्रुटि हो सकती है।यह कैलकुलेटर आपको उन समस्याओं से अलग करता है

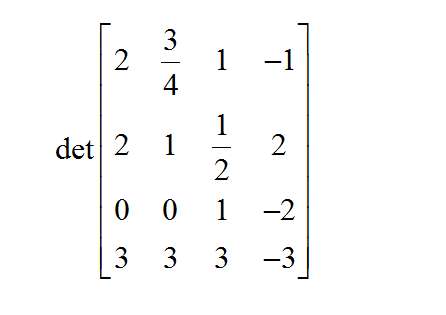
आप एक मैट्रिक्स के निर्धारक की गणना कैसे करते हैं?

यह एक लंबा जवाब हो सकता है, क्योंकि एक मैट्रिक्स के निर्धारक की गणना करने के कई तरीके हैं।आइए हम पहले यह कहें कि निर्धारक केवल वर्ग मैट्रिस के लिए कंप्यूटिंग कर रहे हैं (यह मैट्रिसेस है जिसमें पंक्तियों और स्तंभों की समान संख्या है)।

तो, सबसे छोटा मैट्रिक्स हम एक निर्धारक की गणना कर सकते हैं एक 2x2 मैट्रिक्स है।आइए हम एक सामान्य 2x2 मैट्रिक्स पर विचार करें, जैसा कि नीचे दिखाया गया है:

\[ A = \begin{bmatrix} a & b \\ c & d \end{bmatrix}\]

निर्धारक का सूत्र क्या है?इस मामले में, मैट्रिक्स के निर्धारक \(A\) को केवल \(\det(A) = a d - bc\) के रूप में गणना की जाती है

उदाहरण के लिए, अगर हमारे पास था:

\[ A = \begin{bmatrix} 1 & 2 \\ 1 & 3 \end{bmatrix}\]

मैट्रिक्स का निर्धारक \(A\) \(\det(A) = 1 \cdot 3 - 2 \cdot 1 = 3 - 2 = 1\) होगा।आसान, है ना?

आप 3x3 मैट्रिक्स के निर्धारक को कैसे पाते हैं?

अब, बड़े मैट्रिस के लिए, हम छोटे मैट्रिस के उप-निर्धारण के आधार पर निर्धारक की गणना का निर्माण करते हैं।बस आपको एक स्वाद देने के लिए, आइए एक 3x3 मैट्रिक्स के निर्धारक की गणना करने का एक तरीका देखें।विचार करना

\[ A = \begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end{bmatrix}\]

इस मामले में, मैट्रिक्स 3x3 मैट्रिक्स के निर्धारक \(A\) कई 2x2 निर्धारकों के संचालन के आधार पर गणना की जाती है

\[\det(A) = a \det \begin{bmatrix}e & f \\ h & i \end{bmatrix} - b \det \begin{bmatrix} d & f \\ g & i \end{bmatrix} + c \det\begin{bmatrix} d & e \\ g & h \end{bmatrix}\]

उपरोक्त समीकरणों में मान \(a\), \(b\), \(c\) पिवोट्स की भूमिका निभाते हैं, और एक नकारात्मक संकेत मिल सकता है।एक धुरी का संकेत \((-1)^{i+j}\) है, जहां संबंधित धुरी पंक्ति में है \(i\) और कॉलम \(j\)।

उदाहरण के लिए \(a\) पंक्ति 1, कॉलम 1 में है, इसलिए इसका संकेत \((-1)^{1+1} = (-1)^2 = 1\) (सकारात्मक) है।इसके अलावा, \(b\) पंक्ति 1, कॉलम 2 में है, इसलिए इसका संकेत \((-1)^{1+2} = (-1)^3 = -1\) (नकारात्मक) है, और इसी तरह।

जादू किसी भी पंक्ति या कॉलम को पिवोट्स के रूप में चुनना है।प्रत्येक धुरी में एक संकेत जुड़ा हुआ (सकारात्मक या नकारात्मक) और एक उप-निर्धारण करने वाला होगा, जो इससे संबंधित हैं मैटruguth कोफ़ैक ।

यह उप-निर्धारण, पंक्ति \(i\) और कॉलम \(j\) को हटाने के बाद मूल मैट्रिक्स का वास्तविक निर्धारक है, जो कि पंक्ति में है \(i\) और कॉलम \(j\) में है।

सबसे तार्किक सम्मेलन पिवोट्स के लिए सबसे अधिक शून्य के साथ पंक्ति या कॉलम को चुनने के लिए इंगित करता है, इसलिए यदि संभव हो तो कुछ उप-निर्धारणकर्ताओं की गणना से बचने के लिए।

आप 3x4 मैट्रिक्स के निर्धारक को कैसे पाते हैं?

आप ऐसा नहीं कर सकते।एक 3x4 मैट्रिक्स एक वर्ग मैट्रिक्स नहीं है, और इसलिए, किसी भी निर्धारक की गणना नहीं की जा सकती है।एक निर्धारक की गणना करने के लिए, मैट्रिक्स को समान संख्या में पंक्तियों और स्तंभों की आवश्यकता होती है।

एक 4x4 निर्धारक कैलकुलेटर

बड़े मैट्रिसेस के लिए, कार्यप्रणाली समान है: पिवोट्स के लिए एक पंक्ति या कॉलम चुनें, आदर्श रूप से सबसे अधिक शून्य के साथ।प्रत्येक धुरी के अनुरूप संकेत खोजें, और इसी उप-निर्धारणकर्ताओं को ढूंढें।

तो, आप चार 3x3 निर्धारकों के संचालन में 4x4 मैट्रिक्स के निर्धारक की गणना को कम करते हैं।और बदले में, प्रत्येक 3x3 निर्धारक को कई 2x2 निर्धारकों के संचालन के रूप में पाया जाता है, जिसके लिए हम एक सूत्र जानते हैं।

तो, यह गन्दा असली जल्दी हो सकता है।

एक मैट्रिक्स निर्धारक की गणना का उदाहरण

प्रश्न: निम्नलिखित मैट्रिक्स पर विचार करें:

\[ \begin{bmatrix}1&2&3\\3&1&4\\2&3&8\end{bmatrix}\]

दिए गए मैट्रिक्स के निर्धारक की गणना करें, चरणों को दिखाते हुए।

तमाम: हमें \(3 \times 3\) मैट्रिक्स के निर्धारक की गणना करने की आवश्यकता है जो प्रदान किया गया है।

उप-निर्धारण सूत्र का उपयोग करके हमें मिलता है:

\[ \begin{vmatrix} \displaystyle 1&\displaystyle 2&\displaystyle 3\\[0.6em]\displaystyle 3&\displaystyle 1&\displaystyle 4\\[0.6em]\displaystyle 2&\displaystyle 3&\displaystyle 8 \end{vmatrix} = 1 \cdot \left( 1 \cdot \left( 8 \right) - 3 \cdot \left(4 \right) \right) - 2 \cdot \left( 3 \cdot \left( 8 \right) - 2 \cdot \left(4 \right) \right) + 3 \cdot \left( 3 \cdot \left( 3 \right) - 2 \cdot \left(1 \right) \right)\] \[ = 1 \cdot \left( -4 \right) - 2 \cdot \left( 16 \right) + 3 \cdot \left( 7 \right) = -15\]

निष्कर्ष : ऊपर दिखाए गए गणनाओं के आधार पर, यह पाया जाता है कि मैट्रिक्स का निर्धारक \(\det A = \displaystyle -15\) है।

अन्य उपयोगी मैट्रिक्स कैलकुलेटर जो आप उपयोग कर सकते हैं

हाथ से किए गए मैट्रिक्स गणना श्रम-गहन हैं, इसलिए आप हमारे रैखिक बीजगणित सॉल्वरों का लाभ उठा सकते हैं।

सबसे पहले, आप इस व्युत्क्रम मैट्रिक्स कैलकुलेटर का उपयोग कर सकते हैं ताकि एक मैट्रिक्स दिखाने वाले चरणों के व्युत्क्रम की गणना की जा सके, और आप इसे या तो कर सकते हैं तंग , या उपयोग करके Rref में कमी ।