फैक्टर कैसे करें
कारक बनाना सीखना सबसे महत्वपूर्ण कौशलों में से एक है जिसे आप सीख सकते हैं। फैक्टरिंग में इतने सारे अनुप्रयोग हैं, कि आपको इसके बारे में सब कुछ जानने के लिए समय निकालने में खुशी होगी।
फैक्टरिंग आम तौर पर कुछ ऐसा होता है जिसे हम मान लेते हैं, और विभिन्न गुणों पर आधारित होते हैं, जैसे कि कम्यूटेटिव, एसोसिएटिव और डिस्ट्रीब्यूटिव प्रॉपर्टी। वे गुण आपको सुविधाजनक तरीके से घूमने और शब्दों को समूहबद्ध करने की अनुमति देते हैं।
कम्यूटेटिव, साहचर्य और वितरणात्मक संपत्ति के बारे में एक त्वरित ताज़गी। वास्तविक संख्या \(x\), \(y\) और \(z\) के लिए, हमारे पास निम्नलिखित गुण हैं
(जोड़ की साहचर्यता) \((x+y)+z = x+(y+z)\)
जोड़ की क्रमपरिवर्तन) \( x + y = y + x\)
(वितरक संपत्ति) \( x \cdot (y+z) = x \cdot y + x \cdot z\)
जहां \(+\) और \(\cdot\) क्रमशः वास्तविक संख्याओं का योग और गुणनफल हैं।
यह जानना क्यों उपयोगी है कि कारक कैसे बनाया जाता है?
कई कारण हैं, लेकिन महत्वपूर्ण कारणों में से एक यह है कि फैक्टरिंग हमें समीकरणों को हल करने का एक आसान तरीका देता है। वास्तव में, फैक्टरिंग वह तरीका है जिससे हमें समीकरणों को हल करना होता है।
उदाहरण के लिए, उस समीकरण पर विचार करें जहां हम \(x\) के लिए हल करने का प्रयास कर रहे हैं:
\[\large xy +xz = 0\]हम इसके बारे में कैसे जाते हैं? खैर, हम वितरण संपत्ति का उपयोग प्राप्त करने के लिए कर सकते हैं:
\[\large x y + x z = x(y+z) = 0\]इसलिए, इस अंतिम अभिव्यक्ति \( x(y+z) = 0\) के साथ हमारे पास फैक्टरिंग का एक उदाहरण है। वास्तव में, हमने प्रारंभिक व्यंजक \(xy+xz\) लिया और हमने इसे \( x(y+z)\) में विभाजित किया।
तो, अब हमें एक आसान समीकरण को हल करने की आवश्यकता है, जो कि \( x(y+z) = 0\) है। यह आसान क्यों है? ऐसा इसलिए है क्योंकि अब हम जानते हैं कि उत्पाद \( x(y+z)\) शून्य के बराबर है, तो कारकों में से एक को शून्य के बराबर होना चाहिए।
इसलिए, यदि हम उस \(y+z = \not 0\) को जानते हैं, तो हम जानते हैं कि हमारे पास वह \(x = 0\) होना चाहिए।
सबक
: फैक्टरिंग का एक फायदा यह है कि एक समीकरण को शून्य के बराबर कारकों के गुणन के रूप में लिखा जा सकता है। फिर, कारकों में से कम से कम एक शून्य होना चाहिए।
उदाहरण के लिए, जब हमें निम्नलिखित समीकरण में \(x\) के लिए हल करने की आवश्यकता होती है:
\[\large 5x + 3x = 0\]जब हम ऐसा करते हैं तो हमें एहसास नहीं होता कि हम वास्तव में फैक्टरिंग कर रहे हैं
\[\large 5x + 3x = (5+3)x = 8x = 0\]इसलिए हमने अपने समीकरण को शून्य के बराबर कारकों के उत्पाद में घटा दिया है: \(8x = 0\)। चूंकि कारकों में से एक \(8\) शून्य के बराबर नहीं है, तो एकमात्र संभावित समाधान \(x = 0\) है।
दूसरे शब्दों में
: यदि आप जानते हैं कि कैसे कारक बनाना है, तो आप निश्चित रूप से जानेंगे
समीकरणों को कैसे हल करें
.
बहुपदों का गुणनखंड कैसे करें
समीकरणों को हल करने के लिए इसकी उपयोगिता के संदर्भ में फैक्टरिंग की भूमिका अब तक स्पष्ट होनी चाहिए। एकमात्र समस्या यह है कि एक सामान्य, एकल रणनीति नहीं है जिसका उपयोग सभी संभावित बीजीय अभिव्यक्तियों को कारक बनाने के लिए किया जा सकता है।
इसलिए, आम तौर पर, हमें अपेक्षाकृत सरल अभिव्यक्तियों को कारक करने में खुशी होगी, लेकिन आदर्श रूप से, हम यह जानना चाहेंगे कि हम अधिक से अधिक अभिव्यक्तियों को कैसे कारक बना सकते हैं।
संतुलन एक बहुत ही सामान्य वर्ग के भावों के साथ पहुँचा जाता है, जिसे हम कई बार, बहुत व्यवस्थित रूप से कारक बना सकते हैं। वह वर्ग बहुपदों का वर्ग है। उदाहरण के लिए, अभिव्यक्ति
\[\large 2x^2 + 5x + 3\]घात 2 का बहुपद है। या नीचे दिया गया व्यंजक
\[\large x^3 - 3x^2 + 4x+2\]घात 3 का बहुपद है।
सामान्य तौर पर, फॉर्म की अभिव्यक्ति
\[\large a_n x^n + a_{n-1}x^{n-1} + ... + a_1 x + a_0\]घात \(n\) का बहुपद है। स्वाभाविक रूप से, व्यंजक जितना सरल होगा, सरल करना उतना ही आसान होगा, इसलिए हमें पहले द्विघात व्यंजकों को गुणनखंड करने का तरीका सीखने का प्रयास करना चाहिए। यह डिग्री दो का बहुपद है।
उदाहरण 1
निम्नलिखित द्विघात व्यंजक का गुणनखंड करें
\[\large x^2 + x - 2\]उत्तर:
यह उदाहरण आपको जानबूझकर दिखाएगा कि ऊपर दिए गए की तरह सरलतम अभिव्यक्ति को भी कारक बनाना मुश्किल हो सकता है। आप इसे कारक बनाने के लिए क्या करेंगे?
क्या होगा यदि मैं आपसे कहूं, आपको शून्य जोड़ने की आवश्यकता है? यह बहुत ही हास्यास्पद है, है ना? आइए देखते हैं:
\[\large x^2 + x - 2 = x^2 + x + 0 - 2 \]क्या आप उपरोक्त से सहमत हैं? मैंने अभी-अभी \(0\) जोड़ा है। कुछ नहीं बदला है। लेकिन, क्या होगा अगर मैं आपको बता दूं कि \(0 = 2x - 2x\)? तो फिर
\[\large x^2 + x - 2 = x^2 + x + 0 - 2 = x^2 + x + (2x - 2x) - 2 \]सब एक जैसे! यह काम करता है, क्योंकि मैंने शून्य जोड़ा है, इसलिए कुछ भी नहीं बदलता है। लेकिन अब हम इसका विस्तार करते हैं और इसे समूहित करते हैं:
\[\large x^2 + x - 2 = x^2 + x + 0 - 2 \] \[\large = x^2 + x + (2x - 2x) - 2 \] \[ \large = x^2 + x - 2x + 2x - 2 \] \[\large = x^2 + (x - 2x) + 2x - 2 \] \[\large = x^2 - x + 2x - 2 \] \[\large = x(x-1) + 2(x-1)\] \[\large = (x+2)(x-1)\]तो, अंत में, \(x^2 + x - 2 = (x+2)(x-1)\)। मुश्किल? शायद, लेकिन ऐसा करने का यह एक तरीका है। इसे करने का एक चतुर तरीका होने के बावजूद, हम अधिक व्यवस्थित तरीके को पसंद करेंगे।
गुणनखंड एक द्विघात बहुपद
चतुर तरकीबें अच्छी हैं, और वह सब, लेकिन आमतौर पर हम एक व्यवस्थित दृष्टिकोण पसंद करेंगे, जो कभी विफल न हो। द्विघात बहुपद (डिग्री 2 के बहुपद) के लिए, फ़ैक्टरिंग के साथ आगे बढ़ने का एक व्यवस्थित तरीका है:
चरण 1
: द्विघात व्यंजक \(ax^2 + bx + c\) को देखते हुए, हम पहले समीकरण को हल करते हैं
चरण 2
: यदि उपरोक्त समीकरण के हल (मूल) वास्तविक हैं (भले ही केवल एक मूल हो), तो हम उन मूलों को \(x_1\) और \(x_2\) कहते हैं। इन जड़ों के साथ, हमें निम्नलिखित कारक मिलते हैं:
इसलिए समाधान \(x_1\) और \(x_2\) कारकों को पूरी तरह से निर्धारित करते हैं।
स्वाभाविक रूप से इस मामले में, जैसा कि अपेक्षित था, द्विघात समीकरण को हल करना द्विघात समीकरण के गुणन के साथ कसकर जुड़ा हुआ है।
उदाहरण 2
निम्नलिखित द्विघात समीकरण का गुणनखंड करें
\[\large x^2 - 4x + 3\]इसकी जड़ों की गणना करके।
उत्तर:
हम संबंधित द्विघात समीकरण को हल करके शुरू करते हैं:
\[\large x^2 - 4x + 3 = 0\]प्रसिद्ध और प्रसिद्ध . का उपयोग करना द्विघात सूत्र :
\[\large\displaystyle x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \] \[\large\displaystyle = \frac{-(-4) \pm \sqrt{(-4)^2 - 4(1)(3)}}{2(1)} \] \[\large\displaystyle = \frac{4 \pm \sqrt{16 - 12}}{2} \] \[\large\displaystyle = \frac{4 \pm \sqrt{4}}{2} \] \[\large\displaystyle = \frac{4 \pm 2}{2} \]जिसका अर्थ है कि समाधान (जड़) \(x_1 = 1\) और \(x_2 = 1\) हैं। फिर, द्विघात व्यंजक \(x^2 - 4x + 3\) को निम्नानुसार गुणनखंडित किया जा सकता है:
\[\large x^2 - 4x + 3 = a(x - x_1)(x - x_2) = (x-1)(x-3) \]ध्यान दें कि इस स्थिति में \(x^2\) पद को गुणा करने वाला पद 1 है, तो इस स्थिति में \(a = 1\)।
2 . से अधिक घात वाले बहुपदों का गुणनखंडन
इसलिए, द्विघात बहुपदों का गुणनखंड करने के लिए मैं संबंधित द्विघात समीकरण के मूलों की गणना करता हूं। मैं उच्च डिग्री के बहुपदों का गुणनखंड कैसे करूं ?? बिल्कुल उसी विधि का उपयोग करना .
चरण 1:
बहुपद व्यंजक \(a_n x^n + a_{n-1}x^{n-1} + ... + a_1 x + a_0\) को देखते हुए, हम पहले समीकरण को हल करते हैं
\[\large a_n x^n + a_{n-1}x^{n-1} + ... + a_1 x + a_0 = 0\]
चरण 2:
यदि उपरोक्त समीकरण के हल (मूल) वास्तविक हैं (भले ही वे दोहराए गए हों), तो हम उन मूलों को \(x_1\), \(x_2\), ..., \(x_n\) कहते हैं। इन जड़ों के साथ, हमें निम्नलिखित कारक मिलते हैं:
\[\large a_n x^n + a_{n-1}x^{n-1} + ... + a_1 x + a_0 = a_n(x - x_1)(x - x_2)\cdots (x - x_n)\]
तो, ऐसा प्रतीत होता है कि घात 2 के बहुपद का गुणनखंड करना उतना ही सरल है जितना कि घात 10 के बहुपद का गुणनखंड करना। सैद्धांतिक रूप से, उत्तर हां है।
एकमात्र समस्या यह है कि कोई सरल, निकट बीजगणितीय सूत्र नहीं है जो डिग्री 5 या उससे अधिक के बहुपद समीकरण के लिए जड़ों को हल कर सके।
कभी-कभी, हम ग्राफ को देखकर या कैलकुलेटर का उपयोग करके भी उच्च डिग्री समीकरणों को हल कर सकते हैं। उदाहरण के लिए, नीचे दिए गए ग्राफ़ की जाँच करें:
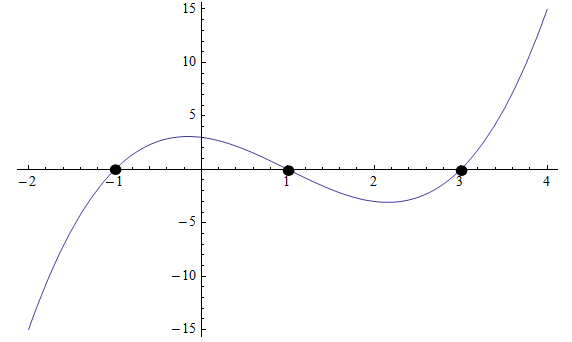
आलेखीय रूप से, हम देख सकते हैं कि बहुपद x-अक्ष को तीन बिंदुओं पर काटता है: \(x_1 = -1\), \(x_2 = 1\) और \(x_3 = 3\), इसलिए ये मूल हैं।
तो, हम जानते हैं कि बहुपद \(p(x) = a(x+1)(x-1)(x-3)\) के रूप में होना चाहिए। स्थिरांक \(a\) जानने के लिए हमें एक और बिंदु जानना होगा।
फैक्टरिंग के बारे में अधिक
हम केवल फैक्टरिंग की अवधारणा के साथ सतह को खरोंच रहे हैं, हालांकि सामान्य अभिव्यक्तियों के लिए जितना किया जा सकता है उससे कहीं अधिक नहीं है। सबसे अच्छा हम यह कर सकते हैं कि कारक बहुपदों के लिए एक व्यवस्थित दृष्टिकोण दिया जाए।
लेकिन, कारक बहुपदों के लिए एक सामान्य उपचार होना कोई छोटी बात नहीं है, और एक बहुपद को गुणन करने के लिए जड़ों का उपयोग करने का विचार बीजगणित के मौलिक प्रमेय से कम नहीं है। तो, कम से कम शीर्षक से, आप बता सकते हैं कि यह छोटा नहीं है।
फैक्टरिंग जनरल एक्सप्रेशन
सामान्य अभिव्यक्तियों को कारक बनाने के लिए कोई सामान्य नियम नहीं हैं। हमें कान से खेलने और अभिव्यक्ति की संरचना का फायदा उठाने की कोशिश करने की जरूरत है। कभी-कभी हम कारक कर सकते हैं, कभी-कभी हम नहीं कर सकते। यह सब अभिव्यक्ति पर निर्भर करता है। एकमात्र सामान्य नियम समूह बनाने का प्रयास करना है और सामान्य कारकों को खोजने का प्रयास करना है ताकि आगे समूह और सरल बनाया जा सके।
ग्रुपिंग द्वारा फैक्टर कैसे करें
यह पहला उदाहरण है जो हमने किया। कहो आपके पास है:
\[\large x^2 - x + 2x - 2 \]इसलिए हम प्राप्त करने के लिए पहले दो पदों और अंतिम दो पदों को समूहित करते हैं:
\[\large (x^2 - x) + (2x - 2) \]और इनमें से प्रत्येक समूह को इस प्रकार विभाजित किया जा सकता है
\[\large x(x - 1) + 2(x - 1) \]और अब हमारे पास दो पद हैं जिनका एक उभयनिष्ठ गुणनखंड \(x-1\) है, इसलिए हम इसका गुणनखंड इस प्रकार करते हैं
\[\large (x+2)(x - 1) \]कभी-कभी कारकों को खोजने के लिए कैलकुलेटर का उपयोग करना अधिक व्यावहारिक होता है। आप हमारे का उपयोग कर सकते हैं द्विघात समीकरण सॉल्वर द्विघात व्यंजक के गुणनखंड ज्ञात करना।
ध्यान दें कि ऐसी कई तकनीकें हैं जो आपकी मदद कर सकती हैं जब आपको किसी व्यंजक को उसकी संरचना के आधार पर कारक बनाने की आवश्यकता होती है। उन्हीं में से एक है की विधि समूह द्वारा कारक जो, जब यह काम करता है, सरलीकरण प्रक्रिया को पूरी तरह से सरल बना सकता है।