लघुगणक समीकरणों को हल करना
लघुगणितीय समीकरणों को हल करना कुछ ऐसा है जो आपको बीजगणितीय प्रक्रियाओं से निपटने के दौरान अक्सर करना होगा, और उनसे निपटने के लिए एक ठोस रणनीति विकसित करने के लायक है।
आप इस ट्यूटोरियल में क्या सीखेंगे, यह मुख्य रणनीतियों है जो आपको लॉगरिदमिक समीकरणों को हल करने के लिए पालन करने की आवश्यकता है।
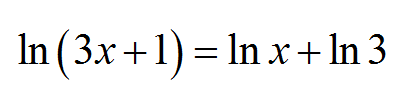
लॉगरिदमिक समीकरण क्या है?
पहली चीज जिसे हमें परिभाषित करना है कि लॉगरिदमिक समीकरण क्या है।
एक लॉगरिदमिक समीकरण एक समीकरण है जिसमें कम से कम एक अज्ञात चर शामिल होता है, जहां एक लघुगणक अभिव्यक्ति समीकरण के कम से कम एक तरफ दिखाई देती है
।
एक लॉगरिदमिक समीकरण का एक उदाहरण है
\[\ln x = 2\ln x - \ln 3\]या भी
\[ \ln(3x-1) - \ln(2x + 1) = 1\]
ध्यान दें कि एक लॉगरिदमिक समीकरण में एक से अधिक अज्ञात हो सकते हैं, उदाहरण के लिए
लघुगणक समीकरणों को हल करने के लिए रणनीतियां
पहला अस्वीकरण यह है कि एक लॉगरिदमिक समीकरण को हल करने के लिए कोई बुलेट-सबूत तरीके नहीं हैं, न ही उस मामले के लिए एक सामान्य समीकरण।इसका कारण यह है कि सभी विधियां समीकरण में एक निश्चित संरचना मानते हैं, जो कि सभी समीकरणों में जरूरी नहीं है।
इसलिए, हम लॉगरिदमिक समीकरणों को हल करने का तरीका नहीं ढूंढ सकते हैं, क्योंकि कोई भी तरीका नहीं है जो सभी संभावित मामलों से निपटेंगे।
फिर भी, अनुसरण करने के लिए कुछ रणनीतियां हैं जो आपको समीकरण के माध्यम से जाने और समाधान खोजने का सबसे अच्छा मौका देगी, अगर कोई मौजूद है।
सबसे पहले, सभी लॉगरिदमिक अभिव्यक्ति को एक लॉगरिदमिक अभिव्यक्ति में समूहित करने का प्रयास करें।
यह आमतौर पर सबसे आम का उपयोग करके हासिल किया जाता है लॉग नियम , जो आपको एक लॉगरिदमिक अभिव्यक्ति को कॉम्पैक्ट करने की अनुमति देता है, यदि अभिव्यक्ति की संरचना इसे अनुमति देती है।
दूसरा, एक बार लॉगरिदमिक अभिव्यक्तियों को जितना संभव हो सके कॉम्पैक्ट किया गया है, आप आमतौर पर समानता के दोनों किनारों पर घातीय कार्य को लागू करके उनसे छुटकारा पाएंगे।
यह अंतिम चरण, उम्मीद है कि, तस्वीर से सभी लॉगरिदम को हटा देगा, और यह आपको अज्ञात (ओं) के लिए हल करने की अनुमति देगा।
तो, दूसरे शब्दों में, एक लॉगरिदमिक समीकरण को हल करने में लॉगरिदमिक अभिव्यक्तियों को समूहबद्ध करना शामिल है, जो उन्हें घातीय लागू करके समाप्त कर देता है, और फिर समीकरण को नियमित समीकरण के रूप में हल करता है।
जाहिर है, जब आप लॉगरिदम से छुटकारा पा चुके हैं, तो आप एक समीकरण का सामना करते हैं जिसमें अपनी चुनौतियां हो सकती हैं।
लघुगणक समीकरणों के विभिन्न उदाहरणों को हल करना
वास्तव में उन्हें सुलझाने की तुलना में समीकरणों को हल करने का तरीका सीखने का कोई बेहतर तरीका नहीं है:
उदाहरण 1:
निम्नलिखित समीकरण हल करें:
\[\large 4 \log(\sqrt x) = \log(6x-1)\]उत्तर:
आइए रणनीतियों का पालन करें।विचार लॉगरिदमिक अभिव्यक्तियों को जितना संभव हो सके कॉम्पैक्ट करना है।यह एक निर्णय कॉल है, क्योंकि मुख्य विचार अनिवार्य रूप से लॉगरिदम से छुटकारा पाने के लिए है।
लॉग नियमों का उपयोग करके हम लॉगरिदम के अंदर "4" डाल सकते हैं
\[\large 4 \log(\sqrt x) = \log(6x-1)\] \[\large \Rightarrow \log((\sqrt x)^4) = \log(6x-1)\] \[\large \Rightarrow \log(x^2) = \log(6x-1)\]अब जब लॉगरिदमिक अभिव्यक्ति यथासंभव संकुचित हैं, तो हमें लॉगरिदम से छुटकारा पाने की आवश्यकता है।
ऐसा करने का एक तरीका समानता के प्रत्येक पक्ष को घातीय कार्य \(10^x\) लागू करना है।उससे मेरा मतलब क्या है???
खैर, आपके पास समानता में दो पक्ष हैं।चूंकि दोनों पक्ष समान हैं, जब फ़ंक्शन \(10^x\) के तर्क के रूप में उपयोग किया जाता है, तो इसे समानता को संरक्षित करना चाहिए।तो हमारे पास
\[\large \log(x^2) = \log(6x-1)\] \[\large \Rightarrow 10^{\log(x^2)} = 10^{\log(6x-1)}\] \[\large \Rightarrow x^2 = 6x-1\]क्योंकि हम जानते हैं कि \(10^{\log a} = a\), जो मूल लॉग नियमों में से एक है।
तो अब जब हमने लॉगरिदम को समाप्त कर दिया है, तो हम दिए गए समीकरण को हल कर सकते हैं:
\[\large x^2 = 6x-1\] \[\large \Rightarrow x^2 - 6x + 1 = 0\] \[\large \Rightarrow x = \frac{-(-6) \pm \sqrt{(-6)^2-4(1)(1)}}{2(1)}\] \[\large \Rightarrow x = \frac{6 \pm \sqrt{36-4}}{2}\] \[\large \Rightarrow x = \frac{6 \pm \sqrt{32}}{2}\] \[\large \Rightarrow x = \frac{6 \pm 4\sqrt{2}}{2}\] \[\large \Rightarrow x = 3 \pm 2\sqrt 2\]तो फिर \(x_1 = 3 + 2\sqrt 2\) और \(x_2 = 3 - 2\sqrt 2\)।तकनीकी रूप से, आपको यह जांचने की आवश्यकता है कि ये दोनों मूल समीकरण के समाधान हैं, इसलिए यह सुनिश्चित करने के लिए कि वे लॉगरिदमिक अभिव्यक्तियों के डोमेन से संबंधित हैं।
इस मामले में, \(x_1 = 3 + 2\sqrt 2\) और \(x_2 = 3 - 2\sqrt 2\) दोनों मूल समीकरण के समाधान हैं।
उदाहरण 2:
निम्नलिखित लॉगरिदमिक समीकरण हल करें:
\[\large \ln 5 - \ln(6-x) = \ln x\]उत्तर:
लॉग नियमों का उपयोग करके हम लॉग अभिव्यक्तियों को कॉम्पैक्ट कर सकते हैं, हम इसे प्राप्त करते हैं
\[\large \ln 5 - \ln(6-x) = \ln x\] \[\large \displaystyle \Rightarrow \ln\left(\frac{5}{6-x}\right) = \ln x\] \[\large \displaystyle \Rightarrow e^{\ln\left(\frac{5}{6-x}\right)} = e^{\ln x}\] \[\large \displaystyle \Rightarrow \frac{5}{6-x} = x\]क्योंकि हम जानते हैं कि \(e^{\ln a} = a\), जो मूल लॉग नियमों में से एक है।
इसलिए, अब हमने लॉगरिदम को समाप्त कर दिया है, हम समीकरण को हल कर सकते हैं जिसे हमने छोड़ा है:
\[\large \displaystyle \frac{5}{6-x} = x\] \[\large \displaystyle \Rightarrow 5 = x(6-x)\] \[\large \displaystyle \Rightarrow 5 = 6x - x^2\] \[\large \displaystyle \Rightarrow x^2 -6x + 5 = 0\] \[\large \displaystyle \Rightarrow (x-1)(x-5) = 0\]तो फिर \(x_1 = 1\) और \(x_2 = 5\)।आइए इन मानों को मूल समीकरण में प्लग करें ताकि यह देखने के लिए कि वे वास्तव में समाधान हैं:
\(x_1 = 1\) के लिए:
जो समान है:
\[\large \ln 5 - \ln(5) = 0\]जो सच है, इसलिए समीकरण रखता है।
\(x_1 = 5\) के लिए:
जो समान है:
\[\large \ln 5 - \ln(1) = \ln(5)\]जो सच है, इसलिए समीकरण रखता है।
इसलिए, समीकरण के समाधान \(x_1 = 1\) और \(x_2 = 5\) हैं।
लॉगरिदमिक समीकरणों को हल करने के बारे में अधिक जानकारी
एक बात यह है कि छात्र सबसे अधिक चिंतित हैं कि आप एक समीकरण में लॉग से कैसे छुटकारा पा सकते हैं।लेकिन हमने देखा है कि वास्तव में आसान हिस्सा है।वास्तव में बीजगणितीय रूप से अभिव्यक्ति को काम करना कठिन है ताकि लॉग हटा दिए जा सकें।
इससे विभिन्न अड्डों से निपटने के तरीके का सवाल उठता है, जिसके लिए अपने अनुच्छेद की आवश्यकता होती है।
विभिन्न आधारों के साथ लघुगणकीय समीकरणों को हल करना
उपर्युक्त उदाहरणों में हमने केवल \(\log\) (बेस 10 के साथ लघुगणक) और \(\ln\) (बेस \(e\) के साथ लघुगणक) के साथ निपटाया।जब आप एक अलग आधार के साथ एक लॉगरिदम होते हैं तो आप इसे कैसे करते हैं, जैसे \(\log_a\) ???
उत्तर सरल है: एक अलग बेस के साथ लॉगरिदम को खत्म करने के लिए, \(\log_a\) कहें जिसमें बेस \(a\) है, हम बस घातीय फ़ंक्शन \(a^x\) का उपयोग करते हैं।सरल सही ??
दरअसल, लॉगरिदम को खत्म करना लॉग समीकरणों को हल करने का आसान हिस्सा है।प्रक्रिया का कठिन हिस्सा एक ऐसे रूप में लॉगरिदमिक अभिव्यक्तियों को समूहबद्ध करना और कॉम्पैक्ट करना है जिसे आप उन्हें खत्म करते हैं।
आप इस बारे में और जान सकते हैं कि लॉगरिदमिक फ़ंक्शन कैसे देखकर काम करता है इसके ग्राफ के गण और पढ़ाई मौलल लॉग नायम ।