Correlation Coefficient Calculator
Instructions: You can use this step-by-step Correlation Coefficient Calculator for two variables X and Y. All you have to do is type your X and Y data, either in comma or space separated format (For example: "2, 3, 4, 5", or "3 4 5 6 7").
Correlation Coefficient Calculator
The correlation coefficient calculated above corresponds to Pearson's correlation coefficient. The requirements for computing it is that the two variables X and Y are measured at least at the interval level (which means that it does not work with nominal or ordinal variables).
The formula for Pearson's correlation coefficient is:
\[r =\frac{n \sum_{i=1}^n x_i y_i - \left(\sum_{i=1}^n x_i \right) \left(\sum_{i=1}^n y_i \right) }{\sqrt{n \sum_{i=1}^n x_i^2 - \left( \sum_{i=1}^n x_i \right)^2} \sqrt{n \sum_{i=1}^n y_i^2 - \left( \sum_{i=1}^n y_i \right)^2} }\]or equivalently
\[r = \frac{\sum_{i=1}^n x_i y_i - \frac{1}{n}\left(\sum_{i=1}^n x_i \right) \left(\sum_{i=1}^n y_i \right) }{\sqrt{\sum_{i=1}^n x_i^2 - \frac{1}{n}\left( \sum_{i=1}^n x_i \right)^2} \sqrt{\sum_{i=1}^n y_i^2 - \frac{1}{n}\left( \sum_{i=1}^n y_i \right)^2}} = \frac{SS_{XY}}{\sqrt{SS_{XX}\cdot SS_{YY} }}\]If you have two or more variables, you could use our correlation matrix calculator . Also, if the data for the variables \(X\) and \(Y\) does not meet the parametric assumptions for Pearson's correlation, then you should use this Spearman's correlation calculator instead.
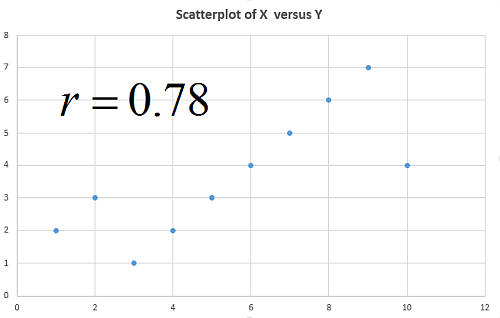
Correlation and Regression
Correlation and regression are not the same thing, though they are tightly related concepts. Correlation analysis corresponds to the calculation of the correlation coefficient, which is a value that ranges from -1 to 1, that assess the degree of linear association between two variables.
The closer in absolute value the correlation gets to 1, the tighter the linear association between the two variables is. Close to 1 indicates a tight positive linear association, and close to -1 indicates a tight negative association
The process of conducting a correlation analysis often also involves constructing a scatterplot, in order to confirm the information yielded by the coefficient coefficient.
Once we have confirmed that the correlation is close to 1 in absolute value that the scatterplot shows a reasonably tight linear pattern, then we can run a linear regression analysis, in order to quantitatively assess the effect of the independent variable X on the dependent variable Y.
Can I use z-scores to compute the correlation coefficient
Certainly! You have seen z-scores everywhere in Statistics and naturally, you wonder if you can compute the correlation with z-scores . You can definitely do it, and in fact, it is the customary way of doing it in Social Sciences stats.
Other calculators similar to this correlation calculator
Also, there is the concept of multiple correlation coefficient , when you have more than one predictor, which is obtained by computing the correlation between the observed \(Y\) values and the predicted values \(\hat Y\) by the regression.